Одной из характерных тенденций развития аэрокосмической отрасли является постоянное расширение требований к техническим характеристикам, функциональным возможностям летательных аппаратов (как атмосферных, так и космических) и их подсистемам. Данная тенденция является естественным процессом, вызванным развитием науки и технологическим прогрессом. Однако стремление к увеличению возможностей аэрокосмической техники, выражающееся в расширении функциональных возможностей, областей полета, приводит к необходимости значительного усложнения как конструкции аппаратов в целом, так и их отдельных подсистем.
Например, если на заре развития космических систем объем информации, предаваемой на землю, и функциональные возможности аппаратов были крайне ограниченными, то в настоящее время объем предаваемой информации вырос в тысячи раз, современные космические аппараты способны выполнять крайне широкий круг задач – фото- и видеосъемку из космоса, ретрансляционные функции, экологическое, боевое и политическое применение и т.д. Соответственно, достигнуть таких функциональных возможностей и обеспечить их дальнейшее расширение можно только значительным усложнением конструкции подобных систем. Это приводит к появлению большого класса задач, связанных с передачей, сжатием, шифрованием, фильтрацией больших объемов информации, распознавания объектов на изображениях (в том числе снятых, в разных длинах волн), полученных со спутника, дистанционного управления объектами.
Важной и все более актуальной проблемой является вопрос повышения безопасности полетов аэрокосмических систем. Создание и развитие сложных инженерных систем современного уровня, какими являются летательные аппараты, требует в настоящее время подхода основанного на методах многодисциплинарного анализа и проектирования [1, 4, 5]. Прогресс в вычислительных методах и оборудовании требует применения (создания) новых алгоритмических процедур основанных на распараллеливании процессов. Для решения задач многодисциплинарной оптимизации в настоящее время весьма актуальным является изучение и разработка методов, основанных на применении систем с искусственным интеллектом (нейронные сети, эволюционные алгоритмы и методы нечеткой логики) [7, 8].
Можно условно выделить четыре основных подхода к построению интеллектуальных систем – это нейронные сети, нечеткая логика (fuzzy logic), экспертные системы, эволюционные алгоритмы. Отличительной чертой всех этих подходов является то, что в отличие от стандартных детерминированных методов они используют идеи моделирования работы мозга, механизма принятия решений человеком и принципы живой природы (эволюция, естественный отбор). В то же время каждый из этих методов обладает своими особенностями.
Искусственные нейронные сети – это математический метод имитации процессов и явлений, основанный на моделировании работы мозга человека и позволяющий воспроизводить чрезвычайно сложные зависимости. Важной чертой НС является то, что в силу конструктивных особенностей они позволяют успешно решать задачи с большим количеством переменных, не требуя большого количества вычислительных ресурсов (по сравнению со стандартными детерминированными методами).
Целью работы является определение аэродинамических характеристик высокоскоростных летательных аппаратов с помощью искусственных нейронных сетей.
Биологический нейрон
Рассмотрим достаточно кратко устройство и принцип функционирования биологического нейрона. Нейрон является особой биологической клеткой, которая обрабатывает информацию (рис. 1). Она состоит из тела клетки (cell body) или сомы (soma) и двух типов внешних древоподобных ветвей: аксона (axon) и дендритов (dendrites). Тело клетки включает ядро (nucleus), которое содержит информацию о наследственных свойствах и плазму, обладающую молекулярными средствами для производства необходимых нейрону материалов. Нейрон получает импульсные сигналы от других нейронов через дендриты (приемники) и передает сигналы сгенерированные телом клетки вдоль аксона (передатчик). Аксон в конце разветвляется на волокна, на окончаниях которых находятся синапсы (synapses). Синапс – единственный путь, с помощью которого нейроны могут сообщаться друг с другом и обеспечивать все основные проявления активности нервной системы. В синапсы входят предсинаптическая часть или синаптическое окончание, синаптическая щель, разделяющая две клетки и постсинаптическая часть [6].
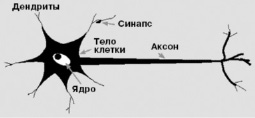
Рис. 1. Биологический нейрон
Когда импульс достигает синаптического окончания, высвобождаются определенные химические вещества, называемые нейротрансмиттерами. Нейротрансмиттеры диффундируют через синаптическую щель, возбуждая или затормаживая в зависимости от типа синапса способность нейрона – приемника генерировать электрические импульсы. Результативность синапса может настраиваться проходящими через него сигналами, так что синапсы могут обучаться в зависимости от активности процессов, в которых они участвуют. Эта зависимость от предыстории действует как память, которая, возможно, ответственна за память человека. Нейроны взаимодействуют посредством короткой серии импульсов, как правило, продолжительностью несколько мс. Сообщения передаются посредством частотно-импульсной модуляции. Частота может меняться от нескольких единиц до сотен герц, что в миллиарды раз медленнее, чем самые быстродействующие переключательные электронные схемы.
Тем не менее сложные решения по восприятию информации, как, например, распознаванию лица, человек принимает за несколько сотен мс. Эти решения контролируются сетью нейронов, которые имеют скорость выполнения операций всего несколько мс. Это означает, что вычисления требуют не более 100 последовательных стадий. Другими словами, для таких сложных задач мозг «запускает» параллельные программы, содержащие около 100 шагов. Это известно как правило ста шагов. Количество информации, посылаемое от одного нейрона другому, тоже очень мало – несколько бит. Отсюда следует, что основная информация не передается непосредственно, а захватывается и распределяется в связях между нейронами. Этим объясняется такое название, как коннекционистская модель (connection – связь), применяемое к модели описывающей способ хранения информации в биологических нейронных сетях.
Искусственная нейронная сеть
В основу концепции искусственной нейронной сети положена вышеупомянутая коннекционистская модель, или, говоря более широко, принцип коннекционизма. Коротко этот принцип можно выразить так: «структура связей все, свойство элементов ничто». В более развернутом виде с коннекционизмом связан следующий блок идей:
- Однородность системы. Элементы одинаковы и чрезвычайно просты. Все определяется структурой связей между элементами.
- Надежная система из ненадежных элементов.
- «Голографичность» системы. При разрушении случайно выбранной части система сохраняет свои свойства.
Предполагается, что широкие возможности систем связей компенсируют бедность выбора элементов, их ненадежность и возможные разрушения части связей. Искусственную нейронную сеть можно рассматривать как направленный граф со взвешенными связями, в котором узлами являются некоторые элементарные процессоры, называемые искусственными нейронами. Устройство этих процессоров согласно коннекционистскому подходу должно быть достаточно простым и обычно выбирается следующим (рис. 2).
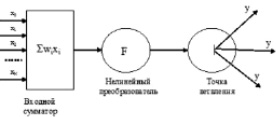
Рис. 2. Математический нейрон
- Нейрон имеет определенное число входных каналов, по которым он от своих «корреспондентов» – других нейронов или входных узлов нейронной сети получает «сигналы».
- Каждый «сигнал» ‒ это некоторое действительное число. Получив набор сигналов по своим входным каналам, нейрон умножает каждый сигнал на весовой коэффициент, соответствующий данному входу и суммирует полученные произведения. Набор этих весовых коэффициентов называется весовым вектором нейрона и является настраиваемой характеристикой нейрона.
- Результат суммирования подвергается нелинейному преобразованию посредством так называемой функции активации нейрона.
- Полученный результат является выходным сигналом нейрона, который рассылается всем «адресатам» данного нейрона. Это могут быть другие нейроны или выходные узлы нейронной сети.
Здесь наблюдается определенная аналогия с биологическим нейроном: входные и выходной каналы имитируют дендриты и аксоны, веса связей соответствуют синапсам, а функция активации отражает активность сомы.
В математическом контексте можно сказать, что нейрон осуществляет отображение Rn → R в соответствии с соотношением для его выхода:
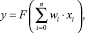
где x1, …, xn – входы нейрона; w1,…, wn – весовые коэффициенты синаптических связей нейрона. При этом x0 = –1, а w0 – пороговый уровень нейрона. F(x) – «функция активации» нелинейный преобразователь сигнала. В качестве такого нелинейного преобразователя в искусственных нейронных сетях обычно используются сигмоидные функции:
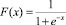 ,
,
функции гиперболического тангенса:
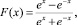
а также бинарные функции различного определения.
Главное в нейронной сети ‒ это архитектура связей и весовые коэффициенты, соответствующие этим связям. Архитектура связей это то, каким образом из отдельных нейронов сформирована сеть. Строго говоря, ее можно формировать как угодно, лишь бы входы нейронов получали какие-нибудь сигналы. Однако обычно используется несколько стандартных архитектур. Точнее, мы остановимся на двух классах архитектур:
а) сети прямого распространения, в которых графы не имеют петель;
б) рекуррентные сети, или сети с обратными связями.
Среди сетей первого класса наиболее распространены так называемые многослойные персептроны (рис. 3).
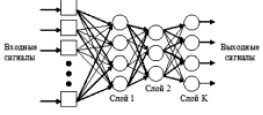
Рис. 3
В этих сетях нейроны расположены в несколько слоев. Нейроны первого слоя получают входные сигналы, преобразуют их и передают нейронам второго слоя. Далее сигнал обрабатывает второй слой и т.д. до слоя K, который выдает выходные сигналы для интерпретатора или пользователя. Обычно каждый выходной сигнал слоя i подается на вход всех нейронов слоя i + 1. Число нейронов в каждом слое может быть любым и никак заранее не связано с количеством нейронов в других слоях. Особенно широко распространены трехслойные сети, в которых каждый слой имеет свое наименование: первый входной, второй скрытый, третий выходной.
В работе [2] подобный подход успешно использован для вычисления коэффициента максимальной подъемной силы профилей крала летательного аппарата. (Параметры выборки профилей: разброс по толщинам от 5 до 34 %, максимальный прогиб 9.7 % [7]). На основе расчетных данных было проведено обучение и тестирование нейронных сетей по определению коэффициента максимальной подъемной силы профиля и положения точки отрыва, при котором он достигается. В качестве входного вектора для нейронной сети использовалась таблица ординат профиля. Следует отметить, что результаты расчета по этой программе хорошо согласуются с экспериментальными данными, и она широко используется при проектировании высоконесущих профилей.
В данной работе предлагается подобный подход для эффективного определения АДХ воздушно-космических систем. В качестве входных сигналов x1, …, xn (рис. 2, 3) проведен параметрический расчет аэродинамических характеристик для простых тел (пластина, сфера, конус), а также реальных компоновок воздушно космических систем («Буран», «Клипер», «Space Shuttle», «Falcon- HTV-2») (рис. 4) [9, 10].
Исходные данные. Гиперзвуковое обтекание, широкий диапазон чисел Рейнольдса Re (высота полета H изменяется от нуля до 10 000 км), при столкновении молекул газа с поверхностью рассматриваются различные потенциалы взаимодействия (комбинация зеркального и максвелловского отражения, модель Черчиньяни‒Лампис-Лорда (CLL), модель Леннарда‒Джонса) [10], диапазоны углов атаки a, скольжения b и крена g от -90° до +90° и различных температурных факторах tw = Tw/T0.
Здесь Tw – температура поверхности тела, а T0 – температура торможения потока.
«Клипер» «Falcon-HTV-2»


Рис. 4
Для вычисления АДХ обтекаемых тел использовалась разработанная в МФТИ и ЦАГИ и хорошо зарекомендовавшая себя для подобных задач информационная технология АДАНАТ (Аэродинамический анализ в обеспечении создания аэрокосмической техники). В качестве элементов АДАНАТ включает в себя методику решения кинетических уравнений методами статистического моделирования (Монте-Карло), решение уравнений сплошной среды (АРГОЛА-2), когнитивные методы [3].
На результатах расчета проводится обучение предложенной нейронной сети.
Методы Монте-Карло. Методы прямого статистического моделирования [9] в динамике разреженных газов, безусловно, занимают центральное место. К настоящему времени безусловный приоритет в динамике разреженного газа принадлежит методу Бёрда, модификации которого трудами отечественных исследователей О.М. Белоцерковского, В.Е. Яницкого, М.С. Иванова, В.А. Перепухова, А.И. Ерофеева, Ю.И. Хлопкова позволили буквально на порядки повысить эффективность метода. Суть метода заключается в том, что эволюция системы на малом промежутке времени Δt → 0 расщепляется на два ясных физических процесса:
1) релаксацию в соответствии с оператором столкновений в кинетическом уравнении
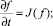
2) свободномолекулярный перенос
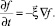
Это хорошо известная схема расщепления первого порядка по Δt для любого операторного уравнения, но в данном случае она подкупает тем, что расщепляет динамику такой сложной кинетической системы на два ясных физических процесса. Функция распределения моделируется N частицами, которые на первом этапе в каждой ячейке между собой сталкиваются в соответствии с частотой столкновения на протяжении времени Δt, а на втором, в течение Δt, перелетают на расстояния 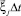 .
.
Когнитивный метод. Для сокращения времени проектирования и числа дорогостоящих натурных, и стендовых экспериментов, а также трудоемких много ресурсных расчетов создаются специализированные компьютерные системы типа Knowledge Based Engineering. Когнитивные технологии в информатике – это совокупность методов, алгоритмов и программ, моделирующих познавательные способности человеческого мозга для решения конкретных прикладных задач. Это задачи – распознавания образов (речи, сигналов, изображений, сцен и т.д.), выявления и идентификации закономерностей в массивах данных, решения задач компьютерного проектирования сложных систем, систем поддержки принятия решений в условиях нечетких входных данных и взаимосвязей и т.д. В последние годы стали развиваться физико-математические модели, основанные именно на когнитивном подходе. Такие модели строятся на основе научного и интуитивного анализа базы данных, полученной путем теоретического, экспериментального (летного, трубного, стендового), численного исследований, проведенных с различными объектами рассматриваемого класса. Построенные таким образом модели фактически имитируют как источники получения данных, основанные на некоторой исходной модели, так и сами модели, созданные на основе изучения физики процессов [10].
В качестве примера приведены некоторые расчетные данные для Клипера и Falcon.
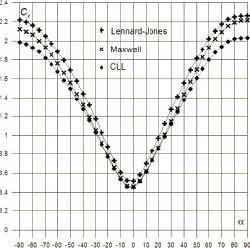
Рис. 5. Обтекание «Клипера». Зависимости Cx(α) от различных потенциалов взаимодействия молекул с поверхностью
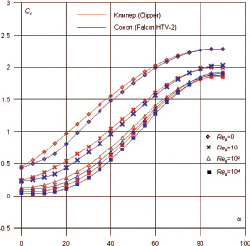
Рис. 6. Зависимость Cx(a) от числа Re для «Клипера» и «Falcon HTV-2» (tw = 0,1)
На подобной системе можно решать множество оптимизационных задач. В частности, определение параметров, обеспечивающих min сопротивления или max качества на ответственных участках траектории, выбор оптимальной траектории для необходимого посадочного маневра и др.
Заключение
По результатам проведения данной научно-исследовательской работы показана перспективность применения систем с элементами искусственного интеллекта в интересах аэрокосмической отрасли. Применение нейронных сетей на этапе проектирования ЛА позволяет существенно повысить достоверность оценки характеристик устойчивости и управляемости ЛА, что делает возможным сократить затраты на создание систем за счет уменьшения затрат на натурные испытания и трудоемкие вычисления.
Работа выполнена при поддержке РФФИ (Грант № 14-07-00564-а).
Рецензенты:
Боголепов В.В., д.ф.-м.н., главный научный сотрудник ФГУП «ЦАГИ», профессор МФТИ, г. Жуковский;
Липатов И.И., д.ф.-м.н., профессор, начальник отдела ФГУП «ЦАГИ», г. Жуковский.
Работа поступила в редакцию 17.01.2014.
Библиографическая ссылка
Хлопков Ю.И., Хлопков Ю.И., Дорофеев Е.А., Зея Мьо Мьинт, Поляков М.С., Хлопков А.Ю., Агаева Илаха Рустам Кызы РАЗРАБОТКА НЕЙРОННЫХ СЕТЕЙ ДЛЯ РАСЧЕТА АЭРОДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ВЫСОКОСКОРОСТНЫХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ // Фундаментальные исследования. 2013. № 11-9. С. 1834-1840;URL: https://fundamental-research.ru/ru/article/view?id=33466 (дата обращения: 06.03.2026).



