Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Бильгаева Л.П. 1 Самбялов З.Г. 1

---

1 ФГБОУ ВПО «Восточно-Сибирский университет технологий и управления»

Разработан алгоритм кластеризации категориальных данных с неполным обучением. Предложенный алгоритм основан на модификации алгоритма кластеризации CLOPE. Проведена оценка качества алгоритмов кластеризации и их сравнительный анализ на основе вычисления индексов качества кластеризации. В комплексной оценке алгоритмов кластеризации кроме стандартных индексов использовался предложенный нами индекс оптимального соответствия. Данный индекс определяет долю корректно определённых кластеров. В процессе сравнительного анализа предложенного индекса со стандартными индексами качества выявлено, что индекс оптимального соответствия предпочтительнее применять в том случае, когда в эталонном разбиении имеются кластеры малых размеров, при этом оценивается корректность определения этих кластеров. Результаты комплексной оценки предлагаемого способа кластеризации, выполненной на основе проведенного тестирования, показывают, что модифицированный алгоритм кластеризации имеет более высокие показатели индекса качества по сравнению со стандартным алгоритмом CLOPE.

Статья в формате PDF

420 KB

интеллектуальный анализ данных

кластеризация с неполным обучением

оценка качества кластеризации

категориальные данные

1. Бильгаева Л.П., Самбялов З.Г. Модификация алгоритма кластеризации CLOPE // Фундаментальная наука и технологии – перспективные разработки: сб. ст. II междунар. науч.-практ. конф. Т.2. – М.: Изд-во НИЦ «Академический», 2013. – С. 86–90.

2. Бильгаева Л.П., Самбялов З.Г. Один способ оценки качества кластеризации //Развитие информационных технологий и их значение для модернизации социально-экономической системы: сб. ст. III междунар. науч.-практ. конф. – Саратов: Изд-во ЦПМ «Академия Бизнеса», 2013. – С. 18–23.

3. Кулаичев А.П. Методы и средства комплексного анализа данных. – М.: ИНФРА-М, 2006. – 512 c.

4. Паклин Н.Б. Кластеризация категорийных данных: масштабируемый алгоритм СLOPE [Электронный ресурс] // Научная библиотека BaseGroup Labs. URL: http://www.basegroup.ru/library/analysis/clusterization/clope.

5. Nizar Grira, Michel Crucianu, Nozha Boujemaa. Unsupervised and Semi-supervised Clustering: a Brief Survey. In Proc. Of 7th ACM SIGMM international workshop on Multimedia information retrieval, 2004.

6. Yang, Y., Guan, H., You. J. CLOPE: A fast and Effective Clustering Algorithm for Transactional Data In Proc. of SIGKDD’02, 2002.

Классический подход к задаче кластеризации предполагает полностью автоматический процесс без возможности задания каких-либо априорных данных/правил при решении задачи. Это приводит к тому, что повлиять на результат кластеризации никак нельзя, итоговый результат во многом зависит от выбранного алгоритма кластеризации. Однако часто возникают ситуации, когда имеется небольшое количество априорных данных, которое можно (или даже необходимо) использовать при кластеризации. В целом подход использования априорных знаний в процессе решения задачи кластеризации получил название кластеризации с неполным обучением [5].

Использование априорных данных позволяет повысить качество кластеризации. Априорное знание может быть как известным ранее фактом, так и выдвигаемой аналитиком гипотезой. Неполное обучение делает процесс кластеризации гибким и управляемым посредством задания различных гипотез. Таким образом, аналитик получает возможность произвести кластеризацию согласно определённым правилам, которые продиктованы целью его исследования.

Реализация подхода неполного обучения в настоящее время реализуется посредством модификации существующих алгоритмов кластеризации без учителя. Большинство работ, развивающих тему кластеризации с неполным обучением, посвящено модификации алгоритма К-средних. Поскольку алгоритм K-средних используется для кластеризации данных числового типа, то существует необходимость разработки кластеризации с неполным обучением данных категориального типа. В настоящее время предложено достаточно много методов для работы с категориальными данными. Одним из эффективных считается алгоритм CLOPE [4]. В данной работе предлагается алгоритм кластеризации с неполным обучением, в основе которого лежит алгоритм CLOPE [6]. Также предложен способ оценки данного алгоритма на основе индекса оптимального соответствия.

1. Модифицированный алгоритм кластеризации CLOPE с неполным обучением

В рамках кластеризации с неполным обучением имеется некоторое априорное знание об анализируемых данных, например, априорные сведения о значимости некоторых атрибутов в формировании кластеров. Значимость атрибута выражается числовой величиной, называемой весовым коэффициентом атрибута. Каждому атрибуту ai ставится в соответствие действительное положительное число wi – весовой коэффициент. Чем больше значение весового коэффициента, тем больше вклад атрибута в формирование кластеров. В стандартном алгоритме CLOPE весовые коэффициенты всех атрибутов равны единице, т.е. атрибуты равнозначны при формировании кластеров. Изменив исходные значения весовых коэффициентов, можно получить в конечном итоге существенно отличающийся состав кластеров [1].

В отличие от стандартного CLOPE, в модифицированном алгоритме предлагается вычислять следующие дополнительные характеристики кластера:

1) ai – номер атрибута, которому принадлежит значение i;

2) А(C) – множество уникальных значений атрибутов в кластере С.

Кроме того, предлагается изменить способ вычисления следующих характеристик кластера:

1) 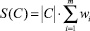– площадь кластера;

2) 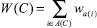– ширина кластера.

Рассмотрим пример, иллюстрирующий суть предлагаемой модификации. В качестве исходных данных используем данные о вулканах, представленные в таблице.

Исходные данные

Кластеризация стандартным алгоритмом CLOPE позволяет получить следующее разбиение {{Везувий}, {Килиманджаро}, {Ключевская Сопка}, {Таупо}, {Казбек}, {Катман, Сент-Хеленс}, {Кракатау, Эйяфьядлайёкюдль}} при коэффициенте отталкивания, равном 2,6. Разбиение содержит 5 кластеров с одним объектом и 2 кластера с двумя объектами. Из таблицы видно, что в два последних кластера вошли вулканы с абсолютно совпадающими значениями атрибутов (исключение составляет последний кластер, где имеется различие в значении атрибута «Местоположение»).

Выполним кластеризацию с приоритетом по типу местоположения. При этом атрибуту «Тип местоположения» задается весовой коэффициент 2. В результате работы алгоритма получается следующее разбиение {{Килиманджаро}, {Таупо}, {Казбек}, {Везувий, Катман, Сент-Хеленс, Ключевская Сопка}, {Кракатау, Эйяфьядлайёкюдль}}. На рис. 1 представлена гистограмма самого большого кластера в разбиении {Везувий, Катман, Сент-Хеленс, Ключевская Сопка}.

Из гистограммы видно, что кластер состоит из действующих вулканов, извергавшихся во втором тысячелетии и расположенных на материке. Последний факт был учтен как основополагающий при формировании кластера. Если бы весовой коэффициент атрибута «Тип местоположения» равнялся единице, то высота кластера составила бы .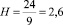

Такое значение высоты уже не обеспечивает максимальное значение глобальной функции оптимизации и, соответственно, такой кластер невозможно получить при использовании стандартного алгоритма CLOPE.

2. Оценка качества кластеризации

Оценка качества полученной структуры кластеров является одним из важных этапов в процессе кластеризации. Большинство методов оценки качества кластеризации используют количественные показатели, называемые индексами или метриками [2]. Наиболее используемыми являются следующие индексы качества кластеризации: индекс Рэнд, индекс Жаккара, индекс Фолкса-Маллоус и индекс чистоты кластеров.

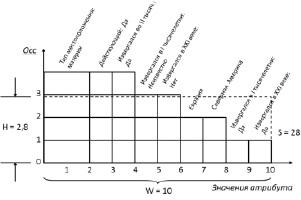
Рис. 1. Гистограмма кластера в модифицированном алгоритме CLOPE

Как правило, оценка качества производится на заранее подготовленных данных. Тестовые данные формируются по заранее подготовленной схеме, каждый объект исходного множества маркируется номером или названием исходного класса. Результат кластеризации сравнивается с эталонным разбиением и вычисляется индекс качества.

2.1. Оценка качества кластеризации на основе индекса оптимального соответствия

В данной работе для оценки качества кластеризации предлагается индекс оптимального соответствия. Вычисление данного индекса заключается в поиске такого инъективного отображения множества эталонных кластеров в множество кластеров итогового разбиения, при котором сумма пересечений эталонных кластеров и итоговых кластеров является максимальной. Рассмотрим процедуру вычисления индекса оптимального соответствия.

Пусть, A1, ..., Ak – эталонные кластеры, полученные в результате генерации исходного массива данных;

k – эталонное количество кластеров;

ni – количество объектов в i-м кластере;

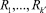– кластеры, полученные в ходе выполнения алгоритма;

k′ – количество кластеров, которое было определено алгоритмом кластеризации.

Для оценки качества кластеризации необходимо получить однозначное соответствие эталонного кластера Ai результирующему кластеру 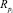. Множество индексов {p1, ..., pk} должно быть подобрано таким образом, чтобы максимизировать сумму ci – количества верно определенных объектов в эталонном кластере Ai. Исходя из этого, ci определяется по следующей формуле

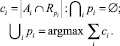(1)

Определив количество верно определенных объектов ci, вычисляем индекс оптимального соответствия по формуле:

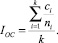(2)

В формуле (2) числитель представляет собой сумму степеней корректности определения кластеров. Определим область значений индекса качества кластеризации. Наименьшее значение индекса качества кластеризации возможно в том случае, если алгоритм определяет каждый объект в отдельный кластер. Тогда значение индекса равно:

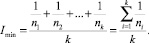(3)

Наибольшее значение индекса качества кластеризации возможно в том случае, если алгоритм точно определил количество кластеров, и корректно определил состав кластеров. Степень корректности определения каждого кластера равна единице. Значение индекса при этом также равно единице:

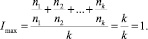(4)

Таким образом, область значений индекса качества кластеризации определена на отрезке 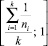, где k – априорное количество кластеров.

Особенностью данного метода оценки является то, что степень корректности определения кластеров имеет равный вклад в значение индекса вне зависимости от размера определяемых кластеров. Это может иметь эффект в том, случае если эталонное разбиение имеет большое количество малых по размеру кластеров.

Предложенный в данной работе способ оценки качества кластеризации предпочтительнее применять в том случае, когда в эталонном разбиении имеются кластеры малых размеров, и при этом необходимо оценить корректность определения этих кластеров [2]. В случае необходимости оценивания общей доли верно сопоставленных объектов эталонным кластерам следует использовать методы с индексами Rand, Jaccard или FM. При малом количестве эталонных кластеров применим метод с индексом «Чистота кластера». Таким образом, каждый индекс качества имеет собственную «точку зрения» о качестве кластеризации и в различных ситуациях имеет большую или меньшую применимость. В общем случае для более полной оценки качества кластеризации целесообразно использовать несколько различных методов оценки качества.

2.2. Оценка модифицированного алгоритма CLOPE по индексу оптимального соответствия

Для сравнительного анализа алгоритмов CLOPE и модифицированного CLOPE проведено тестирование алгоритмов на наборах данных из открытого репозитория UCI Machine Learning [3]. Репозиторий UCI Machine Learning является крупнейшим открытым хранилищем реальных и модельных задач интеллектуального анализа данных. Для тестирования выбран набор данных о зоопарке (Zoo dataset). Набор содержит 101 транзакцию со сведениями о животных. Каждая транзакция содержит 18 атрибутов с описанием характеристик животного: название животного, 15 различных логических атрибутов, 1 целочисленный атрибут количества конечностей животного и атрибут биологического класса животного.

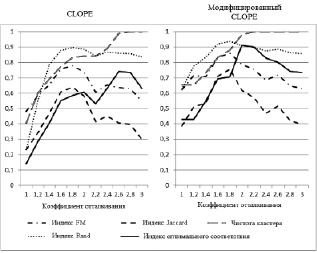
Рис. 2. Оценка результатов модифицированного алгоритма CLOPE

Была проведена серия тестов при различных значениях коэффициента отталкивания. Все результаты оценены индексами качества Rand, Jaccard, FM, оптимального соответствия и «Чистота кластера» по атрибуту «Биологический класс животного». Результаты тестирования представлены на рис. 2. При кластеризации модифицированным алгоритмом был установлен весовой коэффициент со значением 2 у атрибута «Биологический класс животного». Значение весового коэффициентов у данного атрибута было увеличено, поскольку значения данного атрибута являются наиболее значимыми при формировании кластеров. Все остальные атрибуты имеют весовой коэффициент,. равный единице.

Таким образом, результаты тестирования показывают, что модифицированный алгоритм CLOPE имеет более высокие значения индексов качества. При этом следует отметить увеличение значение индекса «Чистота кластера». Например, у атрибута «Биологический класс животного» был увеличен весовой коэффициент и по данному атрибуту определялся индекс чистоты. Из этого следует, что значение весового коэффициента атрибута прямо пропорционально значению индекса «Чистота кластера» по данному атрибуту.

Заключение

В предложенном в данной работе модифицированном алгоритме CLOPE используется неполное обучение, которое заключается в задании атрибутам весовых коэффициентов. Достоинством предложенного похода является то, что весовые коэффициенты позволяют управлять процессом кластеризации и получать структуру кластеров с различной чистотой значений по атрибутам.

Дополнительные временные затраты, возникающие в связи с модификацией алгоритма CLOPE, являются незначительными и заключаются в расчете величин a(i) и А(C). Однако благодаря модификации алгоритм CLOPE становится более гибким в настройке и позволяет решать задачу кластеризации с заданными условиями.

Рецензенты:

Мижидон А.Д., д.т.н., профессор, зав. кафедрой «Прикладная математика», Восточно-Сибирский государственный университет технологий и управления, г. Улан-Удэ;

Ширапов Д.Ш., д.ф-м.н, профессор, зав. кафедрой «Электронно-вычислительные системы», Восточно-Сибирский государственный университет технологий и управления, г. Улан-Удэ.

Работа поступила в редакцию 15.01.2014.

Библиографическая ссылка