Лечебно-профилактическое учреждение является динамической саморазвивающейся и адаптирующейся системой, входящей в качестве элемента в общую систему охраны здоровья граждан России, управление в которой построено по традиционному иерархическому принципу: министерство, региональные власти, муниципальные органы управления, главный врач, заведующий отделением (лабораторией). В данной системе предполагается относительно демократическое согласование основных решений, принимаемых управляющими органами разного уровня. Управление всеми видами деятельности лечебно-профилактических учреждений осуществляется в соответствии с законами об организации медицинской помощи в Российской Федерации, постановлениями, приказами и инструкциями Министерства здравоохранения РФ, региональных, муниципальных органов, приказами главного врача, распоряжениями заведующих отделениями и лабораториями.
Характерной особенностью деятельности лечебно-профилактических учреждений в целом является непрерывное воздействие множества детерминированных (определенных), стохастических (статистически определенных) и неопределенных факторов:
- Обращение в ЛПУ пациента за первичной медицинской помощью или госпитализация.
- Наблюдение пациента у врача первичного звена (врач общей практики, участковый терапевт, педиатр).
- Консультация пациента у узкого специалиста.
- Обследование пациента по различным направлениям
- Выписка пациента с различными результатами (выздоровление, улучшение, ухудшение и т.д.).
- Возможности диспансерного наблюдения и проведения профилактических осмотров.
- Наличие или отсутствие достаточного количества высококвалифицированных участковых врачей первичного звена (врач общей практики, участковый терапевт, педиатр).
- Наличие или отсутствие высококвалифицированных врачей узкой специализации (офтальмолог, невропатолог, эндокринолог и т.д.).
- Наличие развитой компьютерной интегрированной информационно – аналитической системы.
В качестве исходных положений, учитываемых в предлагаемой концептуальной модели управления качеством оказания медицинской помощи, принимаются следующие утверждения:
- Лечебно-профилактическое учреждение является сложной динамической системой, подверженной воздействию множества случайных, малоопределенных или неопределенных факторов.
- Управление системой оказания медицинской помощи осуществляется Министерством здравоохранения и социального развития РФ, департаментом здравоохранения, комитетом по здравоохранению, главным врачом, заведующими отделениями и лабораториями в основном по иерархическому принципу [1,2].
- Основной целью лечебно-профилакти-ческого учреждения является оказание высококвалифицированной медицинской помощи по обращению граждан, ведение диспансерного наблюдения и профилактических мероприятий в соответствии с требованиями государственных стандартов, потребностями региона и личности [3-5].
- Потребности определенной территории по охране здоровья граждан определяются структурой экономики, количеством и масштабами деятельности отраслевых предприятий, организаций и учреждений социальной сферы, количеством частных фирм и акционерных обществ, неработающего населения (детей, пенсионеров, безработных и т.д.). Потребности на ближайшую перспективу определяются экономическим состоянием региона, климато - географическими особенностями региона, воздействием экологических факторов, половозрастным составом населения с учетом стажа проживания на Севере и национальным составом с учетом миграционных процессов.
Математические модели управления оказанием медицинской помощи в ЛПУ должны учитывать все основные показатели.
Согласно доктрине «гибкого» управления, вышестоящие органы управления ЛПУ при ежегодной корректировке министерской методики расчета повышают значения показателей деятельности ЛПУ по новым и наиболее необходимым для социально-экономического и демографического развития России и понижают показатели деятельности по устаревающим направлениям для того, чтобы плавно изменить структуру и деятельность ЛПУ в желаемом направлении.
Математическая модель управления должна обеспечиваться информационной поддержкой на основе решения следующих задач:
- Статистический учет показателей состояния и результатов деятельности различных подразделений ЛПУ и лечебно-профилак-тического учреждения в целом.
- Анализ и прогноз динамических показателей материально-технической базы, научной и информационной базы ЛПУ.
- Оптимальное распределение общей нагрузки на врача в ЛПУ различного профиля.
- Оптимальное распределение нагрузки на врача с учетом диспансеризации и профилактических мероприятий.
- Оптимальное распределение использования общего фонда площадей и материально-технической базы.
- Управление процессами диспансеризации.
- Управление процессами профилактических осмотров.
- Управление профилактической и просветительской работой среди населения.
- Управление потребностью в специализированных видах медицинской помощи.
- Определения муниципальными и региональными властями приоритетов в развитии направлений деятельности по охране здоровья граждан на уровне муниципалитета, региона, страны.
В настоящее время в г. Сургуте (ХМАО - Югра)функционирует программный комплекс «Медицинская статистика муниципального здравоохранения», объединяющая информационное пространство всех ЛПУ, действующих на территории города, а также Единая информационная система обязательного медицинского страхования, имеющие достаточно большой статистический материал, который можно использовать как базу данных для информационной поддержки многих из указанных задач.
Изучению динамики процесса оказания медицинской помощи посвящено достаточно большое количество работ, отражающих те или иные аспекты этого сложного социально–психологического вида человеческой деятельности. При этом вопрос рассматривается с социальной, физиологической, медицинской и психологической точек зрения. Поэтому каждый вид исследования сопровождается созданием тех или иных формальных математических моделей, основанных на определенных допущениях, отражающих специфику данного исследования. В данном случае нас будет интересовать один из видов процесса оказания медицинской помощи -– профилактический осмотр населения.
Профилактические осмотры работающих в разных областях экономики – это национальный проект «Здоровье», которым начинается новый важный этап развития здравоохранения. Углубленное обследование здоровья в 2006 году пройдут 4 млн. россиян, в 2008 – еще 8 млн. Авторы реформы считают, что профилактические осмотры станут реальным шагом на пути поворота нашего здравоохранения от «лечения болезней» к «сохранению здоровья».
Рассмотрим процесс профилактического осмотра как массового вероятностного явления, основой моделирования которого служит теория случайных процессов. При этом процесс профосмотра можно представить в виде последовательности случайных событий, переводящих объект из одного состояния в другое. Для описания таких процессов, в которых изучаемый объект дискретно изменяет свое состояние под действием случайных событий, успешно применяются математические модели, основанные на применении аппарата дискретных Марковских цепей [1].
Введем следующие допущения:
- процесс перехода от одного этапа профосмотра к другому происходит скачкообразно;
- вероятность перехода в каждое последующее состояние зависит только от предыдущего состояния (отсутствие последействия).
Эти допущения и позволяют интерпретировать процесс профосмотра как дискретную Марковскую цепь.
В процессе профосмотра пациента могут произойти следующие события:
А1 - пациент получает информацию о необходимости пройти обследование;
А2 – у пациента возникает желание (возможность) пройти обследование.
В результате пациент может оказаться в одном из следующих состояний:
![]() - соответственно готовность или неготовность к прохождению профилактического осмотра;
- соответственно готовность или неготовность к прохождению профилактического осмотра;
![]() - соответственно желание или нежелание подвергаться медицинскому осмотру.
- соответственно желание или нежелание подвергаться медицинскому осмотру.
Так как процесс профосмотра происходит в единой взаимосвязанной системе, преследующей единую цель – готовность и желание человека подвергнуться медицинскому осмотру, то целесообразно будет объединение (укрупнение) состояний в следующий набор, образующий вектор состояний:
![]() (1)
(1)
где ![]() – пациент знает о необходимости пройти обследование и желает пройти обследование;
– пациент знает о необходимости пройти обследование и желает пройти обследование; ![]() – пациент знает, но не желает пройти обследование;
– пациент знает, но не желает пройти обследование; ![]() – пациент не имеет информации, но хотел бы пройти обследование;
– пациент не имеет информации, но хотел бы пройти обследование;![]() – не знает и не желает подвергаться профилактическому осмотру:
– не знает и не желает подвергаться профилактическому осмотру:
Дискретная Марковская цепь (ДМЦ) считается заданной, если известна переходная матрица и вектор начальных вероятностей, характеризующей начальное состояние системы. Поскольку целью процесса подготовки населения к сбережению своего здоровья является состояние ![]() , то, очевидно, оно будет поглощающим. Соответственно, поглощающей будет и ДМЦ. Кроме того, при анализе состояний будем полагать, что некоторые переходы
, то, очевидно, оно будет поглощающим. Соответственно, поглощающей будет и ДМЦ. Кроме того, при анализе состояний будем полагать, что некоторые переходы ![]() , а также
, а также ![]() и
и ![]() будут невозможными, и соответствующие переходные вероятности будут равны нулю:
будут невозможными, и соответствующие переходные вероятности будут равны нулю: ![]() . Примем также, что поскольку исходным состоянием считается
. Примем также, что поскольку исходным состоянием считается ![]() , то вектор начальных вероятностей имеет вид:
, то вектор начальных вероятностей имеет вид:
![]() (2)
(2)
С учетом сделанных замечаний переходная матрица, описывающая поведение системы на одном шаге процесса, будет иметь вид:
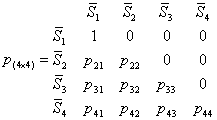 (3)
(3)
данный процесс можно также наглядно представить в виде взвешенного графа (рис.1):
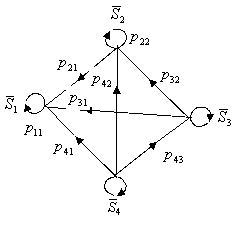
Рис.1. Взвешенный граф дискретной Марковской цепи, представляющей процесс профилактической работы среди населения
Для дальнейшего получения функции, описывающей эффективность мероприятий по проведению просветительской работы среди населения, необходимо оценить возможные варианты изменения состояний на пути от исходного до поглощающего состояния. В теории ДМЦ [3] эти варианты подсчитываются с помощью фундаментальной матрицы вида:
![]() , (4)
, (4)
где ![]() - единичная матрица;
- единичная матрица; ![]() - подматрица, описывающая внутренние переходы в невозвратное множество состояний; (-1) – знак обращения матрицы: (
- подматрица, описывающая внутренние переходы в невозвратное множество состояний; (-1) – знак обращения матрицы: (![]() ).
).
После соответствующих преобразований матрица (4) будет иметь следующий вид:
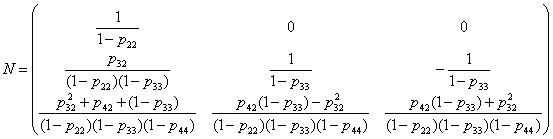 (5)
(5)
Элементы матрицы (5) означают среднее число попаданий объекта в то или иное состояние до перехода в поглощающее состояние. Однако, более интересным будет суммарное число попаданий в то или иное состояние до перехода в поглощающее. Это число подсчитывается по формуле:
![]() , (6)
, (6)
где ![]() - вектор – столбец, состоящий из единиц.
- вектор – столбец, состоящий из единиц.
В нашем случае вектор-столбец суммарных средних имеет вид:
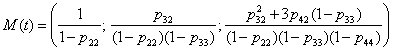 (7)
(7)
Так как ![]() , то очевидно, что наиболее быстрое продвижение к поглощающему состоянию будет из состояния
, то очевидно, что наиболее быстрое продвижение к поглощающему состоянию будет из состояния ![]() . Это легко объясняется физически. При выводе формул (6) и (7) мы предполагали, что процесс начинается с исходного состояния
. Это легко объясняется физически. При выводе формул (6) и (7) мы предполагали, что процесс начинается с исходного состояния ![]() и вектор начальных вероятностей имеет вид (2). Однако в действительности вероятности других начальных состояний могут не равняться нулю (например, пациент знает о необходимости время от времени проходить медицинское обследование или же он имеет некоторые проблемы со здоровьем и т.п.). Тогда вектор вероятностей может иметь более близкий к реальности вид, например:
и вектор начальных вероятностей имеет вид (2). Однако в действительности вероятности других начальных состояний могут не равняться нулю (например, пациент знает о необходимости время от времени проходить медицинское обследование или же он имеет некоторые проблемы со здоровьем и т.п.). Тогда вектор вероятностей может иметь более близкий к реальности вид, например:
![]() (8)
(8)
причем обязательными условиями являются:
![]() и
и ![]()
В этом случае теория дискретных Марковских цепей дает следующие решения:
![]() (9)
(9)
Для получения целевой функции, учитывающей затраты на подготовительную работу к проведению профилактических осмотров и ее эффективность, следует связать затраты на пребывание пациента в том или ином состоянии и на последующие переходы из одного состояния в другое. Допустим, что в подготовительный период используются следующие формы работы:
- сбора информации о текущей ситуации по оснащенности поликлинических учреждений необходимой аппаратурой и обеспеченностью квалифицированными медицинскими кадрами и т.п.
- проведение научных исследований на основе данных о состоянии здоровья граждан в регионе, половозрастном составе и т.п.;
- проведение научных исследований на основе предыдущего профилактического осмотра;
- разработке соответствующих графиков проведения профилактических осмотров;
- беседы медицинских работников на предприятиях;
- изготовление и распространение рекламных материалов;
Все эти формы связаны, во-первых, с определенными затратами и, во-вторых, влияют на вероятности и время пребывания пациента в том или ином состоянии. Эти зависимости должны быть получены экспертным путем.
В совокупности набор величин затрат, соответствующий набору состояний пациента, образует вектор управления:
![]() (10)
(10)
Таблица 1 отражает связь выражения (10) с вероятностями перехода и состояниями.
Таблица 1. Связь затрат на подготовку к профилактическому осмотру с состояниями пациента
| Состояние | | | |
| Расходы | | | |
Данная таблица должна уточняться путем соответствующих исследований. Таким образом, вектор-строка расходов, связанных с тем или иным состоянием, будет иметь вид:
![]() (11)
(11)
Для получения числовой функции в законченном виде необходимо умножить слева вектор-строку (11) на вектор-столбец (9), то есть:
![]() (12)
(12)
Подставив соответствующие выражения, получим выражение для целевой функции:
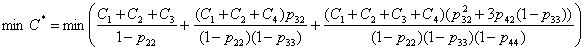 (13)
(13)
Полученное выражение (13) позволяет решить три задачи:
- Определить – соответствуют ли расходы на подготовительную работу к профилактическому осмотру населения располагаемыми средствами.
- Произвести поиск оптимальных значений
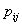 , обеспечивающих минимум
, обеспечивающих минимум 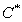 .
. - Оценить степень влияния каждой вероятности
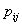 на общую эффективность мероприятия и наметить пути ее повышения.
на общую эффективность мероприятия и наметить пути ее повышения.
Данный вариант решения задачи представляет собой статический метод принятия оптимальных решений с помощью дискретной Марковской цепи. Преимущества этого метода – простота и наглядность, недостаток – статичность, т.е. невозможность адаптивного (оперативного) управления.
Математическая модель оценки эффективности профилактических осмотров на основе дискретных марковских цепей позволяет определить целевую функцию, учитывающую экономические затраты на основные виды подготовительной работы к проведению профилактических осмотров. Предлагаемая целевая функция на основе дискретных марковских цепей позволяет решить ряд важных задач, связанных с оптимальным распределением имеющихся ресурсов на проведение профилактических осмотров.
Реализация математических моделей на основе дискретных марковских цепей требует использования конкретных значений экономических показателей, оценивающих трудозатраты на проведение профилактических осмотров.
СПИСОК ЛИТЕРАТУРЫ:
- Вентцель Е.С., Теория случайных процессов и ее инженерные приложения: Учеб. пособие для студ. втузов /Е.С. Вентцель, Л.А. Овчаров. – 3-е изд., перераб. и доп. – М.: Издательский центр «Академия», 2003. – 432 с.
Работа представлена на IV научную международную конференцию «Инновационные технологии», 18-28 января 2007 г. Паттайа (Тайланд). Поступила в редакцию 12.02.2007 г.
Библиографическая ссылка
Алмазова Е.Г., Микшина В.С. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОЦЕНКИ ЭФФЕКТИВНОСТИ ПРОФИЛАКТИЧЕСКИХ ОСМОТРОВ НАСЕЛЕНИЯ // Фундаментальные исследования. 2007. № 7. С. 79-83;URL: https://fundamental-research.ru/ru/article/view?id=3333 (дата обращения: 04.02.2026).



