В основу всех способов астрометрии положен геометрический способ определения дистанции до космического объекта, когда наблюдение за ним ведется из двух пунктов наблюдения, расстояние между которыми известно, и с одновременным измерением углового перемещения объекта. Это позволяет из геометрических соотношений узнавать расстояние [1–5].
Этот ставший за много веков фундаментальным метод указывает на то, что используя только геометрические способы решения задачи определить дистанцию до объекта из одной точки наблюдения невозможно.
Эту мысль подтверждают и уравнения моделей слежения за объектом, которые для горизонтальной и вертикальной плоскости имеют следующий вид.
Модель изменения пеленга во времени:
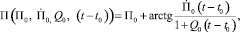 (1)
(1)
где П0 – пеленг цели в начальный момент времени; 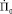 – временное изменение пеленга в начальный момент времени;
– временное изменение пеленга в начальный момент времени; 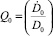 – относительное временное изменение дистанции в начальный момент времени;
– относительное временное изменение дистанции в начальный момент времени; 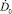 – временное изменение дистанции в начальный момент времени; D0 – дистанция до объекта в начальный момент времени; t – текущий момент времени; t0 – начальный момент времени, в дальнейшем (t – t0) обозначается через t.
– временное изменение дистанции в начальный момент времени; D0 – дистанция до объекта в начальный момент времени; t – текущий момент времени; t0 – начальный момент времени, в дальнейшем (t – t0) обозначается через t.
Модель изменения угла места объекта во времени:
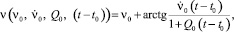 (2)
(2)
где ν0 – угол места в начальный момент времени; 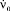 – временное изменение угла места в начальный момент времени.
– временное изменение угла места в начальный момент времени.
Этот опробованный геометрический метод был перенесён и на радиометрические наблюдения после изобретения радиотелескопов, которые значительно увеличили расстояние и точность наблюдения за космическими объектами по сравнению с оптическими методами.
В данной работе авторы предлагают метод пассивного определения расстояния до космических объектов с помощью одиночного радиотелескопа за счёт расширения информационного пространства измерений при условии равномерного и прямолинейного движения объекта и наблюдателя.
В самом деле, независимо от природы электромагнитного излучения космических объектов (синхротронные излучения, возникающие при движении релятивистских электронов в мощных магнитных полях, окружающих сверхмассивные черные дыры в галактических ядрах, квазары, свечение галактик как в радиодиапазоне, так и в инфракрасной области, видимом свете, ультрафиолете и так далее), мощность сигнала от объектов на входе антенны радиотелескопа обратно пропорциональна квадрату расстояния до источника излучения и убывает под воздействием среды по экспоненциальному закону.
Тогда, обозначив уровень сигнала в текущий момент времени через U(t),
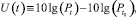 (3)
(3)
где Pt – мощность принятого сигнала в текущий момент времени; 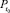 – мощность принятого сигнала в начальный момент времени; получим:
– мощность принятого сигнала в начальный момент времени; получим:
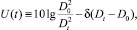 (4)
(4)
где δ – коэффициент километрического ослабления сигнала на трассе объект-наблюдатель; Dt – дистанция до объекта в текущий момент времени.
При равномерном и прямолинейном движении объекта и наблюдателя модель изменения во времени центрированного уровня сигнала имеет вид:
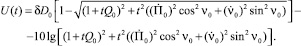 (5)
(5)
Анализ уравнений измерения (1–5) даёт возможность определить шестимерный вектор состояния
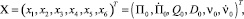 (6)
(6)
где X – вектор состояний; x1–x6 – компоненты вектора состояний.
Уравнение состояния в таком случае имеет вид
Xi+1 = Xi, (7)
где Xi+1 – вектор состояний в момент времени ti+1; Xi – вектор состояний в момент времени ti.
Так как уравнения измерения (1), (2), (5) являются нелинейными относительно составляющих вектора состояния, то необходимо линеаризовать эти уравнения в окрестности некоторой априорной оценки вектора состояния.
Чем точнее будет эта априорная оценка вектора состояния, тем быстрее будет сходимость дальнейших оценок (в процессе фильтрации по Калману) к истинному значению вектора состояния.
Уравнение калмановской фильтрации (вектор состояния шестимерный, вектор измерения трёхмерный) имеет вид
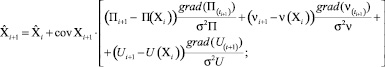 (8)
(8)
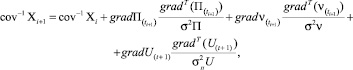 (9)
(9)
где 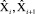 – оценки вектора состояния на i-й и (i + 1)-й моменты времени соответственно;
– оценки вектора состояния на i-й и (i + 1)-й моменты времени соответственно; 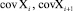 – оценки ковариационной матрицы вектора состояния на i-й и (i + 1)-й моменты времени соответственно;
– оценки ковариационной матрицы вектора состояния на i-й и (i + 1)-й моменты времени соответственно; 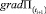 – градиент функции
– градиент функции 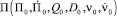 в (i + 1)-й момент времени;
в (i + 1)-й момент времени; 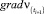 – градиент функции
– градиент функции 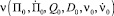 в (i + 1)-й момент времени; σ – среднеквадратичное отклонение;
в (i + 1)-й момент времени; σ – среднеквадратичное отклонение; 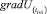 – градиент функции
– градиент функции 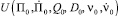 в (i + 1)-й момент времени;
в (i + 1)-й момент времени; 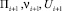 – измерения пеленга, угла места, центрированного уровня сигнала в тракте измерения пеленга, центрированного уровня сигнала в тракте измерения угла места соответственно;
– измерения пеленга, угла места, центрированного уровня сигнала в тракте измерения пеленга, центрированного уровня сигнала в тракте измерения угла места соответственно; 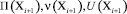 – прогнозы пеленга, угла места, центрированного уровня соответственно,
– прогнозы пеленга, угла места, центрированного уровня соответственно,
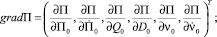 (10)
(10)
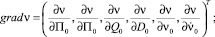 (11)
(11)
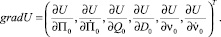 (12)
(12)
C помощью фильтра Калмана определяем компоненты вектора состояния, которые затем пересчитываем на заданный момент времени и по известным формулам определяем значения не только сферических координат (пеленг на объект (П), угол места (ν), дистанцию до объекта (D)), но и значение скорости и курса движения объекта.
Преимущества предлагаемого пассивного однопозиционного метода определения дистанции состоят в следующем:
- любой радиотелескоп может решать задачу определения дистанции до объекта независимо от других радиотелескопов;
- отпадает необходимость решения сложнейшей задачи по синхронизации измерений на базовых радиотелескопах;
- метод позволит повысить эффективность работы радиотелескопов, установленных на искусственных спутниках и звездолётах.
Метод признан изобретением и защищен патентами.
Рецензенты:
Галушкин А.И., д.т.н., профессор, начальник лаборатории, ФГАНУ «Центр информационных технологий и систем органов исполнительной власти», г. Москва;
Ипатов О.С., д.т.н., профессор, зав. кафедрой Балтийского государственного университета «Военмех им. Д.Ф. Устинова», г. Санкт-Петербург.
Работа поступила в редакцию 01.10.2013.
Библиографическая ссылка
Рудинский А.В., Шенгелия М.В. О ВОЗМОЖНОСТИ ОДНОПОЗИЦИОННОГО ОПРЕДЕЛЕНИЯ ДИСТАНЦИИ ДО ОБЪЕКТА В ПАССИВНОМ РЕЖИМЕ РАБОТЫ РАДИОТЕЛЕСКОПА // Фундаментальные исследования. 2013. № 11-4. С. 648-650;URL: https://fundamental-research.ru/ru/article/view?id=33176 (дата обращения: 12.03.2026).



