Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Сапогин В.Г. 1 Прокопенко Н.Н. 2 Манжула В.Г. 3 Сапунцов Н.Е. 1 Нестюрина Е.Е. 1

---

1 Таганрогский технологический институт Южного федерального университета

2 Институт сферы обслуживания и предпринимательства (филиал) Донского государственного технического университета

3 Негосударственное образовательное учреждение высшего профессионального образования «Институт коммуникативных технологий»

Предложен аналитический метод расчёта индуктивности сплошного немагнитного проводящего цилиндра произвольных геометрических размеров с азимутальной плотностью вихревого тока при наличии омических потерь и диамагнитных свойств токов Фуко. Получены радиальные распределения азимутальной компоненты вектора напряженности вихревого электрического поля, плотности токов Фуко, удельной тепловой мощности, выделяемой в локальной области проводящего цилиндра. Из энергетических соображений получена формула для вносимой индуктивности сплошного цилиндра. Показано, что индуктивность проводящего цилиндра обращается в нуль для двух характеристических частот системы и имеет положительные и отрицательные значения. Оценки, проведённые для латуни и плёнки из электронного кремния, указывают на то, что больших положительных значений индуктивности можно добиться в области малых омических потерь и малого влияния диамагнетизма токов Фуко при дополнительном выполнении условия h/R << 1.

Статья в формате PDF

826 KB

вносимая индуктивность

индукция

вихревое электрическое поле

переменный ток

поток магнитного поля

1. Калантаров П.Л., Цейтлин Л.А. Расчёт индуктивностей: справочная книга. – Л.: Энергоатомиздат, 1986. – 488 с.

2. Манжула В.Г. Исключение структурной, функциональной и схемотехнической избыточности при синтезе аналоговых систем в корпусе // Научно-технический вестник Поволжья. – 2011. – № 2. – С. 123–127.

3. Манжула В. Г. Функционально интегрированная микроэлектронная система защиты на основе быстродействующего датчика температуры // Датчики и системы. – 2012. – № 7. – С. 18–22.

4. Савельев И.В. Курс общей физики. Т.2. – М.: Наука, Главная редакция физико-математической литературы, 1988. – 496 с.

5. Сапогин В.Г., Крутчинский С.Г., Прокопенко Н.Н., и др. Интегральные индуктивности и трансформаторы аналоговых микросхем СВЧ – диапазона. – Шахты: ГОУ ВПО «ЮРГУЭС», 2010. – 273 с.

6. Сапогин В.Г., Марчук В.И., Манжула В.Г. Промежуточный отчёт по гранту РФФИ «Теоретические основы проектирования интегральных индуктивностей для сложных функциональных блоков и IP – модулей систем связи и телекоммуникаций нового поколения». Проект № 12-08-00654а. 2012. – 79 с.

7. Сапогин В.Г., Прокопенко Н.Н., Марчук В.И., Манжула В.Г. Погонная индуктивность цилиндрических проводников с аксиальной плотностью тока // Инженерный вестник Дона. – 2012. – № 4. – www.ivdon.ru/magazine/ archive / n4t1y2012/1264.

8. Aoki et al. USPAP. Distributed circular geometry power amplifier architecture. US 2005/0030098 A1; feb. 10, 2005.

9. El-Sharawy. USP. Monolithic balanced RF power amplifier. US 6, 424, 227 B1; jul. 23, 2002.

10. Lee et al. USPAP. Systems and method for power amplifiers with voltage bousting multi-primary transformers. US 2008/0164941 A1; Jul. 10, 2008.

11. Komijani et al. USPAP. Reconfigurable distributed active transformers. US 2003/0169113 A1; Sep. 11, 2003.

12. Sanderson. USPAP. High Q monolithic inductors for use in differential circuits. US 2006/0220737 A1; Oct. 5, 2006

Современные планарные технологии создания индуктивностей или трансформаторов в частотном диапазоне до 10 Ггц используют геометрию квадрата либо октаэдра [8–10]. Но технология многоугольников обладает одним существенным недостатком: при скачкообразном изменении ориентации токопровода в пространстве скин-эффект создаёт благоприятные условия для выбрасывания электрического заряда на подложку. Применение кольцевой геометрии должно ослабить выбрасывание электрического заряда на подложку и тем самым позволит увеличить на указанных частотах как параметр добротности, так и коэффициент передачи трансформаторов [2, 3].

Известные методы расчёта индуктивностей [1] в микрометровом диапазоне геометрических размеров могут приводить к отрицательным значениям индуктивности. Этот недостаток геометрической теории потребовал создания принципиально новых электродинамических физико-математических моделей, которые ориентированы на потребности планарной микросхемотехники.

В [5–7] был найден подход к решению задач кольцевой геометрии, в основе которого лежит закон Био‒Савара‒Лапласа либо уравнения магнитостатики. Полученные там результаты дают неплохое совпадение с экспериментальными данными и могут быть применимы для частот переменного тока, при которых отсутствует фазовый сдвиг между током и потоком.

Ниже излагается оригинальный подход к решению задач цилиндрической геометрии, в которых между током и потоком может существовать конечный фазовый сдвиг. Подход объединяет в себе возможности двух- и трёхмерных задач и не ограничивает возможный диапазон изменения частоты переменного тока.

Физико-математическая модель расчёта

Предположим, что сплошной проводящий немагнитный цилиндр находится во внешнем однородном переменном магнитном поле, направленном по оси z, 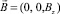. Его зависимость во времени имеет вид

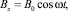(1)

где B0 = const не зависит от цилиндрических координат системы и ограничено в радиальном направлении внешним радиусом цилиндра R, а в аксиальном направлении произвольной высотой цилиндра, обозначенной через h.

При такой ориентации переменное магнитное поле может порождать в цилиндре вихревое электрическое поле, напряженность которого 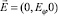имеет одну компоненту. Впервые экспериментальное доказательство существования такой возможной ориентации вихревого электрического поля было обнаружено при создании бетатронов – индукционных ускорителей электронов. В них как раз ускорение электронов и осуществляется вихревым электрическим полем, силовые линии которого представляют собой концентрические окружности. Они формируются электромагнитом специальной формы (см., например, [4]).

Компоненты полей связаны между собой первым уравнением Максвелла, записанным в проекциях

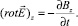(2)

Полагая в (2), что фаза вихревого электрического поля совпадает по фазе со скоростью изменения магнитного поля

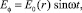(3)

из уравнения (3) получим уравнение, связывающее E0(r) и B0,

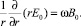(4)

Его решение для E0(r) имеет вид

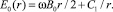(5)

В решении (5) избавимся от особенности при r → 0, полагая C1 = 0. Это условие приводит к тому, что при B0 = 0 E0 = 0. Из (2) видно, что азимутальная компонента вектора напряженности вихревого электрического поля – линейная функция радиуса r с масштабом

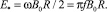(6)

В масштабе напряжённости учтено соотношение ω = 2πf. Тогда (5) с учётом (6) имеет вид

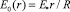при 0 ≤ r ≤ R. (7)

Вихревое электрическое поле в проводящем цилиндре создает вихревые токи Фуко, плотность тока которых имеет такое же направление в пространстве 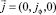. Плотность токов Фуко рассчитывается из дифференциального закона Ома

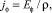(8)

где r – удельное электрическое сопротивление проводящего цилиндра.

Из (8) видно, что плотность тока Фуко в однородной проводящей среде r = const также является линейной функцией радиуса и также зависит от времени, как и Eφ

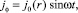(9)

где j0(r) связано с масштабом плотности тока

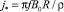(10)

соотношением

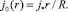(11)

Из соотношения (10) видно, что при прочих равных условиях масштаб тока может достигать больших значений на высоких частотах для проводящей среды с малым значением удельного сопротивления r. Это будет приводить к нагреву проводящего цилиндра на высокой частоте.

Удельная тепловая мощность, выделяемая в локальной области проводника при протекании токов Фуко, рассчитывается из закона Джоуля Ленца:

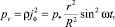(12)

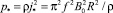где (13)

‒ масштаб объемной плотности тепловой мощности.

Как видно из (13), удельная мощность уже пропорциональна квадрату частоты и для проводящей среды с произвольным значением удельного сопротивления оказывается наиболее значительным на внешней границе цилиндра. Это может приводить к выгоранию его внешней боковой поверхности на высокой частоте.

Тепловая мощность, выделяемая во всём цилиндре, находится из (12)

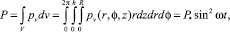(14)

где масштаб тепловой мощности имеет вид

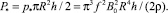(15)

Вихревой ток, индуцированный во всём цилиндре, может быть получен из интегрирования потока

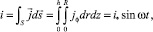(16)

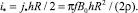где (17)

‒ масштаб индукционного тока.

Частичный учёт магнитных свойств токов Фуко

Вихревая плотность токов Фуко (9) создаёт в пространстве цилиндра собственное магнитное поле 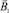. Это магнитное поле отклика вещества для исходной ориентации вихревых токов в цилиндрической системе координат имеет две проекции B1r и B1z. Направление проекции B1z во всех точках цилиндра противоположно внешнему магнитному полю В0. Предполагая, что компонента B1r не зависит от координаты z, распределение собственного магнитного поля можно рассчитать из второго уравнения Максвелла, записанного в проекциях (частная производная компоненты B1r по переменной z опущена):

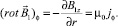(18)

Интегрируя (18) для начального условия B1z(0) с учётом (9), получим

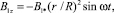(19)

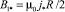где (20)

‒ масштаб индукции собственного магнитного поля. Его можно связать с индукцией внешнего магнитного поля безразмерным параметром β

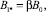(21)

который указывает на влияние диамагнетизма токов Фуко

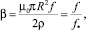(22)

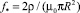где (23)

– масштаб частоты системы. Из (22) видно, что диамагнетизм слабо проявляет себя при b → 0 и его влияние велико на высоких частотах, когда b >> 1. При значении b = 1 масштабы индукций магнитных полей одинаковы.

Поскольку современные материалы от проводников до собственных полупроводников имеют удельное сопротивление, изменяющееся в диапазоне 15,5 нОм·м < ρ < 2,3 кОм·м, то формула для расчета масштаба частоты (23) даёт широкие возможности для ее изменения.

В табл. 1 приведены значения масштаба частоты для восьми проводящих материалов.

Таблица 1

Масштаб частоты для материалов с различным удельным сопротивлением для радиуса цилиндра R = 2 мм.

Как видно из табл. 1, масштаб частот современных материалов лежит в широком диапазоне частот от 2⋅103 до 3⋅1014 Гц.

Энергетический баланс системы

Средняя за период Т изменения поля магнитная энергия, поступающая в цилиндр, находится из интегрирования

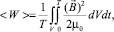(24)

где результирующая индукция магнитного поля системы

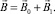(25)

Тогда < W > состоит из двух слагаемых: средней за период энергии внешнего поля

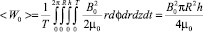(26)

и средней энергии магнитного поля отклика вещества

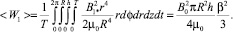(27)

Интегрирование за период скалярного произведения 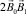обращается в нуль из-за наличия фазового сдвига π/2 между индукциями B1 и B0. В связи с этим между переменными полями B1 и B0 возникает своеобразная интерференция, которая и суммирует обе энергии

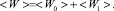(28)

Вносимая за период магнитная энергия (28) расходуется на нагрев проводящего цилиндра Wq и ту часть энергии, которая запасается в индуктивность системы

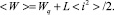(29)

Заметим, что в соотношении (29) не учтена магнитная энергия, которая поставляется в систему радиальной компонентой магнитного поля отклика вещества B1r. Её влияние на процессы дополнительной генерации энергии магнитного поля в пространстве проводящего цилиндра будут учтены в отдельной работе.

Тепловая энергия, расходуемая на нагрев цилиндра за период, вычисляется интегрированием по времени (14)

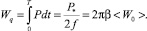(30)

Среднее за период значение квадрата тока найдём из (16)

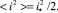(31)

Индуктивные свойства сплошного немагнитного цилиндра

Подставляя в (28) и (29) вычисленные энергии, получим для приведённой индуктивности цилиндра соотношение

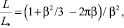(32)

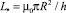где (33)

‒ масштаб индуктивности, который может принимать большие значения для аксиально тонких плёнок при выполнении условия h/R << 1.

Как видно из (32), индуктивность проводящего цилиндра обращается в нуль на двух характеристических частотах F1 и F2 (F1 < F2):

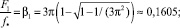(34)

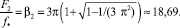(35)

Нули индуктивности делят весь частотный интервал на три части: низкочастотный (выполнено условие 0 < β < β1), среднечастотный, в котором индуктивность принимает отрицательные значения (выполнено условие β1 < β < β2) и высокочастотный, в котором она снова принимает положительное значение (выполнено условие β2 < β < ∞).

Как видно из (32), в низкочастотном диапазоне индуктивность при β → 0 (диамагнетизм токов и омические потери небольшие) может принимать положительные, большие по сравнению с масштабом значения, зависящие от частоты по закону

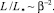(36)

Этот результат представляет интерес для создания больших индуктивностей на низких частотах в малом объёме. При b << 1 формула (36) переходит в формулу

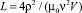(37)

и определяет низкочастотные пределы применимости полученных в ней результатов.

Оценки вносимой индуктивности цилиндра в низкочастотной области

Исследуем возможности увеличения индуктивности в низкочастотной области за счёт уменьшения частоты переменного поля f.

Сплошной цилиндр из марганцовистой латуни будет иметь положительную индуктивность (r = 2,12⋅10–7 Ом×м, (см. табл. 2)) при геометрических размерах R = 2 мм, h = 1 см (выполнено условие h/R > 1). Масштаб частоты f* = 2,69⋅104 Гц. Масштаб индуктивности L* = 1,58 нГн. Первый нуль индуктивности находится на первой характеристической частоте F1 = 0,1605f* = 4,3 кГц. Приведём значения индуктивности цилиндра, которые могут быть реализованы на частотах, меньших первой характеристической частоты в целое число раз.

Таблица 2

Зависимость индуктивности от частоты для условия h/R > 1.

Как видно из табл. 2, увеличение индуктивности за счёт уменьшения омических потерь и влияния диамагнитных свойств токов Фуко может быть в сорок пять раз больше в диапазоне изменения частоты переменного магнитного поля от 0,43 до 2,15 кГц.

Сделаем оценки индуктивности, представляющие интерес для планарных технологий, при выполнении условия h/R << 1. Для тонкой плёнки h = 1 мкм и радиусом R = 1 см, выполненной из электронного кремния (см. табл. 3), имеем: масштаб частоты f* = 5,07⋅1010 Гц. Масштаб индуктивности L* = 39,5 нГн. Первый нуль индуктивности находится на первой характеристической частоте F1 = 0,1605f* = 8,14 ГГц. Приведём значения индуктивности цилиндра, которые могут быть реализованы на частотах, меньших первой характеристической частоты в целое число раз в диапазоне от 0,81 Ггц до 4,07 Ггц.

Применение плёнки из того же материала с той же толщиной, но радиусом в 1 см даёт масштаб частоты f* = 5,07⋅106 Гц. Масштаб индуктивности L* = 0,39 мГн. Первый нуль индуктивности находится на первой характеристической частоте F1 = 0,1605f* = 0,81 МГц. Значения индуктивности изменяются в диапазоне от 30 мГн до 1,4 Гн в интервале изменения частоты от 81 кГц до 0,4 МГц.

Таблица 3

Зависимость индуктивности от частоты для условия h/R << 1

Выводы

• Предложен аналитический метод расчёта индуктивных свойств сплошного проводящего немагнитного цилиндра произвольной высоты и радиуса с азимутальной плотностью вихревого тока при наличии омических потерь и диамагнитных свойств токов Фуко.
• Получены радиальные распределения азимутальной компоненты напряжённости вихревого электрического поля, плотности токов Фуко и удельной тепловой мощности, выделяемой в локальной области проводящего цилиндра.
• Из энергетических соображений получена формула для вычисления вносимой индуктивности сплошного проводящего цилиндра.
• Показано, что индуктивность проводящего цилиндра обращается в нуль для двух характеристических частот F1 и F2.
• Нули индуктивности делят интервал частот на три части: низкочастотный, среднечастотный и высокочастотный.
• На низких и высоких частотах индуктивность проводящего цилиндра принимает положительные значения, а на средних частотах индуктивность отрицательна.
• Показано, что вносимая индуктивность зависит от частоты и имеет большие абсолютные значения в диапазоне низких частот.
• Оценки, проведённые для латунного цилиндра в диапазоне низких частот, при выполнении условия h/R > 1 указывают на то, что больших положительных значений индуктивности латуни на уровне 1 мкГн, отличающихся в 45 раз, можно добиться в интервале частот от 0,43 кГц до 2,15 кГц.
• Оценки, проведённые для плёнки из электронного кремния в диапазоне низких частот, при выполнении условия h/R << 1 указывают на то, что больших значений индуктивности на уровне 50 мкГн, отличающихся в 45 раз, можно добиться в интервале частот от 0,81 ГГц до 4,07 ГГц.

Работа выполнена при поддержке Российского фонда фундаментальных исследований, грант № 12-08-00654/12 (2012-2013 гг.).

Рецензенты:

Бубнов В.А., д.т.н., профессор, заведующий кафедрой естественнонаучных дисциплин, ГБОУ ВПО «Московский городской педагогический университет», г. Москва;

Крутчинский С.Г., д.т.н., профессор кафедры систем автоматического управления, ФГАОУ ВПО «Южный федеральный университет», г. Ростов-на-Дону.

Работа поступила в редакцию 16.12.2013.

Библиографическая ссылка