Многолетняя практика эксплуатации резервуаров показывает, что имеются случаи разрушения металлоконструкций РВС в узле сопряжения стенки и днища. Это ведет к утечке нефти и, как следствие, к значительным материальным затратам, а также наносится вред экологии. Поэтому исследования неравномерных осадок наружного контура днища и окрайки, оценка напряженно-деформированного состояния стенки в зоне нижнего узла позволят обеспечить повышение эксплуатационной надежности вертикальных стальных резервуаров. Однако существующие аналитические методы не позволяют учесть физическую и геометрическую нелинейность при расчете НДС конструкций, поэтому для получения более точных результатов, авторами предлагается использовать метод конечных элементов. Таким образом, предполагается получить численную модель резервуара, максимально отражающую нелинейность, возникающую при воздействии различных факторов, представленных ниже.
В настоящее время эксплуатируется большое количество резервуаров с имеющимися отклонениями от проектной геометрии и дефектами в области нижнего узла, появившихся в результате различных факторов. С момента ввода в эксплуатацию большинства резервуарных парков Западной Сибири изменилась технологическая схема перекачки нефти. Факторами изменения НДС резервуара в области сопряжения стенки и окрайки являются ошибки в проектировании и строительстве. Так, раньше изыскания включали в себя бурение только одной скважины для получения данных об инженерно-геологическом строении грунтового основания под строительство резервуара. Это приводило к снижению точности расчета основания и фундамента. В настоящее время инженерно-геологические изыскания включают в себя бурение минимум 5 скважин. Также произошли изменения в нормативных величинах ветровой и снеговой нагрузок, поэтому многие резервуары, изначально рассчитанные для одних ветровых и снеговых районов, перестали выполнять условие прочности и устойчивости для новых нормативных значений. На напряженно-деформированное состояние нижнего узла резервуара также могут влиять изменения в свойствах металла (хрупкости, прочности, пластичности), обусловленные длительным сроком эксплуатации и колебаниями температур. Районы эксплуатации резервуаров характеризуются сложными грунтовыми условиями: заболоченность территории, наличие слабых водонасыщенных грунтов, что увеличивает вероятность возникновения неравномерных осадок резервуарных конструкций.
Вопросы неравномерных осадок наружного контура днища РВС рассматриваются в трудах [1, 2, 3]. В их работах получены подробные аналитические решения по данной проблеме. Вопросы напряженно-деформированного состояния конструкций резервуаров широко описаны в трудах [4, 5, 6]. Теория цилиндрической оболочки подробно представлена в [7]. Расчетная схема в общем случае, в которой описываются действующие нагрузки в области нижнего узла резервуара, представлена на рис. 1.
Общее дифференциальное уравнение изгиба замкнутой круговой цилиндрической оболочки, находящейся под действием осесимметричной гидростатической нагрузки, выглядит следующим образом:
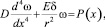 (1)
(1)
где D – цилиндрическая жесткость; E – модуль упругости для стали; δ – толщина стенки; r – радиус резервуара; x – координата высоты прогиба; ω – значение прогиба в радиальном направлении; P(x) – интенсивность внешней нагрузки.
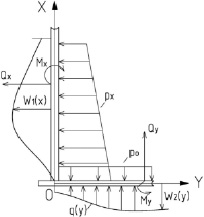
Рис. 1. Расчетная схема нижнего узла резервуара: W1(x) – радиальное перемещение стенки; W2(y) – вертикальное перемещение днища; px = p0(1 – x/H) – давление жидкости на отметке x; p0 – давление жидкости на отметке x = 0; q(y) – реактивный отпор грунта под днищем; Мx, My, Qx, Qy – изгибающие моменты и поперечные силы в стенке и днище
Частным интегралом приведенного выше уравнения с учетом граничных условий является уравнение прогибов стенки по [6]:
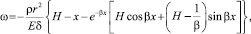 (2)
(2)
где ρ – плотность нефтепродукта; H – высота резервуара; β – коэффициент деформации стенки.
Дифференциальные уравнения и их аналитические решения получены для осесимметричного случая нагружения идеальной цилиндрической оболочки гидростатическим давлением без учета физической и геометрической нелинейности материала конструкции. Для исследования процессов развития неравномерной осадки резервуаров для хранения нефти предлагается использовать численные методы расчета, реализованные в программном комплексе ANSYS. Однако для дальнейшего использования модели резервуара в расчетах необходимо убедиться в адекватности созданной модели.
Автором предлагается решить численным методом рассмотренную выше аналитическую задачу при осесимметричном нагружении в линейной постановке. Таким образом, будет проверена предлагаемая расчетная схема и конечно-элементная модель, которую можно будет использовать в дальнейшем для решения более сложных задач в неосесимметричной постановке.
Расчетная схема (рис. 2) включает в себя действие гидростатической, ветровой нагрузок, а также учитывается вес снегового покрова, кровли. В предложенной модели принимается условие абсолютно жесткого защемления стенки в уторном шве (fixedsupport), кровля не защемлена.
Геометрическая модель резервуара строилась в соответствии со значениями, принятыми в типовом проекте для РВС-20000 (ТП 704-1-60). Радиус резервуара составляет 22,85 м, высота стенки 11,92 м. Толщина стенки для первого пояса – 13 мм, для 2–8 поясов – 11 мм. Листы стенки выравниваются по внутреннему краю. Для задания гидростатической нагрузки выбраны следующие параметры: высота взлива нефти hвз = 10,88 м, плотность хранимой нефти ρ = 875 кг/м3, значение гравитационной постоянной принимается 8,91 кг/м·с2. Значение ветрового давления принимается в соответствии с СП 20.13330.2011 для I ветрового района qветр = 230 Па. В предложенной расчетной схеме не моделируется конструкция кольца жесткости и кровли, но для получения достоверных результатов их вес необходимо учитывать. Равномерно распределенная нагрузка от веса кровли, снега, оборудования кровли, кольца жесткости (q) составляет 1200 кН. Данная сила приложена по нормали к верхнему ребру стенки РВС. Отметим, что все силы, рассмотренные в расчетной схеме, прикладываются одновременно.
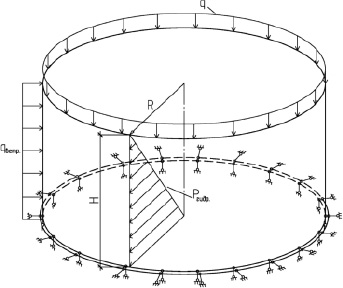
Рис. 2. Расчетная схема резервуара: Pгидр – гидростатическое давление на стенку и днище резервуара; qветр – ветровая нагрузка; q – нагрузка от веса металлоконструкций кровли, снега; R – радиус резервуара; H – высота резервуара
Материал металлоконструкций – сталь конструкционная низколегированная 09Г2С с пределом текучести σ0,2 = 300 МПа.
Для построения конечно-элементной сетки выбран элемент SHELL181 (рис. 3), имеющий ряд особенностей, присущих тонкостенным оболочкам, к которым относится конструкция стенки РВС.
Элемент SHELL181 имеет свойства линейной упругости, упругопластичности материала. Из упругих материалов могут применяться изотропные, анизотропные и линейные ортотропные. Пластическое поведение предполагает упругие изотропные свойства материала (то есть если ортотропный материал подвергается пластическому деформированию, комплекс ANSYS будет использовать изотропный материал с модулем Юнга Е и коэффициентом Пуассона). Элемент SHELL181 учитывает влияние поперечных сдвиговых деформаций. На рис. 3 изображен конечный элемент SHELL181, обозначено 8 узловых точек и 6 степеней свобод элемента в ортогональной системе координат XYZ. Плотность генерируемой сетки влияет на погрешность в вычислениях, поэтому определение оптимальных параметров сетки во многом определяет точность расчетов. В узле сопряжения стенки и днища автором предлагается сгущать конечно-элементную сетку 0,1 м (сторона квадрата элемента SHELL181).
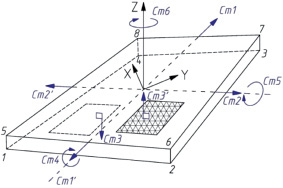
Рис. 3. Конечный элемент SHELL181: Ст1-Ст6 – обозначение степеней свободы; 1–8 – узловые точки
В постпроцессорной обработке результатов получены значения эквивалентных напряжений и матрица перемещений. Распределение напряжений в стенке резервуара РВС-20000 по высоте представлено на графике (рис. 4).
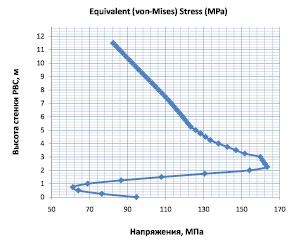
Рис. 4. Напряжения, возникающие в стенке резервуара при действии эксплуатационных нагрузок
Если проанализировать график на рис. 4, то можно сделать вывод о том, что с точки зрения теории прочности скачок напряжений на высоте h = 0,5–3 м объясняется моментным напряженно-деформированным состоянием конструкции стенки. Максимальные напряжения находятся на высоте 2,5 м и составляют 165 МПа. Перемещения стенки в радиальном направлении по высоте от действия эксплуатационных нагрузок изображены на графике (рис. 5).
На графике дополнительно нанесено решение для прогибов, полученных из аналитического выражения (2).
Выводы
– Авторами получена численная модель резервуара, позволяющая выполнять расчеты НДС конструкций в неосесимметричной постановке с учетом физической и геометрической нелинейности.
– Проверена адекватность предложенной модели, разница результатов задачи в осесимметричной постановке, решенной аналитическим и численным методами, составляет 1,76 %. Таким образом, предложенную модель можно считать адекватной, т.к. отличие от аналитического решения составило не более 2 %.
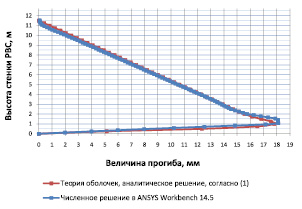
Рис. 5. Перемещения стенки в радиальном направлении от действия эксплуатационных нагрузок
– Данная расчетная схема и полученная модель будут использованы автором для более сложных исследований, а именно для расчета неравномерной осадки резервуаров в неосесимметричной постановке.
Рецензенты:Обухов А.Г., д.ф-м.н., профессор кафедры «Высшая математика», ФГБОУ ВПО «Тюменский государственный нефтегазовый университет», г. Тюмень;
Мерданов Ш.М., д.т.н., профессор, зав. кафедрой «Транспортные и технологические системы», ФГБОУ ВПО «Тюменский государственный нефтегазовый университет», Почетный работник высшего профессионального образования Российской Федерации, г. Тюмень.
Работа поступила в редакцию 05.12.2013.
Библиографическая ссылка
Тарасенко А.А., Чепур П.В., Чирков С.В., Тарасенко Д.А. МОДЕЛЬ РЕЗЕРВУАРА В СРЕДЕ ANSYS WORKBENCH 14.5 // Фундаментальные исследования. 2013. № 10-15. С. 3404-3408;URL: https://fundamental-research.ru/ru/article/view?id=33075 (дата обращения: 07.03.2026).



