Предположим, исследуется сложная техническая система, которая за заданное время должна достигнуть заданного состояния (положения). Определим риск как степень угрозы недостижения поставленной цели, что может привести к потере управляемости всей системы. Риск будет рассматриваться как переменная величина, представляющая собой функцию относительно текущего положения системы. Риск будет увеличиваться при приближении системы к некоторым допусковым границам, после достижения которых система становится неуправляемой.
Такая трактовка риска приводит к введенной Гильбертом и Клейном проективной метрике на плоскости Лобачевского–Клейна. Плоскость Лобачевского–Клейна представляет собой единичный круг, любая хорда которого трактуется как бесконечная прямая (рис. 1).
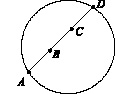
Рис. 1. Плоскость Лобачевского–Клейна
Расстояние ρ(B, C) между точками B и C стремится к бесконечности при C → D или при B → A. Это расстояние задается формулой ![]() , где
, где ![]() – ангармоническое отношение четырёх точек.
– ангармоническое отношение четырёх точек.
Выражения, аналогичные проективному расстоянию, присутствуют и в нечеткой логике при описании операторов нечёткой импликации, которые возникают при оценке осуществимости вывода о том, что при выполнении определенных условий можно получить требуемый результат.
И, главное, проективное расстояние имеет очевидные аналогии с d-оценками (оценками «трудности» Руссмана) [1], которые в данном исследовании и предлагается использовать для количественной оценки риска потери управляемости системы.
Математическое моделирование оценок риска
D-оценкой (или «трудностью» Руссмана) называется величина, задаваемая соотношением
![]() , (1)
, (1)
где μ ≥ ε, ε ∈ [0, 1), μ ∈ (0, 1].
Очевидно, что d ∈ [0, 1]. Кроме того, d = 0 когда ε = 0 или μ = 1. Трудность максимальна (d = 1) при μ = ε.
Формула (1) имеет следующую вероятностную интерпретацию. Введем два случайных события: A за заданное время система не достигла планового состояния, В – величина изменения контролируемого параметра системы вышла за допусковые границы. Тогда d выступает как вероятность ![]() недостижения результата в случае, если контролируемый параметр удовлетворяет требованиям. При этом величины ε и μ допускают одну из двух возможных интерпретаций:
недостижения результата в случае, если контролируемый параметр удовлетворяет требованиям. При этом величины ε и μ допускают одну из двух возможных интерпретаций:
1. ε = p(B); μ = p(B/A) или
2. ![]() ,
, ![]() .
.
В том и другом случае естественно предполагается выполнение условия p(B/A) = 1, то есть если величина изменения контролируемого параметра системы вышла за допусковые границы, результат всегда не достигается.
Действительно, убедимся в справедливости, например, первой интерпретации. Найдем
![]()
По условию,
![]()
Таким образом, должно выполняться равенство
![]()
или
![]() .
.
По теореме произведения вероятностей
p(AB) = p(A)p(B/A) = p(B)p(A/B) = p(B)
(т.к. p (A/B) = 1). То есть p(A)p(B/A) = p(B), что и требовалось показать.
Оценки вида (1), рассчитанные на основе геометрической интерпретации движения системы, могут быть использованы для характеристики риска недостижения системой цели. В частности, появляется возможность решить следующие две задачи прогнозирования технического состояния:
– мониторинг риска во время движения системы по траектории;
– определение порогового значения риска потери управляемости, превышение которого признается нежелательным.
Очевидно, что такие параметры, как максимальная и минимальная скорость движения системы, определяются на этапе конструирования системы. Таким образом, помимо естественных задач мониторинга текущего значения риска могут быть поставлены еще и более общие задачи:
– для заданной системы определить плановую конструкторски допустимую траекторию движения к цели чтобы минимизовать максимальный уровень возможного риска;
– либо обратный случай: построить такую модель системы, чтобы риск, трактуемый как угроза потери управляемости системы, при движении системы по некоторой фиксированной плановой траектории A = f(t) был минимален.
Целью во всех случаях будет являться достижение системой состояния Аpl за время tpl.
На рис. 2 траектории движения системы с минимальной допустимой скоростью соответствует прямая OD, траектории движения с максимальной допустимой скоростью ‒ прямая OB. Кривая A = f(t) – некоторая плановая траектория движения системы к цели C.
Если в процессе движения объект оказывается правее прямой СD, то достижение цели в заданное время становится невозможным, так для этого необходимо движение со скоростью, превышающей максимальную. Поэтому эта область становится запретной, и приближение к ней увеличивает угрозу потери управляемости. Риск, отражающий величину этой угрозы, будет стремиться к единице при приближении точки к прямой СD.
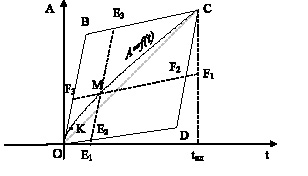
Рис. 2. Графическое представление возможной траектории системы
Также запретной будет считаться область, лежащая ниже прямой ОD, хотя из лежащей там точки теоретически возможно достичь цели в плановый срок. Тем не менее минимальная скорость будет пониматься нами как оценка надежности объекта, а движение с еще меньшей скоростью интерпретироваться как возникновение чрезвычайных обстоятельств, которые могут привести к возникновению аварийной ситуации.
Таким образом, ломаная ODC на рис. 2 является границей запретной области. За величину риска для точки М с координатами (t, A) принимается величина
![]()
где ![]()
![]()
При этом
![]()
![]()
![]()
![]()
В соответствии с принятой интерпретацией, d1 и d2 ‒ это две различные условные вероятности недостижения поставленной цели, a 0 ≤ r ≤ 1 – риск потери управления, посчитанный на основе этих вероятностей.
Если перейти к безразмерным величинам и положить Apl и tpl равными единице, то формулы вычисления d-оценок в точке произвольной траектории (t0, f(t0)) будут иметь следующий вид:
![]() (2)
(2)
![]() (3)
(3)
В полученных формулах f(t) представляет собой плановую траекторию движения системы к цели, где f(t) – произвольная функция.
Анализ оценок риска
Формулы (2) и (3) позволяют исследовать свойства оценок риска r(t) для некоторых классов плановых траекторий.
В частности, проанализируем траектории Γf поведения системы в плановом периоде, имеющие вид двухзвенной ломаной:
![]()
где ![]() – точка перехода траектории с первого звена на второе.
– точка перехода траектории с первого звена на второе.
Иначе говоря, предполагается, что до некоторого момента t0 система движется к цели с постоянной скоростью k3, а после этого момента она движется с постоянной скоростью k4 ≠ k3.
Если решается задача определения плановой конструкторски допустимой траектории движения к цели, минимизирующей уровень возможного риска, то можно показать [2], что для практического использования наиболее подходят траектории, для которых выполняется равенство
![]()
В этом случае t0 = t1 = t2, и в этой точке принимается значение min r(t) – наименьшее значение риска r(t) на траектории Γf, которое равно
![]()
Таких траекторий – бесчисленное множество (в плоскости k3Ok4 они задаются частью гиперболы вида ![]() ), поэтому этот класс предоставляет достаточно широкие возможности для принятия решения о выборе траектории движения системы к цели. В частности, в этот класс попадают как траектории, для которых k3 < k4 (система вначале движется с более высокой скоростью, а потом с более низкой), так и траектории, для которых k3 > k4.
), поэтому этот класс предоставляет достаточно широкие возможности для принятия решения о выборе траектории движения системы к цели. В частности, в этот класс попадают как траектории, для которых k3 < k4 (система вначале движется с более высокой скоростью, а потом с более низкой), так и траектории, для которых k3 > k4.
Для траекторий, относящихся к классу функций f(t) = tα, α > 0, наилучшие показатели риска достигаются при α = 0.
В данной ситуации появляется возможность естественной трактовки d1(t) и d2(t) как функции принадлежности нечетких лингвистических критериев, задающих границы попадания системы в аварийное состояние, при этом ![]() будет нечеткой суммой таких критериев
будет нечеткой суммой таких критериев
![]()
![]()
![]()
Рассмотрим возможные значения данного максимума на промежутке t ∈ [0, 1]. Для этого изобразим графически функции d1(t) и d2(t) (рис. 3).
Очевидно, что
![]()
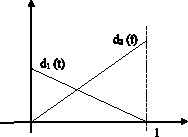
Рис. 3. Графическое представление изменения оценок риска
Если перейти на следующий уровень оптимизации и рассмотреть задачу построения такой модели системы, чтобы риск при движении системы по фиксированной плановой траектории f(t) = t был минимален, то наилучшей относительно введенной нами оценки риска будет система, параметры которой удовлетворяют равенству: k1k2 = 1. При этом из возможных конструкторских решений нужно выбирать то, для которого значение k1 минимально. Отметим, что для такой системы максимум оценки риска будет представлять представляет собой минимум из всех возможных максимумов r(t) не только по траекториям вида f(t) = tα, α > 0, но и по траекториям, представляющим собой двузвенные ломаные.
Заключение
Таким образом, в статье получены и исследованы формулы, выражающие оценку величины риска, трактуемого как угроза потери управляемости системы в задаче для нескольких (наиболее естественных) классов возможных траекторий поведения системы в зависимости от текущего положения системы и значений допусковых границ.
Рецензенты:Азарнова Т.В., д.т.н., профессор, Воронежский государственный университет, г. Воронеж;
Шашкин А.И., д.ф.-м.н., профессор, декан факультета прикладной математики, информатики и механики, Воронежский государственный университет, г. Воронеж.
Работа поступила в редакцию 05.12.2013.
Библиографическая ссылка
Львович Я.Е., Каширина И.Л. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ОЦЕНОК РИСКА ДОСТИЖЕНИЯ ДОПУСКОВЫХ ГРАНИЦ В ПРОЦЕССЕ ИСПЫТАНИЙ ТЕХНИЧЕСКИХ СИСТЕМ // Фундаментальные исследования. 2013. № 10-15. С. 3347-3351;URL: https://fundamental-research.ru/ru/article/view?id=33064 (дата обращения: 30.12.2025).



