По определению, балансовая древесина (балансы) – круглые лесоматериалы в виде отрезков ствола дерева, имеют длину, например, 1–3 м и диаметр 8–24 см. Балансы необходимы для производства целлюлозы.
В данной работе используется геометрическая модель баланса в виде прямого кругового цилиндра.
Очистка от коры является необходимым звеном в технологии подготовки круглых лесоматериалов к их дальнейшему использованию. Крупным потребителем круглых лесоматериалов является целлюлозно-бумажная промышленность, где требуется наиболее высокая степень очистки от коры. Развитие технологий очистки круглых лесоматериалов от коры отражено в работах [1, 8–12]. В целлюлозно-бумажной промышленности технология очистки древесины в корообдирочных барабанах остаётся доминирующей [8–12, 20–22], развиваясь параллельно с роторной [1, 6] и другими технологиями окорки [7, 17].
Большой объем экспериментальных и теоретических исследований по очистке древесины от коры был выполнен в 1970-е годы [21]. Обобщение полученных в эти годы результатов с учетом выполненных до 1980 г. работ, начиная с работы Б.Г. Залегаллера (1949), приведено в монографии С.П. Бойкова [1].
В данной работе рассматривается одна из проблем, источник которой – объективно существующее противоречие требования высокой степени очистки от коры, с одной стороны, и, с другой стороны, необходимости уменьшения потерь древесины при окорке.
Высокая степень очистки балансов от коры достигается увеличением продолжительности их обработки в барабане. Однако в этом случае с течением времени возрастает число ударов по очищенной от коры поверхности баланса, что ведет к разрушению и потерям древесины. Поэтому необходим компромисс между потерями древесины и степенью очистки от коры [1, 5, 7–9].
Согласно [21], потери древесины при очистке в корообдирочных барабанах могут составлять от 1 до 4 %. Это больше, чем при хранении круглых лесоматериалов (от 0,1 до 0,5 %), измельчении на щепу и сортировке щепы (от 0,5 до 2,5 %), транспортировке щепы (от 0 до 0,5 %), хранении щепы (от 0,1 до 1,5 %). Некоторые предложения по уменьшению потерь древесины рассмотрены в статьях [10, 13, 15].
Цель данной работы – исследование закономерностей соударений и качества очистки от коры круглых лесоматериалов неодинакового диаметра в корообдирочных барабанах.
Материалы и методы исследования
Многочисленные факторы, влияющие на качество очистки от коры, можно свести к двум параметрам – количеству ударов и силе контактного взаимодействия при соударениях балансов. Соударения балансов, с учетом стохастичности, рассматриваются в [1] как независимые повторяющиеся испытания по схеме Бернулли. При этом вероятность удара по случайно выбранному участку поверхности баланса равна
![]() (1)
(1)
Здесь ∆S – площадь участка (пятна контакта соударяющихся балансов); S – площадь поверхности баланса. С использованием распределения Пуассона в [1] получена формула для определения вероятности ударов по участку:
p(m ≥ 1) = 1 – e–λt. (2)
Здесь λ – интенсивность соударений (среднее количество ударов по одному участку за единицу времени); t – продолжительность процесса.
Степень очистки от коры принято определять в процентах [21]. Если сила однократного контактного взаимодействия балансов достаточна для разрушения и удаления коры по пятну контакта, то формула (1) определяет зависимость качества окорки от продолжительности обработки и интенсивности соударений λ [1]:
Cdeb = (1 – e–λt)·100 %. (3)
Если для разрушения и удаления коры на рассматриваемом участке необходимо не менее b ударов, то вероятность окорки участка, как показано в [1], равна
![]() (4)
(4)
Качество (степень) окорки в этом случае Cdeb = p(m ≥ b)·100 % .
Результаты исследования и их обсуждение
Рассмотрим геометрические аспекты задачи. В приведенных выше формулах (1)–(4) по умолчанию предполагается, что площадь окоряемой поверхности соударяющихся балансов, а значит, и диаметры одинаковы (если балансы не различаются по длине). Рассмотрим соударение балансов 1 и 2 одной и той же длины L, но неодинакового диаметра, D1 и D2 соответственно. Очевидно, в формуле (1) величина ∆S будет одной и той же для каждого из этих балансов. При этом S1 = πD1L и S2 = πD2L. Согласно (1)
![]()
![]() (5)
(5)
Тогда
![]()
![]() (6)
(6)
Обозначим kD = D1⁄D2 и перепишем формулу для p2 (6) в виде
p2 = p1kD. (7)
С помощью коэффициента kD моделируется влияние только геометрических характеристик и ∆S (5). Формула (6) показывает, что с увеличением диаметра баланса степень его очистки от коры линейно уменьшается. Однако в реальных технологических ситуациях с увеличением диаметра баланса степень очистки уменьшается нелинейно [12]. Это несоответствие указывает на то, что не приняты во внимание некоторые существенные характеристики. Предположим, что такой характеристикой является интенсивность соударений λ в формулах вида (2)–(4). Влияние только изменений интенсивности соударений учтем с помощью некоторого коэффициента kλ. Тогда, моделируя совместное влияние геометрических и физических характеристик на p2 (7), запишем:
p2 = p1kDkλ. (8)
Чтобы определить kλ, обратимся к работе [3], в которой показано, что с уменьшением диаметра балансов количество соударений в единицу времени возрастает (примерно линейно). На этом основании можем записать:
![]()
![]() (9)
(9)
Таким образом, коэффициент kλ = D1⁄D2 равен указанному выше коэффициенту kD. Тогда
![]() (10)
(10)
Правомерность такого подхода к учету влияния интенсивности соударений с помощью коэффициента kλ можно обосновать следующим образом. Примем во внимание, что
![]() (11)
(11)
Тогда зависимости вида (2) можно аппроксимировать линейными соотношениями:
![]()
![]() (12)
(12)
Учитывая (9) и (12), получим:
![]()
![]() (13)
(13)
Формула (13) моделирует влияние только физических характеристик балансов на вероятность их соударений. Совместное влияние изменений геометрических и физических характеристик учитывается произведением коэффициентов kD и kλ в формулах (8), (10).
Необходимо подчеркнуть, что формулы (8) и (10) не предназначены для вычисления вероятности соударений и степени очистки балансов. Эти формулы отражают только качественные характеристики (закономерности) рассматриваемого процесса.
Результаты экспериментов по исследованию влияния диаметра лесоматериалов на качество окорки приведены в [12]. Эти данные с достаточной точностью аппроксимируются полиномом второй степени (рисунок), что подтверждает адекватность формулы (10).
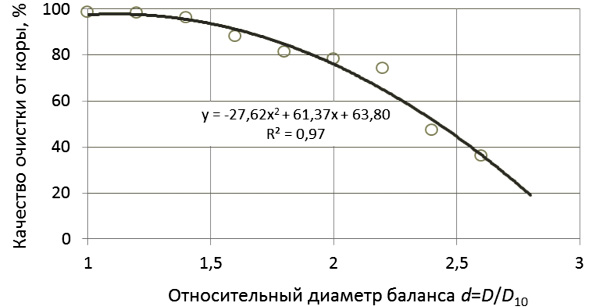
Влияние диаметра баланса на качество очистки от коры, D10 = 10 см
Обсуждение и заключение
Выполненное исследование подтверждает существование закономерности: уменьшение степени очистки от коры пропорционально квадрату увеличения диаметра баланса (10). Поэтому при совместной обработке в корообдирочном барабане балансов неодинакового диаметра более интенсивному воздействию подвергаются балансы меньшего диаметра по сравнению с балансами большего диаметра. Эта закономерность подтверждается известными экспериментальными данными [12] и результатами численного моделирования [3].
Если все балансы будут иметь одинаковый диаметр, то процесс очистки от коры будет наиболее эффективным по затратам времени и по критерию потерь древесины. Объясняется это тем, что площадь боковой поверхности балансов малого диаметра меньше, и, согласно (6) и (7), эти балансы будут освобождены от коры за меньшее число соударений. Очистка же от коры балансов большего диаметра требует, соответственно, большего числа соударений. Если в соударениях участвуют уже очищенные от коры балансы малого диаметра, то разрушается древесина этих балансов. Отсюда следует, что необходимо сортировать балансы по диаметру до загрузки в корообдирочный барабан и обрабатывать балансы в барабане группами, чтобы минимизировать различие диаметров загруженных в барабан балансов.
Работа выполнена в рамках реализации комплекса мероприятий Программы стратегического развития ПетрГУ на 2012–2016 гг.
Рецензенты:
Сюнёв В.С., д.т.н., профессор, директор Института рационального природопользования на Европейском Севере, г. Петрозаводск;
Малинов Г.И., д.т.н., профессор кафедры механизации сельскохозяйственного производства, ФБГОУ ПетрГУ, г. Петрозаводск.
Работа поступила в редакцию 05.12.2013.
Библиографическая ссылка
Колесников Г.Н., Доспехова Н.А. ЗАКОНОМЕРНОСТИ СОУДАРЕНИЙ И КАЧЕСТВО ОЧИСТКИ БАЛАНСОВ НЕОДИНАКОВОГО ДИАМЕТРА В КОРООБДИРОЧНОМ БАРАБАНЕ // Фундаментальные исследования. 2013. № 10-15. С. 3328-3331;URL: https://fundamental-research.ru/ru/article/view?id=33060 (дата обращения: 30.12.2025).



