Разработке инерционных интегрирующих приборов посвящен ряд научных работ [2–6]. Статья [6] посвящена методу многокритериальной оптимизации конструкции магнитного тормоза инерционного прибора (или, как определено в [6], «магнитной системы индукционного демпфера дискового типа, сочетающего в себе возможность плавной регулировки коэффициента индукционного демпфирования»). Ряд патентов и авторских свидетельств [2–5] посвящен конструкции магнитного демпфера и магнитной системы привода с регулируемым тяговым усилием. Однако они нуждаются в дополнении и уточнении для конкретных конструкций приборов и определяющих их параметров. Приведенные материалы являются востребованными при разработке конструкции, но не вполне эффективны при решении задач производства приборов, когда ряд конструктивных параметров уже определен и первоочередной является задача технологической подготовки производства. Поэтому в данной статье предложена математическая модель инерционного акселерометра, которая может быть использована при настройке и регулировке прибора, при его изготовлении. Основными причинами, побудившими авторов к разработке модели, послужили трудности, возникшие при изготовлении и настройке акселерометров.
Конструкция интегрального акселерометра с чувствительным элементом, совершающим вращательное движение, показана на рис. 1, а принцип его работы состоит в следующем. В начальный момент времени чувствительный элемент (4) удерживается в исходном положении силами магнитного взаимодействия первого (1) и третьего (3) устройств регулирования. При воздействии на него силы, обусловленной переносным ускорением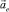 
, в направлении, показанном на рис. 1, и достижении им заданного уровня чувствительный элемент переходит из состояния покоя в состояние движения. Во время движения на чувствительный элемент действуют силы магнитного тормоза (8), предающиеся через зубчатую передачу (7) и второго устройства регулировки (2). Чувствительный элемент находится на одной оси с подвижной контактной группой (4), поэтому происходит коммутация электрических цепей контактов (5) при повороте чувствительного элемента на заданный угол.
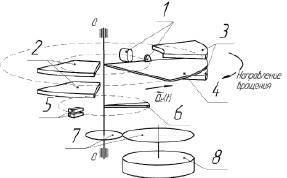
Рис. 1. Инерционный интегрирующий акселерометр с чувствительным элементом, совершающим вращательное движение: 1 – первое устройство регулирования; 2 – второе устройство регулирования; 3 – третье устройство регулирования; 4 – чувствительный элемент; 5 – контакты; 6 – подвижная контактная группа; 7 – зубчатая передача; 8 – магнитный тормоз; О – ось вращения чувствительного элемента
Факторы, учтенные в математической модели
В представленной статье при определении функциональных характеристик акселерометра учтены следующие факторы:
а) закон изменения переносного ускорения;
б) значения нагрузок на чувствительный элемент прибора, определяемых его регулирующими системами (с учетом различных вариантов регулировок и настроек магнитных систем);
в) допуски на геометрические размеры деталей шероховатость поверхностей;
г) отклонения магнитных свойств материалов, применяемых в регулировочных устройствах.
Все перечисленные факторы формируют спектр критичных параметров, оказывающий наиболее сильное влияние на функциональную характеристику прибора при настройке.
Методика расчета
Установлено, что расчет интегрирующего акселерометра можно условно разделить на две части – статическую и динамическую. Для каждого режима работы составлены расчётные схемы. Движение чувствительного элемента акселерометра разделено на секторы, в каждом из которых на него действуют: моменты внешних сил, моменты регулирующих устройств, сил трения. Расчет силовых характеристик регулирующих систем выполнялся с помощью пакетов Ansys, Pro/ENGINEER, с последующей аппроксимацией.
Приведем примеры дифференциальных уравнений, описывающих движение чувствительного элемента в первых двух секторах, и их нагрузочную диаграмму.
1. Первый сектор. Момент индукционного тормоза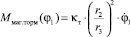 
. Уравнение имеет вид
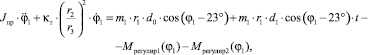(1)
где Jпр − приведенный момент инерции; m1 − масса чувствительного элемента; r1 − расстояние от оси вращения до центра масс чувствительного элемента; d0 − максимальная величина переносного ускорения, при котором чувствительный элемент находится в состоянии равновесия; d1 − скорость нарастания ускорения; Mрегулир 1(φ1) − первого регулирующего устройства; Mрегулир 2(φ1) − второго регулирующего устройства; r2, r3 − радиусы зубчатых колес.
2. Второй сектор. В данном секторе перестает действовать момент Mрегулир 1(φ1). Уравнение имеет вид
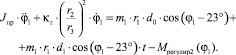(2)
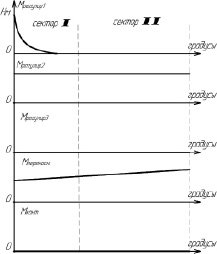
Рис. 2. Диаграмма моментов, приложенных к чувствительному элементу интегрирующего акселерометра, первые два сектора
Приведенные выше уравнения являются нелинейными, поэтому их решение осуществлено численным методом, интегрированным в программу Mathematica [7].
В результате решения уравнений во всех секторах получаем время срабатывания прибора tсраб., а соответственно и скорость его срабатывания 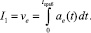(3):
(3)
Анализ
Системный анализ влияния внешних воздействий и конструктивных параметров на функциональные характеристики прибора, выполненный с использованием разработанной математической модели, учитывающей множество критичных конструктивных параметров.
1. Обеспечение постоянства скорости срабатывания при различных законах изменения переносного ускорения
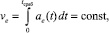
то есть I1 = I2 (рис. 3).
2. Влияние величины зазоров в регулирующих устройствах на величину напряженности поля в рабочих зазорах устройств, и в итоге на время срабатывания акселерометра в целом. Приведем для примера оценку влияния изменения зазоров в третьем регулирующем устройстве на погрешность срабатывания акселерометра табл. 1.
Принцип действия и конструкция третьего регулирующего устройства подробно представлены в [1].
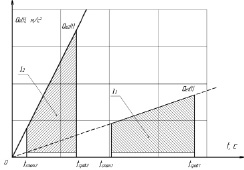
Рис. 3. Диаграмма срабатывания прибора для двух скоростей нарастания ускорения
Таблица 1
Оценка влияния изменения зазоров в третьем регулирующем устройстве на погрешность срабатывания акселерометра
|
Область изменения зазоров |
Погрешность величины скорости срабатывания |
|
|
При минимальном значении |
При максимальном значении |
|
|
Зазор Б3 от 0,2 мм min, В3 0,3 мм min, при этом В3 должен быть больше размера Б3 на 0,1 мм min |
0 % |
3 % |
На рис. 4 показаны зазоры Б3, В3, определяющие момент третьего регулирующего устройства.
3. Оценка влияния допусков на геометрические размеры на время срабатывания прибора. Рассмотрим это на следующем примере.
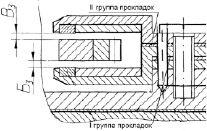
Рис. 4. Зазоры Б3, В3 третьего регулирующего устройства
Связь толщины диска h1 ротора (рис. 5) (в пределах допуска) с параметрами модели и погрешностью срабатывания прибора с использованием разработанных аналитических зависимостей приведена в табл. 2.
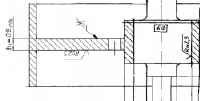
Рис. 5. Допуск на толщину диска
Таблица 2
Связь толщины диска ротора с параметрами модели и погрешностью срабатывания прибора
|
Деталь |
Конструктивный параметр |
Параметры детали |
Параметры модели |
Погрешность срабатывания |
||
|
Масса |
При наименьшем возможном значении параметра |
При наибольшем возможном значении параметра |
При наименьшем возможном значении параметра |
При наибольшем возможном значении параметра |
||
|
Ротор |
Допуск – 0,06 мм на толщину диска 0,9…0,84 мм |
4,8…4,6 гр |
Момент инерции ротора 0,343 (кг⋅мм2) Приведенный момент инерции Jпр = 110·10–5 кг·м2 КТ = 2,042∙10–5 Н⋅м⋅с⋅рад–1 |
Момент инерции ротора 0,351 (кг⋅мм2) Приведенный момент инерции Jпр = 113∙10–5 кг⋅м2 КТ = 2,19∙10–5 Н⋅м⋅с⋅рад–1 |
2 % |
0 % |
Согласно табл. 2, изменение толщины диска приводит к изменению погрешности срабатывания на величину в два процента.
Выводы
1. Полученная математическая модель интегрирующего акселерометра позволяет оценить влияние конструктивных параметров прибора на погрешность срабатывания.
2. Критичными конструктивными параметрами, существенно влияющими на настройку интегрирующего акселерометра, являются напряженность магнитного поля в рабочих зазорах первого и третьего регулирующего устройств, а также коэффициент торможения магнитного тормоза.
Заключение
В дальнейшем предполагается рассмотреть влияние технологического процесса на критичные конструктивные параметры. Предполагается проанализировать возможность оптимизации процессов сборки и настройки прибора с использованием разработанных математических моделей.
Рецензенты:Чечулин Ю.Б., д.т.н., профессор кафедры детали машин Института фундаментального образования Уральского федерального университета имени первого Президента России Б.Н. Ельцина, г. Екатеринбург;
Паршин В.С., д.т.н., профессор, заведующий кафедрой «Металлургические и роторные машины» Механико-машиностроительного института Уральского федерального университета имени первого Президента России Б.Н. Ельцина, г. Екатеринбург.
Работа поступила в редакцию 14.10.2013.
Библиографическая ссылка
Денисов Ю.В., Капленко М.В. КРИТИЧНЫЕ КОНСТРУКТИВНЫЕ ПАРАМЕТРЫ МИНИАТЮРНЫХ ИНТЕГРАЛЬНЫХ АКСЕЛЕРОМЕТРОВ // Фундаментальные исследования. – 2013. – № 10-8. – С. 1689-1693;URL: https://fundamental-research.ru/ru/article/view?id=32644 (дата обращения: 24.04.2024).