Преимущества электрических машин с полным бесконтактным магнитным подвесом ротора позволяют использовать их в тех областях, в которых применение машин с традиционными опорами невозможно из-за наличия смазки и механического контакта между вращающимися и неподвижными частями механизма. В конструкции такой машины, как минимум, должны присутствовать два модуля, удерживающих ротор в радиальном направлении, и один – в осевом. В настоящее время всё большее внимание уделяется электрическим машинам, совмещающим в одном модуле функции активного магнитного подшипника (АМП) и двигателя. Связано это с более выгодными массогабаритными показателями таких машин [3] и более эффективным использованием электроэнергии по сравнению с машинами на АМП.
Общий принцип построения бесподшипниковых электрических машин (БЭМ), в которых ротор приводится в движение вращающимся магнитным полем, был описан в 1973 году [5]. Согласно ему БЭМ должна иметь две трехфазные обмотки, числа пар полюсов которых различаются на один. Одним из примеров таких машин является синхронная индукторная бесподшипниковая машина (СИБМ). Математическая модель СИБМ, используемая зарубежными исследователями для построения системы управления, была описана в [4]. К недостаткам данной модели можно отнести отсутствие аналитических зависимостей между индуктивностями обмоток машины и её конструктивными параметрами, необходимыми для создания методики проектирования.
Конструкция модуля СИБМ
Модуль СИБМ во многом похож на обычную синхронную индукторную машину, имеющую трехфазную обмотку статора и явнополюсный ротор, число полюсов которого равно числу полюсов обмотки. В бесподшипниковом модуле в пазы статора дополнительно укладывается ещё одна трехфазная обмотка, число пар полюсов которой отличается на один.
Ротор модуля имеет четыре полюса, как и одна из обмоток статора (будем называть её обмоткой привода). Вторая обмотка (обмотка подвеса) – двухполюсная. Оси одноименных фаз обмоток привода и подвеса совпадают. Объём, занимаемый обмотками в пазах, определяется требуемым соотношением радиальной силы и момента модуля. Ширина полюса ротора составляет половину полюсного деления, т.к. при этом модуль имеет максимальный к.п.д. привода.
Преимущества СИБМ, по сравнению с другими типами БЭМ, связаны с отсутствием обмоток и постоянных магнитов на роторе: простота конструкции, низкая стоимость, сравнительно простой алгоритм управления, температурная независимость.
Математическая модель модуля СИБМ
Динамика ротора машины с полным бесконтактным магнитным подвесом уже была описана в [2]. Поэтому целью построения математической модели СИБМ является отыскание аналитических зависимостей радиальных сил и момента модуля от токов обмоток статора.
При построении математической модели были приняты следующие допущения:
– учитывается только первая гармоника магнитодвижущей силы (МДС) в зазоре;
– сталь сердечников статора и ротора не насыщена, и её магнитная проницаемость равна бесконечности;
– радиальные перемещения ротора малы по сравнению с величиной воздушного зазора;
– магнитная проводимость воздушного зазора между полюсами ротора близка нулю;
– потери на вихревые токи и перемагничивание малы.
Радиальные силы и момент определяются как производные магнитной энергии по соответствующей координате. Для упрощения выражений магнитная энергия записывается для машины с двухфазными обмотками привода и подвеса: 2a и 2b – фазы обмотки подвеса, 4а и 4b – фазы обмотки привода.
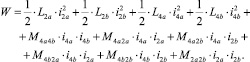 (1)
(1)
При определении собственных и взаимных индуктивностей использовались следующие обозначения (см. рис. 1): х, у – смещения ротора из центрального положения вдоль соответствующих осей; ϕ – угловая координата; ϕ – угол поворота ротора, отсчитываемый от горизонтальной оси х против часовой стрелки до центра одного из полюсов ротора; α – ширина полюса ротора в радианах.
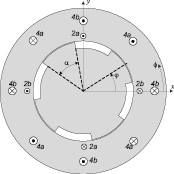
Рис. 1. Упрощенная модель СИБМ
Зависимость величины воздушного зазора от угловой координаты ϕ с учетом радиальных перемещений ротора описывается следующим выражением [1].
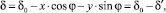 (2)
(2)
где δ0 – величина воздушного зазора при центральном положении ротора.
Для определения аналитических зависимостей индуктивностей обмоток статора от радиальных перемещений ротора приходится использовать приближенное выражение для обратной величины зазора машины. Связано это с тем, что результат интегрирования при нахождении этих выражений по точной формуле неудобен для использования.
Точное выражение для обратной величины зазора в зависимости от смещений и угловой координаты выглядит следующим образом.
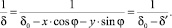 (3)
(3)
Приближенные выражения для обратной величины зазора представим степенным рядом.
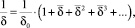 (4)
(4)
где 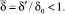 .
.
Так как величина воздушного зазора изменяется вдоль координаты ϕ, индуктивности обмоток надо определять как сумму индуктивностей бесконечно малых элементов dϕ. С учетом в (4) слагаемых второго порядка малости магнитная проводимость элемента зазора в точке с координатой φ:
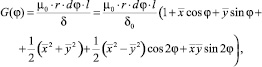 (5)
(5)
где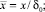
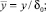 μ0 – магнитная проницаемость вакуума; r – радиус ротора; l – длина активной части сердечника
μ0 – магнитная проницаемость вакуума; r – радиус ротора; l – длина активной части сердечника
Поток обмотки элемента с координатой ϕ:
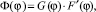 (6)
(6)
где F′(ϕ) – падение МДС на магнитном сопротивлении зазора в элементе с координатой ϕ.
При центральном положении ротора падение МДС на магнитном сопротивлении в каждом элементе зазора составляет половину полной МДС обмотки. Если ротор смещен, распределение МДС изменяется. Это изменение учитывается с помощью магнитного потенциала ротора f:
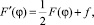 (7)
(7)
где 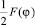 – распределение МДС обмотки в зазоре.
– распределение МДС обмотки в зазоре.
Магнитный потенциал определяется из первого закона Кирхгофа для магнитной цепи:
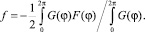 (8)
(8)
Часть собственной индуктивности обмотки, определяемая элементом зазора dϕ, может быть найдена следующим образом
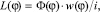 (9)
(9)
где Φ(φ) – поток обмотки через соответствующий элемент зазора; w(φ) – число витков обмотки, пересекаемых потоком Φ(φ); i – ток обмотки. Число витков обмотки, охватывающих элемент с координатой ϕ, определяется через распределение МДС. Т.к. учитывается только первая гармоника МДС, число витков обмотки:
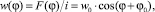 (10)
(10)
где w0 – полное число витков обмотки; φ0 – угол между осью обмотки и осью х.
Аналогично для взаимной индуктивности:
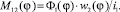 (11)
(11)
Пределы интегрирования при определении полной индуктивности обмотки являются координатами крайних точек полюсов ротора, т.к. проводимость воздушного зазора между полюсами не учитывается. В этом случае полная индуктивность:
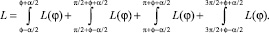 (12)
(12)
По выражениям (5)–(12) были определены собственные и взаимные индуктивности обмоток статора.
Полученные в результате дифференцирования магнитной энергии (1), выражения для момента M и радиальных сил Fx и Fyбыли упрощены с удержанием слагаемых первого порядка малости.
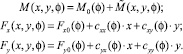 (13)
(13)
В выражениях (13) можно выделить полезные составляющие сил и момента (не зависящие от перемещений ротора) и возмущающие. С целью проверки точности расчета радиальных сил и момента по полученным уравнениям проведено моделирование модуля СИБМ методом конечных элементов (МКЭ).
Результаты расчета модели
При моделировании машины методом конечных элементов использовался программный пакет FEMM, позволяющий решать двумерные задачи по расчету электромагнитных полей. В модели использовались параметры статора асинхронного двигателя 4А71В4, на основе которого создается макет модуля СИБМ. В каждом пазу статора находится 50 витков обмотки привода и 35 витков обмотки подвеса.
Радиальные силы и вращающий момент являются, прежде всего, функциями тока обмоток привода и подвеса. В аналитическом расчете использовались значения токов, полученные из токов трёхфазных обмоток модели FEMM с помощью преобразования Кларка, при условии равенства создаваемой ими МДС. Характеристики получены для центрального положения ротора и угла поворота, равного π/8 радиан. На рис. 2, а показаны результаты расчета силы, действующей вдоль оси х, в зависимости от тока обмотки подвеса.
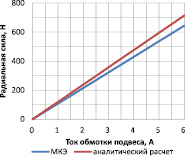
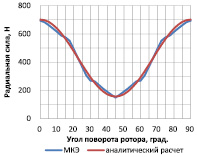
Рис. 2. Графики зависимости радиальной силы: а – от тока обмоток подвеса; б – от угла поворота ротора
Погрешность расчета радиальной силы связана со снижением магнитной проводимости зазора из-за наличия пазов статора. Так как электромагнитная сила прямо пропорциональна площади внутренней поверхности, эту разницу можно учесть простым введением коэффициента, не усложняя математическую модель. Кроме этого, результаты аналитического расчета оказываются заниженными, так как в математической модели не учтены боковые проводимости полюсов ротора. Дополнительная проводимость увеличивает силу также прямо пропорционально. Качественный расчет магнитной проводимости воздушного зазора при центральном положении ротора показал, что она отличается от проводимости, рассчитанной без учета боковых поверхностей полюсов и шлицев пазов статора, на 10 %. Погрешность расчета момента не превышает 5,2 % во всех точках измерения.
На рис. 2, б показаны результаты расчета радиальной силы при изменении угла поворота ротора. Расчет силы по аналитической зависимости проводился с учетом магнитной проводимости боковых поверхностей полюсов ротора и шлицев пазов статора. На графике видны колебания силы, рассчитанной методом конечных элементов, относительно аналитического расчета. Это связано с тем, что сила изменяется менее интенсивно, когда крайние точки полюсов ротора проходят под пазом статора. Изменение силы на других участках графика определяется величиной МДС под зубцами, которые в этот момент находятся над краями полюсов ротора. Погрешность вычисления силы по аналитической модели не превышает 10 % во всех точках измерения.
При центральном положении ротора ни одна из обмоток в отдельности не создает радиального усилия. На рис. 3 показаны результаты расчета радиальной силы, создаваемой обмоткой привода, при смещении ротора.
Из графика видно, что при смещении ротора более чем на 40 % от величины зазора при центральном положении возникает существенная погрешность. Это связано с тем, что в математической модели используется приближенное выражение для обратной величины зазора, верное лишь при малых смещениях.
Заключение
Полученные аналитические зависимости индуктивностей обмоток от конструктивных параметров позволяют рассчитать электромагнитные силы и момент проектируемой машины. Математическая модель обладает достаточной точностью для использования её в системе управления СИБМ. Учет нелинейности радиальной силы при больших смещениях вызовет существенное усложнение модели, что относится не только к бесподшипниковым машинам, но и к обычным АМП. Исследовать работу системы управления в подобных аварийных ситуациях надо на модели, повторяющей все свойства реального модуля, влияющие на его работу. На данный момент создаётся программная модель модуля СИБМ для использования в MATLABSimulink. Главными достоинствами данной модели является высокая точность расчета электромагнитных усилий и возможность расчета величины воздушного зазора по любому выражению (точному или приближенному).
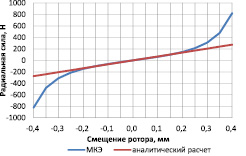
Рис. 3. График зависимости радиальной силы от смещения ротора
Рецензенты:
Баринов Ю.Г., д.т.н., профессор, ФГБОУ ВПО «Псковский государственный университет», г. Псков;
Плохов И.В., д.т.н., профессор, ФГБОУ ВПО «Псковский государственный университет», г. Псков.
Работа поступила в редакцию 17.10.2013.
Библиографическая ссылка
Домрачева Ю.В., Журавлев Ю.Н. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ МОДУЛЯ СИНХРОННОЙ ИНДУКТОРНОЙ БЕСПОДШИПНИКОВОЙ МАШИНЫ // Фундаментальные исследования. 2013. № 10-9. С. 1917-1921;URL: https://fundamental-research.ru/ru/article/view?id=32558 (дата обращения: 07.03.2026).



