Операция деления является одной из наиболее сложных арифметических операций. Её выполнение требует значительных временных затрат. Наиболее распространенные устройства деления представляют собой гетерогенные вычислительные структуры, реализующие различные итерационные способы, например, вычисление с ускорением на базе способа SRT. Подобные технические решения сложны для масштабирования и не обеспечивают высокой технологичности их производства при изменении форматов представления чисел.
Этих недостатков лишены спецпроцессоры (СП) на базе однородных вычислительных сред (ОВС) [1]. В таких средах однотипные базовые элементы (БЭ) соединены регулярными связями. Причем с введением в БЭ триггеров становится возможным организовать конвейерный режим работы ОВС, что в конечном счете ведет к повышению быстродействия. Таким образом, актуальна разработка новых способов МС для реализации данной операции на базе ОВС в параллельно-конвейерном режиме.
1. Способ итерационного деления SRT
В соответствии с алгоритмом SRT количество операций суммирования или вычитаний равно n/2,67 при делении двух n-разрядных чисел, что доказано статистически [5].
Схема на базе алгоритма SRT содержит сдвиговый регистр множителя, регистры множимого, удвоенного множимого и суммы частичных произведений, n-разрядный сумматор с распространением переноса, управляемый инвертор. Временная сложность QSRT устройства на базе SRT определяется произведением времени такта устройства TSRT на количество суммирований, то есть
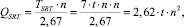
причем время такта равно произведению количества одноразрядных полных сумматоров n на количество логических элементов в наиболее длинной цепи распространения сигнала в каждом (семь элементов «И-НЕ») и на время срабатывания логического элемента t.
Аппаратная сложность RSRT данного устройства определяется произведением количества одноразрядных полных сумматоров n на количество логических элементов в каждом из них (15 элементов «И-НЕ»), а также количеством элементов памяти (каждый по четыре элемента «И-НЕ») в четырех n-разрядных регистрах и n-разрядным управляемым инвертором, то есть
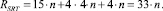
Тогда удельная производительность GSRT одного логического элемента составит
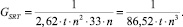
Полученное выражение временной сложности устройства на базе SRT показывает квадратичную зависимость от разрядности сомножителей. Аппаратная сложность увеличивается прямо пропорционально количеству сомножителей и их разрядности. Удельная производительность обратно пропорциональна кубу от разрядности чисел.
2. Способ деления целых двоичных чисел без остатка, начиная с младших разрядов
Способ алгебраического деления модулей чисел, представленных в позиционной системе счисления, на базе операции МС с пирамидальным выделением переносов (ПВП) [3] заключается в следующем (способ ДМС) [2].
1. Производится запись разрядов делителя в ячейки первой строки двумерной матрицы A размерностью n строк и n столбцов на элементах памяти. В ячейки каждой последующей строки записывается делитель, сдвигаемый на один разряд в сторону старших при переходе к следующей строке, освободившиеся разряды заполняются нулями. Столбцы матрицы являются соответствующими разрядными срезами SRn, …, SR2, SR1.
2. Первый разряд s1 искомого частного S становится равным сумме по модулю два младшего разряда SR1 и первого разряда делимого, в остальные разряды n-разрядного частного записываются нули.
3. Производится поразрядное логическое умножение разрядов SR2 на соответствующие разряды частного, результирующий вектор D2 = SR2∙S.
4. Выполняется операция пирамидального выделения переносов вектора D2. В результате формируется вектор переносов С2 и одноразрядный вектор B2.
5. Второй разряд s2 частного S становится равным сумме по модулю два вектора B2 и второго разряда делимого.
6. Производится поразрядное логическое умножение разрядов SR3 на соответствующие разряды частного, результирующий вектор D3 = SR3∙S.
7. Выполняется операция пирамидального выделения переносов вектора D3 с учетом вектора переносов С2. В результате формируется вектор переносов С3 и одноразрядный вектор B3.
8. Третий разряд s3 частного S становится равным сумме по модулю два вектора B3 и третьего разряда делимого.
9. Далее процесс вычисления последующих разрядов частного S(sn, …, s2, s1) аналогичен п.п. 6–8 до момента вычисления значения разряда sn.
10. После определения значения разряда sn полученное значение S(sn, …, s2, s1) есть значение искомого частного в n-разрядной машинной сетке.
Пример. Требуется разделить два четырехразрядных числа (n = 4):
делимое a1 = 1111;
делитель a2 = 0101.
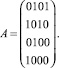
Битовая матрица A сдвигаемого в сторону старших разрядов делителя имеет четыре разрядных среза: SR1 = 0001, SR2 = 0010, SR3 = 0101, SR4 = 1010. Первый разряд частного  становится равным инверсии суммы по модулю два младшего разряда SR1 и первого разряда делимого, остальные разряды частного становятся равными нулю S = 0001. Вычисляется D2 = SR2∙S = 0010∙0001 = 0000. Выполняется операция пирамидального выделения переносов, в результате С2 = 000, B2 = 0. Второй разряд s2 = 0⊕1 = 1. В итоге серии аналогичных вычислений будет получено искомое частное S(s4, s3, s2, s1) = 0011.
становится равным инверсии суммы по модулю два младшего разряда SR1 и первого разряда делимого, остальные разряды частного становятся равными нулю S = 0001. Вычисляется D2 = SR2∙S = 0010∙0001 = 0000. Выполняется операция пирамидального выделения переносов, в результате С2 = 000, B2 = 0. Второй разряд s2 = 0⊕1 = 1. В итоге серии аналогичных вычислений будет получено искомое частное S(s4, s3, s2, s1) = 0011.
3. Спецпроцессор деления целых двоичных чисел без остатка
Вычислительное ядро СБИС-процессора для выполнения алгебраического деления состоит из устройства умножения n-разрядных двоичных чисел на базе МС [4] и блока управления синхронизацией. При этом входы МС Qp – Q1 являются отдельными входами синхронизации триггеров канала переноса соответствующих столбцов ОВС мультиоперандного сумматора, где p = log2n – количество столбцов МС. Вход Qp + 1 является входом синхронизации блока формирователя разрядных срезов, входящего в состав устройства умножения. Блок управления синхронизацией, в общем виде организация которого представлена на рис. 1, состоит из 2∙p информационных D-триггеров, p + 1 элементов И, элемента ИЛИ, входа синхронизации c, инверсного входа сброса r, управляющего одноразрядного входа D, одноразрядных выходов Qp+1 – Q1.
Блок управления синхронизацией обеспечивает первое прохождение каждого разрядного среза через МС без изменения состояния каналов переноса, что позволяет сформировать разряд частного, соответствующий разрядному срезу, который при повторном прохождении этого же разрядного среза участвует в формировании единиц переноса.
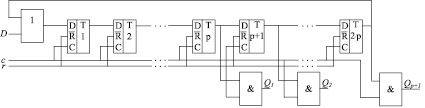
Рис. 1. Организация блока управления синхронизацией
Для выполнения операции деление нацело к устройству умножения, выполненному на базе мультиоперандного сумматора, добавлен блок управления синхронизацией и элемент «ИСКЛЮЧАЮЩЕЕ ИЛИ». Организация вычислительного ядра представлена на рис. 2, где D – одноразрядный управляющий вход, X – одноразрядный вход подачи делимого, Y – одноразрядный вход подачи делителя, S – одноразрядный информационный выход, с и r – входы синхронизации и сброса соответственно.
Перед началом операции деление на управляющий вход устройства D в течение одного такта подается значение логической единицы. В последующие такты на управляющий вход устройства D подается значение логического нуля. На вход Y последовательно подаются значения разрядов делителя. На выход X последовательно подаются значения разрядов делимого, начиная с младших, каждый log2n + 1 такт.
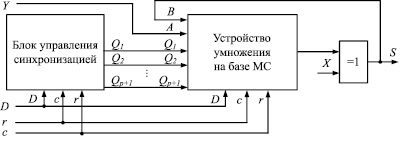
Рис. 2. Организация вычислительного ядра СБИС-процессора
Пример. Требуется разделить а1 на а2 (n = 2):
a1 = 11,
a2 = 01.
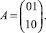
Битовая матрица A массива частичных произведений имеет два разрядных среза: SR1 = 01, SR2 = 10. Вычислительный процесс в ОВС приведен на рис. 3, где красным и синим цветом отмечено вычисление первого и второго разряда искомого частного соответственно. Размерность мультиоперандного сумматора на базе способа ПВП составляет одну ЯОС3, так как log22 = 1. Исходные операнды подаются на информационные входы ОВС X и Y последовательно, начиная с младшего разряда каждый такт синхронизации.
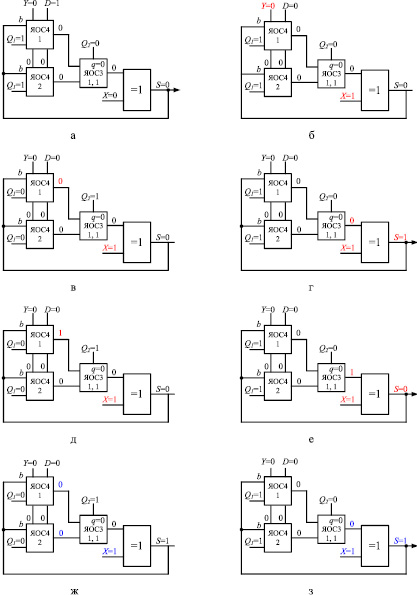
Рис. 3. Пример выполнения операции умножение: (а)–(з) процесс формирования результата
Разряды искомого результата доступны на выходе S спустя 1 + log22 = 2 такта работы устройства после подачи младшего разряда исходных чисел. Таким образом, результаты расчета формируются в форме векторов на выходе S за восемь тактов работы устройства.
4. Сопоставление оценок эффективности способов деления
Для вычисления частного от деления n-разрядных чисел устройству необходимо выполнить одно мультиоперандное суммирование разрядных срезов, однако вычисления над каждым разрядным срезом выполняются с задержкой в log2n тактов, то есть
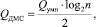
причем при устройстве умножения на базе ПВП [4] временная сложность составит
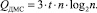
Аппаратная сложность Rдел устройства деления суммой аппаратных затрат блока управления синхронизацией и устройства умножения, то есть
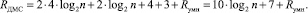
При использовании устройства МС на базе пирамидального выделения переносов аппаратная сложность составит
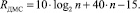
Тогда удельная производительность GДМС одного логического элемента при использовании устройства суммирования на базе пирамидального выделения переносов составит
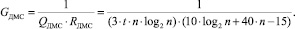
В таблице приведены результаты расчета характеристик устройств деления на базе способов SRT и ДМС.
Таким образом, полученное выражение временной сложности устройства деления на базе устройства суммирования с пирамидальным выделением переносов показывает возрастание временной сложности по сравнению с умножением на базе этого же способа суммирования в log2n раз. При этом аппаратная сложность увеличивается незначительно.
Результаты расчета характеристик
|
n, бит |
Временная сложность |
Аппаратная сложность |
Удельная производительность |
|||
|
SRT, нс |
ДМС, нс |
SRT, шт. |
ДМС, шт. |
SRT, оп/с |
ДМС, оп/с |
|
|
64 |
10732 |
2605 |
2112 |
2729 |
44,090 |
106,029 |
|
128 |
42926 |
5175 |
4224 |
5427 |
5,511 |
26,708 |
|
256 |
171704 |
10305 |
8448 |
10813 |
0,689 |
6,702 |
|
512 |
686817 |
20555 |
16896 |
21575 |
0,086 |
1,679 |
|
1024 |
2747269 |
41045 |
33792 |
43089 |
0,011 |
0,42 |
Временная сложность устройства деления на базе МС прямо пропорциональна разрядности сомножителей, тогда как для устройства на базе алгоритма SRT она возрастает квадратично. Наиболее выгодным с точки зрения временной сложности является устройство на базе МС. Например, при разрядности операндов n = 256 бит его временные затраты в 16 раз меньше, чем для устройства на базе SRT. Аппаратная сложность устройства на базе МС больше в 1,28 раза по сравнению с устройством на базе SRT. Удельная производительность устройств деления уменьшается с ростом разрядности. Наиболее выгодным с точки зрения удельной производительности является устройство на базе ДМС. Например, при разрядности сомножителей n = 256 бит, его удельная производительность в 38 раз выше, чем для устройства на базе SRT.
Заключение
Предложен способ деления двоичных положительных чисел нацело, отличающийся от известных тем, что деление производится с помощью операции мультиоперандного суммирования, начиная с младших разрядов делимого. Предложенный способ по сравнению с известным итерационным способом позволяет повысить скорость вычислений в n/log2n раз, где n – разрядность операндов.
Предложена организация вычислительной ячейки и на её базе организация конвейерной однородной вычислительной среды для формирования разрядных срезов делимого на основе способа деления с использованием операции мультиоперандного суммирования. В отличие от известных аналогов вычислительная среда после заполнения ]log2n[ ступеней конвейера Tконв = (]log2n[+1)∙tя обеспечивает выдачу результата деления за n∙tя/log2n, где tя – время срабатывания вычислительной ячейки, n – разрядность операндов.
Рецензенты:
Частиков А.В., д.т.н., профессор, декан факультета прикладной математики и телекоммуникаций Вятского государственного университета, г. Киров;
Шатров А.В., д.ф.-м.н., профессор, заведующий кафедрой математического моделирования в экономике Вятского государственного университета, г. Киров.
Работа поступила в редакцию 08.10.2013.
Библиографическая ссылка
Осинин И.П. СПОСОБ И УСТРОЙСТВО ДЛЯ ВЫПОЛНЕНИЯ ПАРАЛЛЕЛЬНО-КОНВЕЙЕРНЫХ ОПЕРАЦИЙ ДЕЛЕНИЯ НАЦЕЛО // Фундаментальные исследования. 2013. № 10-6. С. 1228-1233;URL: https://fundamental-research.ru/ru/article/view?id=32521 (дата обращения: 12.03.2026).



