Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Осинин И.П. 1

---

1 ФГБОУ ВПО «Вятский государственный университет»

Рассмотрен способ алгебраического суммирования М компонентных массивов n-разрядных двоичных чисел с фиксированной или плавающей точкой, отличающийся тем, что последовательная операция суммирования заменяется параллельно исполняемой операцией пирамидального выделения переносов. Предложенный способ по сравнению с известным итерационным способом позволяет повысить скорость вычислений в m раз. Предложена организация вычислительной ячейки и на её базе организация конвейерной однородной вычислительной среды для вычисления суммы m n-разрядных чисел на основе данного способа вычислений. В отличие от известных аналогов вычислительная среда обеспечивает параллельно-конвейерное вычисление суммы m n-разрядных чисел и после заполнения p ступеней конвейера Tконв = p∙tя обеспечивает выдачу результата суммирования за n∙tя, где p = ]log2m[, tя – время срабатывания вычислительной ячейки. Проведено сравнение полученных характеристик с известным структурами для решения подобных задач.

Статья в формате PDF

536 KB

мультиоперандный сумматор

однородная вычислительная среда

пирамидальное выделение переносов

параллельно-конвейерная операция

1. Каляев И.А., Левин И.И., Семерников Е.А. Реконфигурируемые мультиконвейерные вычислительные структуры. – Ростов-на-Дону: ЮНЦ РАН, 2008. – 393 с.

2. Осинин И.П., Князьков В.С. Способ организации вычислений суммы n m-разрядных чисел // Первый всероссийский конгресс молодых ученых: сез. докл. – СПб., 2012. – С. 87–88.

3. Осинин И.П., Князьков В.С. Способ организации вычислений суммы N М-разрядных чисел // Патент РФ № 2450327 от 10 мая 2012 г.

4. Осинин И.П., Князьков В.С., Волченская Т.В. Организация арифметического разрядно-параллельного СБИС-процессора для массовых вычислений // Высокопроизводительные параллельные вычисления на кластерных системах»: сборник материалов XII Всероссийская конференция. – Нижний Новгород: Изд-во Нижегородского госуниверситета, 2012. – С. 194–198.

5. Цилькер Б.Я., Орлов С.А. Организация ЭВМ и систем: учебник для вузов – СПб., 2004. – 667 с.

Операция мультиоперандного суммирования (МС), то есть суммирования m n-разрядных чисел, является достаточно распространенной арифметической операцией в вычислительной математике. Например, при перемножении матриц после умножения строки на столбец вычисляется сумма элементов, составляющих результат умножения. Однако на данный момент в универсальных процессорах операция МС не представлена на аппаратном уровне в виде отдельной команды, а выполняется итерационно с помощью двухоперандного суммирования, что приводит к значительному увеличению времени вычислений [2]. С другой стороны, известные алгоритмы МС ориентированы на построение гетерогенных структур, включающих блоки суммирования, регистров, логики управления и других. В настоящее время в вычислительной технике наиболее распространены устройства на базе итерационного способа с ускоренным переносом (ИСС), бинарного дерева (БД) и дерева Уоллеса (ДУ). Их подробное описание приведено в [5]. Технические решения, построенные на их базе, сложны для масштабирования и не обеспечивают высокой технологичности их производства при изменении форматов представления чисел.

Этих недостатков лишены спецпроцессоры (СП) на базе однородных вычислительных сред (ОВС). В таких средах однотипные базовые элементы (БЭ) соединены регулярными связями [1]. Причем с введением в БЭ триггеров становится возможным организовать конвейерный режим работы ОВС, что в конечном счете ведет к повышению быстродействия. Таким образом, актуальна разработка новых способов МС для реализации данной операции на базе ОВС в параллельно-конвейерном режиме.

1. Классический способ бинарного мультиоперандного суммирования

Известный способ МС на базе бинарного дерева (БД) заключается в следующем:

1. Суммируются пары слагаемых A1 и А2, А3 и А4,…, Аj и Aj+1,…, Am-1 и Am.

2. Полученные суммы S1,1, S1,2,…S1,j,…, S1,]m/2[ выступают в роли слагаемых, которые также суммируются парами, в результате вычисляются суммы S2,1, S2,2,…S2,j,…S2,]m/4[.

3. Вычисления продолжаются подобным образом, пока не будет вычислена искомая сумма Sp,1, где p = ]log2m[.

Временная сложность Qбд устройства на базе БД определяется произведением времени такта работы каскада устройства Tбд на логарифм от количества слагаемых по основанию два, округлённый до большего целого (количество ступеней), то есть

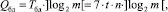
причем время работы каскада устройства равно произведению количества одноразрядных полных сумматоров n на количество логических элементов в наиболее длинной цепи распространения сигнала в каждом (7 элементов «И-НЕ») и на время срабатывания логического элемента t.

Аппаратная сложность Rбд данного устройства определяется произведением количества одноразрядных полных сумматоров n на количество логических элементов в каждом из них (15 элементов «И-НЕ»), а также количеством элементов памяти на D-триггерах (каждый по четыре элемента «И-НЕ») в m n-разрядных входных регистрах, то есть

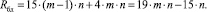
Тогда удельная производительность Gбд одного логического элемента составит

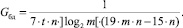
Полученное выражение временной сложности устройства на базе БД показывает логарифмическую зависимость от количества слагаемых и прямо пропорциональную зависимость от их разрядности. Аппаратная сложность увеличивается прямо пропорционально росту количества слагаемых и их разрядности. Удельная производительность обратно пропорциональна количеству слагаемых и квадрату их разрядности. Недостаток данного способа состоит в низком быстродействии, которое зависит как от количества слагаемых, так и от их разрядности.

2. Способ мультиоперандного суммирования

Операция пирамидального выделения переносов заключается в следующем [3]. В специализированной однородной вычислительной среде параллельно выполняется свертка редукционным суммированием соседних пар разрядов исходного m-разрядного вектора с учетом (m – 1)-разрядного вектора переносов С*. На каждом шаге свертки разрядность исходного вектора уменьшается вдвое. Таким образом, через p шагов свертки исходный вектор будет сжат в искомый одноразрядный вектор B и (m – 1)-разрядный вектор С переносов, где p = log2m.

Способ выполняются следующим образом (способ – ПВП).

1. Выполняется операция пирамидального выделения переносов в двоичном m-разрядном срезе SR1. В результате формируется вектор переносов С1 и одноразрядный вектор B1, который является первым разрядом s1 искомой суммы S массива M.

2. Выполняется операция пирамидального выделения переносов в m-разрядном срезе SR2 с учетом вектора переносов С1. В результате формируется вектор переносов С2 и вектор B2, который является вторым разрядом s2 искомой суммы S.

3. Выполняется операция пирамидального выделения переносов в m-разрядном срезе SR3 с учетом вектора переносов С2. В результате формируется вектор переносов С3 и вектор B3, который является третьим разрядом s3 искомой суммы S.

4. Далее процесс вычисления последующих разрядов суммы S(sp, …, sn+1, sn, …, s2, s1) аналогичен п.п. 2, 3 до момента вычисления значения разряда sn, где p = n + log2m.

5. После определения значения разряда sn могут возникнуть следующие ситуации.

Случай 1. При Cn = 0 полученное значение S(sn, …, s2, s1) есть значение искомой суммы в n-разрядной машинной сетке.

Случай 2. При Cn > 0, при вычислениях в n-разрядной машинной сетке возникла ситуация переполнения и значение S некорректно. Разрешение этой ситуации возможно следующими способами в случае, если разрядная сетка вычислительной среды рассчитана на наихудший случай и переполнений в ней не возникает:

Способ 1. Выполняется расчет по п. 6 значения p-разрядной суммы S(sp, …, sn+1, sn, …, s2, s1). Вывод модуля S из вычислительной среды выполняется последовательной передачей q n-разрядных блоков: (sn, …, s2, s1), (s2n, …, sn+2, sn+1), …, (sp, …, sn(q–1)+2, sn(q–1)+1).

Способ 2. Выполняется расчет по п.6 значения p-разрядной суммы S(sp, …, sn+1, sn, …, s2, s1). При исходном представлении массива чисел в формате с плавающей точкой и n-разрядном представлении мантисс несложными аппаратными средствами выполняется их нормализация с соответствующей коррекцией порядка.

6. Выполняется операция пирамидального выделения переносов в двоичном векторе Cn. В результате формируется вектор переносов Сn+1 и вектор Bn+1, который является разрядом sn+1 искомой суммы S. Далее процесс продолжается аналогичным образом до момента определения последнего разряда sm–1 итоговой суммы S.

Пример. Требуется вычислить сумму модулей четырех двоичных чисел:

a1 = 00110,

a2 = 00101,

a3 = 00111,

a4 = 00011.

Битовая матрица A массива этих чисел (2) имеет пять разрядных срезов: SR1 = 1110, SR2 = 1101, SR3 = 0111, SR4 = 0000, SR5 = 0000. Выполняется операция пирамидального выделения переносов в разрядном срезе SR1. В результате формируется вектор переносов С1 = 010 и одноразрядный вектор B1 = 1, который является первым разрядом s1 искомой суммы S. Затем выполняется операция пирамидального выделения переносов в разрядном срезе SR2 с учетом вектора переносов С1. В результате формируется вектор переносов С2 = 110 и одноразрядный вектор B2 = 0, который является вторым разрядом s2 искомой суммы S. В итоге серии аналогичных вычислений будет получена искомая сумма S(s5, s4, s3, s2, s1) = 10101.

3. Спецпроцессор на базе способа пирамидального выделения переносов

ОВС, организация которой представлена на рис. 1, состоит из ячеек однородной среды (далее ЯОС), информационных входов Xm – X1, информационного выхода Y, входа синхронизации с и инверсного входа сброса r, которые соединены с соответствующими входами каждой ячейки (для компактности представления на рисунке не изображены), где m – число слагаемых [4]. Мультиоперандный сумматор имеет древовидную структуру. В каждом следующем столбце в два раза меньше ячеек, чем в предыдущем, причем число столбцов p = ]log2m[.

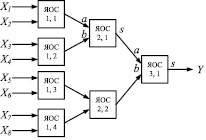
Рис. 1. Организация однородной вычислительной среды

В состав ЯОС входят: a, b – два одноразрядных информационных входа, c – вход синхронизации, r – инверсный вход сброса, s – одноразрядный информационный выход, q – канал переноса. ЯОС реализует следующую систему логических функций в базисе И-НЕ на триггерах Эрла:

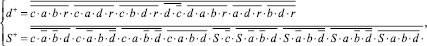
Общее число ячеек ОВС m-1. Каждый такт на вход c ячеек ОВС подается сигнал синхронизации. На входы Xm – X1 подаются разрядные срезы, причем каждый следующий должен быть подан разрядный срез. ОВС реализует операцию пирамидального выделения переносов над i-м разрядным срезом, в результате которой формируется i-й разряд искомой суммы, i∈[1; n]. Формируемые при этом единицы переносов посредством обратной связи в ячейке учитываются при обработке следующего разрядного среза. В результате через p = ]log2m[ тактов работы устройства на выходе Y формируется младший разряд искомой суммы. После этого конвейер является заполненным, и разряды суммы формируются на выходе Y каждый следующий такт.

Пример. Необходимо сложить четыре (m = 4) четырехразрядных (n = 5) операнда: a1 = 0101, a2 = 0001, a3 = 0011, a4 = 0110.

a1 = 0101,

a2 = 0001,

a3 = 0011,

a4 = 0110.

Битовая матрица A массива этих чисел имеет четыре разрядных среза: SR1 = 0111, SR2 = 1100, SR3 = 1001, SR4 = 0000. Тогда размерность однородного вычислительного ядра составит p = ]log2m[ = 2 столбца, причем в первом столбце ]log2m[ = 2 строки, во втором ]log2(m/2)[ = 1 строка. Вычислительный процесс в ОВС приведен на рис. 2, где красным и синим цветом отмечено вычисление первого и второго разряда искомой суммы соответственно.

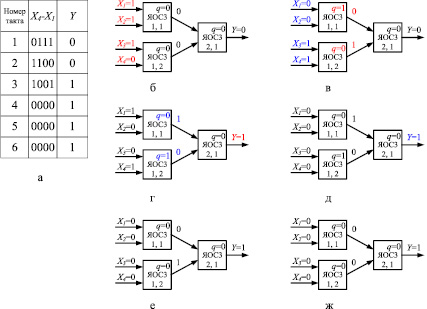
Рис. 2. Пример выполнения операции МС: а–ж – процесс выполнения операции

Искомая сумма S = (s4, s3, s2, s1) = 1111, причем её младший разряд доступен на выходе Y через два такта после подачи первого разрядного среза на вход устройства (число тактов заполнения конвейера p = 2).

4. Сопоставление оценок эффективности способов мультиоперандного суммирования

Временная сложность операции МС Qпвп в данном спецпроцессоре в конвейерном режиме после заполнения ]log2m[ ступеней конвейера линейно зависит от разрядности слагаемых и составляет n тактов, то есть

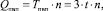
где n – разрядность слагаемых, m – их количество. Причем время такта определяется количеством логических элементов в наиболее длинной цепи распространения сигнала ЯОС3 (три элемента И-НЕ при реализации на базе триггера Эрла с логикой) и временем срабатывания t каждого из них.

Аппаратная сложность спецпроцессора Rпвп определяется произведением числа ЯОС3 m – 1 на число логических элементов в каждом из них (22 элемента И-НЕ), то есть

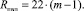
Тогда удельная производительность Gпвп каждого логического элемента составит

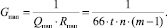
Таким образом, временная сложность прямо пропорциональна разрядности слагаемых и не зависит от их числа. Аппаратная сложность прямо пропорциональна числу слагаемых и не зависит от их разрядности. Удельная производительность обратно пропорциональна разрядности слагаемых и их числу.

В таблице приведены результаты расчета временной сложности устройств для МС на базе способов БД и ПВП.

Результаты расчета характеристик

Тогда временная сложность устройств мультиоперандного суммирования прямо пропорциональна разрядности слагаемых, однако для устройства на базе ПВП она является наименьшей. Временная сложность устройства на базе предложенного способа не зависит от количества слагаемых. Аппаратная сложность рассматриваемых устройств пропорциональна количеству слагаемых. Для устройств на базе ПВП она является наименьшей.

Заключение

В работе рассмотрен способ мультиоперандного суммирования, отличающийся тем, что последовательная операция суммирования заменена параллельно-конвейерным пирамидальным выделением переносов в разрядных срезах. Предложенный способ по сравнению с известным способом БД позволяет повысить скорость вычислений в log2m раз.

Предложена организация вычислительной ячейки и на её базе организация конвейерной однородной вычислительной среды для вычисления суммы m n-разрядных чисел с фиксированной и плавающей точкой на основе способа вычислений с использованием операции пирамидального выделения переносов в двоичных векторах. В отличие от известных аналогов вычислительная среда обеспечивает вычисление суммы m n-разрядных чисел и после заполнения ]log2m[ ступеней конвейера Tконв = ]log2m[∙tя обеспечивает выдачу результата суммирования за n∙tя, где tя – время срабатывания вычислительной ячейки. В результате оценки эффективности предложенного устройства в сравнении с аналогами установлено, что использование однородных вычислительных сред, сконструированных на базе предложенного способа суммирования, обеспечивает повышение скорости вычислений. Например, для 64-х слагаемых с разрядностью 64 бита вычисления будут выполняться в 14 раз быстрее, чем в устройстве на базе бинарного дерева при сокращении аппаратной сложности в 17 раз.

Рецензенты:

Частиков А.В., д.т.н., профессор, декан факультета прикладной математики и телекоммуникаций Вятского государственного университета, г. Киров;

Шатров А.В., д.ф.-м.н., профессор, заведующий кафедрой математического моделирования в экономике Вятского государственного университета, г. Киров.

Работа поступила в редакцию 23.09.2013.

Библиографическая ссылка