При взаимодействии биологического объекта (клетка, организм, популяция) неизбежно возникает биотехническая система (БТС) с превалированием определенных технических компонент физического, химического или механического характеров. Причем при временно-пространственном согласовании и совместной работе биологической и технической составляющих БТС возникают различные функциональные состояния (ФС) как отдельных элементов так и системы в целом.
Между функционированиями технической и биологической частей неизбежно возникают «противоречия»: - по целям функционирования: в технической части - оптимальность, в биологической - предпочтительность; - по времени реакции на воздействие: в технических элементах на несколько порядков быстрее; - по «времени жизни» и «усталости» элементов; - по способам «декомпенсации» негативных изменений.
Из этих противоречий возникают проблемы: количественной оценки напряженностей ФС подсистем; согласования во времени напряженностей ФС подсистем; своевременная и качественная коррекция ФС подсистем.
Таким образом, можно предложить, учитывая в основном колебательное доминирование динамики напряженности биологической части БТС, использовать технические элементы, работающие синхронно с биологической, но в «противофазе» или компенсируя повышение напряженности первой. (Кстати, это же касается и «подстройки» биологической части к технической). В этом случае, напряженность функционального состояния БТС будет выглядеть примерно так.
Отметим так же, что при взаимодействии биологической и технической частей могут наступить и «резонансные» явления действующие как деструктивно, так и позитивно (достижение хорошего эффекта при минимальных затратах и управляющих воздействиях).
Таким образом, мы подошли к вопросу оценки уровня напряженности функционального состояния. По отношению к биологическим объектам, эту проблему на качественном уровне решалась, в частности, Анохиным П.К., Судаковым К.В. Они предлагают пять уровней напряженности функционального состояния и дают качественную характеристику этих состояний (заметим, на первом этапе решения данной проблемы учеными предлагалось выделять три состояния: не напряженное, напряженное и промежуточное.) Например, представленные в Таблице 1.
Таблица 1. Уровни напряженности функционального состояния
|
№ уровня состояния функциональной системы |
Характеристика уровня функционального состояния |
функционирование организма |
Доминирование обратных связей |
|
1. Состояние нормы |
Отсутствие сдвигов функционального состояния. Высокостабильные взаимоотношения функций системы. Нормальный уровень напряжения регуляторных механизмов межсистемной интеграции. |
Гомеостаз |
Отрицательные |
|
2. Группа риска |
Незначительные изменения функционального состояния. Незначительное повышение уровня напряженности регуляторных механизмов межсистемной интеграции. |
Самоорганизация |
Отрицательные |
|
3. Состояние 1 степени напряженности |
Умеренное повышение уровня напряжения и рассогласования регуляторных механизмов межсистемной интеграции. |
Самовосстановление, малые флуктуации («рыскание») |
Неустойчивая «точка баланса» отрицательных и положительных |
|
4. Состояние 2 степени напряженности |
Выраженные изменения функционального состояния, напряжения и рассогласования регуляторных механизмов межсистемной интеграции. |
Переход в новое состояние с возможностями восстановления, бифуркации, большие флуктуации |
Положительные |
|
5. Состояние 3 степени напряженности |
Резко выраженные изменения функционального состояния. Высокий уровень напряжения и рассогласования регуляторных механизмов межсистемной интеграции. |
Переход в новое состояние без самовозможности восстановления, бифуркации практически отсутствуют, флуктуаций нет |
Отрицательные - «закрепляющие» новые состояния |
(Заметим, что поскольку развитие патологического процесса можно рассматривать как последовательное «прохождение» организма из одного устойчивого состояния в другое, то это характеризуется последовательной сменой функциональных состояний, а значит использоваться в лечебно-диагностическом процессе - исследовательские работы в этом направлении были начаты в Курском государственным медицинском университете школой Завьялова А.В. и успешно продолжаются в настоящее время.)
Для того, что бы управлять уровнем напряженности ФС со стороны технической части (механически, химически или физически, психологически и т.п. способами), необходимо количественная оценка уровня напряженности. В частности, школой Завьялова А.В. был разработан для этой цели так называемый «Показатель системной организации функциональных систем» - ПСОФС. При исследовании динамики развития ряда заболеваний были получены интересные результаты, позволяющие на этапе скрининга или телемедицины производить первичную диагностики. При этом было замечено, например в работах Дроновой Т.А., что при развитии заболеваний печени, ПСОФ, вычисленный по результатам общего или биохимического анализа крови, по мере развития гепатита последовательно увеличивался, а затем уменьшался при циррозе. Здесь нет никакого противоречия, поскольку при циррозе организм уже «не сопротивляется», он перешел в новое состояние и, следовательно, его функциональное напряжение не велико.
Рассмотрим на ряд формул, применяемых для решения классификационных задач в теории распознавания образов.
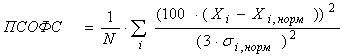 (1)
(1)
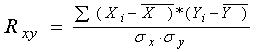 (2)
(2)
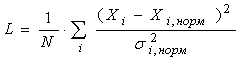 (3)
(3)
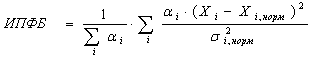 (4)
(4)
Формула (1) применяется школой Завьялова А.В., формула (2)- классический коэффициент парной корреляции, формула (3) - нормированный по дисперсии некого «начального» состояния квадрат расстояния анализируемого объекта в пространстве состояний (используется в теории распознавания образов), формула (4) - предлагаемый нами «интегральный показатель функционирования биообъекта», который учитывает весовую нагрузку (информационную значимость) каждого признака.
Хорошо видно «смысловое подобие» данных формул - количественная характеристика корреляции (близости), - поэтому эти формулы могут быть использованы для количественной оценки напряженности функционального состояния систем, характеризующими вектором дискретных значений некоторых характеристик. В качестве нормативных значений характеристик могут быть использованы: среднее или модальное значение величины в норме (в том числе, индивидуальной или рекомендуемой) или значению «нормативного аттрактора».
В случае применения аналогового одномодального сигнала-характеристики (например, ЭКГ) формула (4) принимает вид - (5):
![]() (5),
(5),
где Xa(t) - аттрактор или эталон нормативного состояния (поведения).
Поскольку, как показали практические исследования, применение формул (1) или (4) имеют большие величины, то нами предлагается перейти к логарифмической шкале, а именно, в качестве количественной меры напряженности использовать подобные теории связи следующий логарифмический показатель:
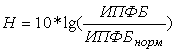 (6).
(6).
Единицей измерения тогда можно принять - Дб (децибел).
К особенностям формулы (6) следует отнести следующее: во-первых, в случае если в качестве Х при вычислении ИПФБ использовались нормированные по математическому ожиданию и дисперсии базового класса величины ![]() и формула (6) принимает вид:
и формула (6) принимает вид: ![]() , во-вторых, если в качестве
, во-вторых, если в качестве ![]() использовать в (6) значение показателя ИПФБ, вычисленное в «соседнем классе» функционального состояния, то (6) можно использовать для оценки «крутизны перехода», т.е построить и проанализировать своеобразную логарифмическую амплитудную характеристику функционирования организма (или развития патологического процесса).
использовать в (6) значение показателя ИПФБ, вычисленное в «соседнем классе» функционального состояния, то (6) можно использовать для оценки «крутизны перехода», т.е построить и проанализировать своеобразную логарифмическую амплитудную характеристику функционирования организма (или развития патологического процесса).
Все вышесказанное относится и к технической части БТС. Более того, поскольку в (6) применяется относительная величина, то появляется возможность соизмерять, а значит использовать для управления, напряженностей ФС биологической и технической составляющих в БТС.
Таким образом, мы определись с количественной оценкой напряженности функционального состояния.
Остановимся еще на одном вопросе: что считать «нормативным» классом?
Ответ на этот вопрос, безусловно, вытекает из целей исследования, например:
- если необходимо проанализировать напряженность работы определенной функциональной подсистемы в эргатической системе или развитии патологического процесса, то рекомендуется использовать среднестатистическую (а, если есть возможность, индивидуальную) норму;
- если речь идет о дифференциальной диагностике («сломан» - «не сломан», «наблюдается» определенное заболевание - «не наблюдается» и т.п.), то рекомендуется применять значения характеристик при «болезни»;
- если речь идет о химических реакциях, то здесь лучше «идеального» опыта, согласно таблице Менделеева Д.И. пожалуй вряд ли что будет;
- если осуществляется анализ экологического давления на население, то рекомендуется использовать ПДК веществ;
- если необходимо проанализировать социально-психологический или экономический статусы населения (популяции), то в качестве нормы очевидно необходимо выбирать желаемое (предпочтительное) состояние;
- и т.п., - главное при выборе отвечать на вопросы «зачем?» и «каким образом корректировать?», т.е.: «целевая функция» и «акцептор действия».
Применение рассмотренного показателя оценки уровня напряженности функционального состояния (НФС) для построения решающих правил идентификации классов состояний предполагает следующую методологию.
На первом этапе осуществляется сбор фактологического репрезентативного материала и отбрасываются артефакты. Общая выборка случайным образом делится на три части - обучающую, настраивающую и экзаменационную. На перовой выборке рассчитывается напряженность. На второй - определяются функции принадлежности. На третьей выборке определяется эффективность идентифицированных диагностических решающих правил. Соотношения статистических мощностей указанных выборок рекомендуется выбирать исходя из взаимной репрезентативности (они должны подчиняться подобным законам распределения). Опыт доказывает, что этого можно достичь, используя случайную сортировку по равномерному закону распределения и принцип «золотого сечения», т.е. примерное соотношение объемов указанных выборок - 0,46:0,32:0,22.
Здесь возможны два подхода: анализ в пространстве состояний и анализ в пространстве функций.
Первый подход основывается на регистрации значений характеристик, второй - анализом функциональной связи между ними.
Первый подход определяется вычислением рассмотренных напряженностей по значениям регистрируемых характеристик.
Второй подход основывается на том, что функциональные состояния подсистем различаются корреляционными связями между информационными (в том числе, системообразующими) характеристиками. Это различие наблюдается как в топологическом аспекте (одни связи исчезают, другие появляются), так и информационно-динамическом меняется сила влияния, ее направление, характер - линейный или нелинейный, детерминированный, вероятностный или хаотический, дискретный или аналоговый, с запаздыванием или без, парный или множественный и т.п.).
НФС вычисляется следующим образом. Пусть, для некоторого базового класса (например, «нормальное» функционирование) были идентифицированы различные математические зависимости, отражающие взаимосвязь значений регистрируемых показателей. Предполагаем, что упомянутые выше корреляционные сдвиги вызывают «сдвиги» и между структурами и параметрами математических (в простейшем случае - алгебраических) моделей. Тогда формулы (3), (4) или (6) можно использовать для вычисления НФС, осуществляя переход от исходного факторного пространства к виртуальному и рассматривая в качестве Хi значения квадрата относительного отклонения «истинного» (зарегистрированного) значения характеристики i от вычисленного по идентифицированным ранее (на этапе обучения) вышеуказанным математическим моделям.
После построения решающих правил соотнесения уровня напряженности ФС к определенному классу на экзаменационной выборке осуществляется идентификация функций принадлежности.
Заметим, что поскольку при анализе, БТС, как правило, имеют место статистически маломощные выборки исходных данных и классический регрессионный анализ не является адекватным при идентификации алгебраических моделей, то рекомендуется применять иные алгоритмы искусственного, например, метод группового учета аргументов.
В заключении можно отметить следующие практические приложения данной методологии, по которым получены результаты:
- диагностика по результатам общего анализа крови заболеваний печени, сердца, мочекаменной болезни, ОРЗ, туберкулеза;
- анализ напряжения ФС человека-оператора (ЭВМ);
- анализ экологической напряженности;
- анализ переходных процессов химических реакций;
- анализ переходных состояний диссипативных структур;
- анализ «усталости» искусственных органов в организме;
- анализ развития плода;
- анализ экономической напряженности работы фармацевтических служб;
- анализ выбора учебной траектории абитуриентом.
Библиографическая ссылка
Артеменко М.В., Протасова В.В., Оболенский А.Н. МЕТОДОЛОГИЯ ОЦЕНКИ СТЕПЕНИ НАПРЯЖЕННОСТИ ФУНКЦИОНАЛЬНОГО СОСТОЯНИЯ БИОТЕХНИЧЕСКИХ СИСТЕМ // Фундаментальные исследования. 2008. № 6. С. 94-97;URL: https://fundamental-research.ru/ru/article/view?id=3248 (дата обращения: 01.02.2026).



