Обычно для определения концентрации кластеров используется закон действующих масс. На наш взгляд, это не совсем корректно. В химии при реакции А + В получается новое вещество С. Причем, если идет цепочка реакций
A + B → C + B → D + C → E,
то из Е не получится А или В, а только D или С. В процессах кластеризации участвует одно и то же вещество, и из тетрамера, например, могут получиться при распаде как тримеры и мономеры, так и димеры. Кроме того, использование закона действующих масс – достаточно сложная процедура, связанная с подсчетом интеграла состояний, а для этого требуется знать геометрию кластера и его строение (подсчёт момента инерции, количество колебательных степеней свободы и частоты колебаний). По этой причине в данной статье предлагается другой способ расчёта концентрации кластеров через вероятности их распада и роста.
Определение сечения и вероятности захвата
Сечение захвата подсчитано по законам классической механики с использованием потенциала Леннарда–Джонса, к которому добавлен потенциал центробежной силы [1, 2]. В связи с тем, что прицельное расстояние ρ > σ, составляющая полной потенциальной энергии, соответствующая отталкиванию не учитывалась. В этом случае, взяв производную от
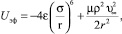(1)
по r и приравняв её нулю, получим
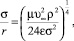(2)
где ε и σ – параметры потенциала взаимодействия кластера с мономером; μ – приведенная масса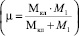 
, υ∞ – скорость мономера на бесконечности. Захват возможен, если энергия налетающей частицы в точности равна Uэфф при r = ρmax. Отсюда находим ρmax:
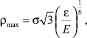(3)
где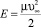 
– энергия налетающей частицы. Тогда сечение захвата будет
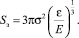(4)
Если сечение захвата умножить на поток падающих частиц, то получим вероятность захвата. Однако могут быть захвачены только те частицы, энергия которых меньше или равна Uэфф или определенного предела. Определим число таких частиц:
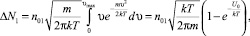
где n01 – концентрация мономеров.
Тогда вероятность захвата будет
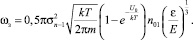
Усредним эту вероятность по энергиям
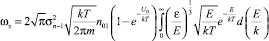
или
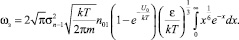
Интеграл равен
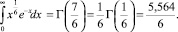
Тогда
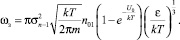(5)
Расчёт вероятности распада кластера
Определим вероятность распада кластера размерности n. Хотя распад кластера происходит под действием ударов внешних молекул, однако будем считать, что ударяющаяся частица образует вместе с кластером составную частицу. В этом кратковременном образовании скорости молекул распределены по Максвеллу. Энергия ударяющей частицы распределяется между всеми молекулами кластера и вылететь из него может только та, энергия которой больше энергии связи.
Число таких частиц, скорость которых больше предельно допустимой и направлена наружу, находится снова по распределению Максвелла [3,4]:
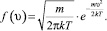
Функция f(υx) определяет число частиц, проекции скорости которых на ось х лежат в интервале (υx, υx + dυx): f(υx)dυx. Если это число умножить на n0υx, то получим число частиц, проходящих через единицу поверхности за единицу времени и имеющих υx, лежащую в указанном интервале. Общее число частиц, проходящих через единицу поверхности за 1 секунду и имеющих скорости больше минимальной υmin, равно
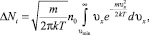
где n0 – число частиц в единице объёма кластера.
Взяв интеграл, получаем
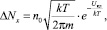(6)
где U0 – потенциальный барьер, который должна преодолеть вылетающая частица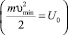 
. То есть
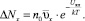
Это есть число частиц, прошедших через единицу поверхности кластера наружу за 1 секунду. Тогда через всю поверхность кластера пройдет число частиц
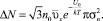(7)
Множитель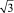 
появляется вследствие замены υx на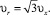 
Столько раз в секунду кластер может распасться. Следовательно, это выражение можно считать вероятностью распада кластера за единицу времени:
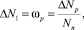
где ΔNp – число распавшихся в секунду кластеров размерности n. Поэтому
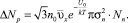(8)
Получение рекурентной формулы для концентраций кластеров.
При равновесии число вновь образованных кластеров размерности n равно числу распавшихся кластеров этой же размерности, т.е.
ΔNз = ΔNp или ωзNn–1 = ωpNn.
Значит
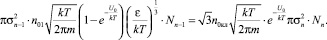(9)
Теперь можно найти связь между концентрациями кластеров размерности n – 1 и n. Под концентрацией кластеров понимается отношение
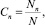
где N – число структурных единиц. Прежде чем вводить эту концентрацию, преобразуем n01:
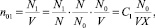
где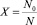 
– есть средний размер кластера. Учитывая это представление, (9) можно записать в виде:
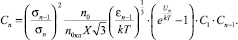(10)
Отношение n0/n0кл есть отношение плотностей газа и «жидкости», если считать кластер капелькой жидкости. Кроме того, отношение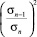 
равно отношению их размерностей в степени 2/3. В самом деле, так как
,
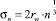где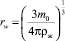 
– радиус Вигнера-Зейтца; m0 – масса одного атома или молекулы; ρж – плотность материала кластера в жидом состоянии. Таким образом, равенство (10) принимает вид:
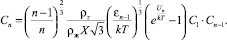(11)
Остается определиться с εn–1 и Un. Первое число – это есть глубина потенциальной ямы с обратным знаком в энергии взаимодействия мономера с кластером размерности n – 1, а второе – работа выхода мономера из кластера размерности n. Усреднение по всем направлениям ориентации димера, например, дает минимальную энергию взаимодействия – 0,5ε. Если комплекс состоит из n – 1 частиц, то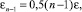 
где ε – параметр потенциала Леннарда–Джонса парного взаимодействия, который можно взять в [1] или [5]. При отрыве мономера из комплекса размерности n он взаимодействует с n – 1 частицами и, казалось бы, должно быть 
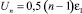. Однако, согласно Б.М. Смирнову [3] и нашим модельным расчётам, кластер в газах имеет фрактальную структуру, а не плотно упакованную. Следовательно, число соседей у мономера может быть либо один, либо два. Даже если число соседей равно двум, то Un ≤ 2ε. Следовательно, можно считать, что для всех кластеров Un ≈ ε (в первую очередь будут отрываться крайние частицы).
Учитывая зависимость εn–1 и Un от n, формулу (11) можно представить следующим образом:
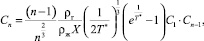(12)
где Т* – приведённая температура, равная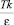 
; k – постоянная Больцмана.
В системе уравнений (12) неизвестным является средний размер кластера Х. В случае малых кластеров Х < 2. В первом приближении можно положить Х = 1. Если требуется большая точность, что можно, найдя Ск при Х = 1, определить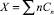 
, подставить в (12) и повторить вычисления.
Определение максимального размера кластера
В газах даже в состоянии насыщения слишком большие комплексы – редкость. При данном давлении и температуре должен быть максимальный размер кластера. Этот размер можно посчитать, если равенство ΔNз = ΔNp применить к одному и тому же кластеру. Равенство (5) можно трактовать как скорость роста кластера, а (8) – скорость распада кластера. Если эти соотношения записать для одного и того же n, приравнять их, то получим уравнение, определяющее n максимальное:
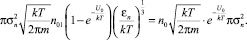(13)
Если считать, что n01 равно числу молекул в единице объёма, то отношение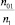 
равно отношению плотностей газа и жидкости. Тогда (13) перепишется в виде:
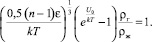(14)
Использование формулы (14) при U0 = ε дает максимальный размер кластера аргона в состоянии насыщения (Р = 40 бар, Т = 146°К) около 5000. Если же считать, что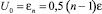 
, то максимальный размер кластера при тех же условиях равен 6. Отсюда следует, что приближение 
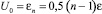относится к малым кластерам, а U0 = ε или 4ε÷6ε относится к большим кластерам. Большой кластер можно считать капелькой жидкости и поэтому у него U0 зависит лишь от числа соседних молекул, которое не зависит от n. При Р = 40 бар и Т = 146°К (состояние, близкое к критическому), оказывается, оба варианта значений U0 дают максимальный размер кластера близкий к двум. Получается, что в критическом состоянии комплексы молекул отсутствуют.
Выводы
Итак, из сказанного следует, что концентрацию комплексов в газах, которые не являются насыщенным паром, можно определять по формулам (12), ограничившись пятью уравнениями:
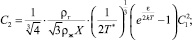
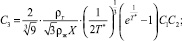(15)
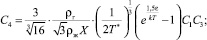
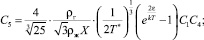
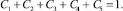(16)
Как выше уже говорилось, можно положить Х = 1. Чтобы компенсировать ошибку в расчётах при Х = 1, можно показатель экспоненты в скобках везде считать равным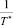 
.
Рецензенты:
Плотников С.В., д.ф.-м.н., профессор кафедры «Техническая физика», РГП на ПХВ Восточно-Казахстанский государственный технический университет имени Д. Серикбаева, г. Усть-Каменогорск;
Скаков М.К., д.ф.-м.н., заведующий кафедрой «Техническая физика», РГП на ПХВ Восточно-Казахстанский государственный технический университет имени Д. Серикбаева, г. Усть-Каменогорск;
Кульбачинский В.А., д.ф.-м.н., профессор кафедры физики низких температур и сверхпроводимости, физический факультет, Московский государственный университет им. М.В. Ломоносова, г. Москва.
Работа поступила в редакцию 24.06.2013.
Библиографическая ссылка
Павлов А.М. ОПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ МАЛЫХ КЛАСТЕРОВ В ГАЗАХ ЧЕРЕЗ ВЕРОЯТНОСТИ ИХ РАСПАДА И ЗАХВАТА МОНОМЕРОВ // Фундаментальные исследования. – 2013. – № 10-4. – С. 752-756;URL: https://fundamental-research.ru/ru/article/view?id=32395 (дата обращения: 16.04.2024).