Одним из ярких примеров функционирования сети является транспортная сеть. Математические модели, применяемые для анализа транспортных сетей, очень разнообразны по решаемым задачам, математическому аппарату, используемым данным и степени детализации описания движения [2]. Однако проблема эффективного управления транспортной сетью по-прежнему актуальна.
Моделирование и исследование транспортных потоков часто проводится с помощью теории конкурентного бескоалиционного равновесия, описывающего достаточно адекватный механизм функционирования автомобильных улично-дорожных сетей [2]. Такие модели позволяют получить прогнозные оценки по загрузке элементов транспортной сети и являются одним из инструментов определения эффективности проектов по реорганизации транспортной сети. Задача потокового равновесия сводится к поиску маршрутов сети с минимальными транспортными затратами, а сложность численного решения этих задач в свою очередь в основном зависит от аналитического задания функции транспортных затрат.
1. Граф-представление транспортной сети
Конкретизируем основные понятия, используемые в данной работе. Назовем сетевые потоки неконфликтными, если на данном участке сети они не пересекаются, и конфликтными – в противном случае. Вершинами графа будем считать узловые точки – точки, в которых либо расположены источники или потребители информации, либо происходит пересечение конфликтных потоков. То есть узловые точки образуются пересечением многоканальных магистралей. В работах [3, 5, 6] автор предлагает следующую ниже классификацию узловых точек (УТ).
Пусть одна часть потоков (назовем их главными) проходит через УТ беспрепятственно. Требования второй части потоков (второстепенных) ожидают возникновения достаточных интервалов по времени между требованиями главных потоков для пересечения УТ. Такая УТ названа узловой точкой первого типа или «нерегулируемое пересечение потоков требований».
Рассмотрим теперь узловую точку, в которой для возможности ее пересечения поочередно перекрывается движение для одной из групп неконфликтных потоков на фиксированное время. Это узловая точка второго типа или «регулируемое пересечение потоков требований».
Сетью называется граф, каждой дуге которого поставлено в соответствие некоторое число. Поток на графе – это некоторая функция, заданная на дугах графа. В разработанной автором модели поток на графе задается в виде функции плотности распределения интервалов по времени между следующими подряд требованиями. Ранее автором была рассмотрена модель функционирования сети, построенная на гипотезе о распределении интервалов по времени между требованиями в каждом из потоков по закону Эрланга. В данной работе модель распространена на случай, когда интервалы по времени распределены по обобщенному закону Эрланга. При правильном подборе параметров с помощью обобщенного закона Эрланга можно аппроксимировать практически любое распределение случайной величины.
2. Метод определения функции транспортных затрат для узловой точки сети типа «нерегулируемое пересечение потоков требований»
2.1. Обобщенный закон Эрланга распределения случайной величины
При обобщенном распределении Эрланга [4] интервал по времени между подряд идущими требованиями проходит k стадий T0, T1, ..., Tk–1, причем длительности этих стадий имеют показательные распределения с параметрами λ0, λ1, ..., λ k–1 соответственно. Преобразование Лапласа функции плотности распределения fk(t) имеет вид
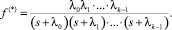
Если все параметры λi различны, функция распределения обобщенного закона Эрланга имеет вид
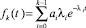
где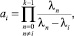 
причем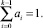 
Интегральная функция распределения
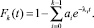
Математическое ожидание для обобщенного закона Эрланга может быть получено с учетом определения потока Эрланга:
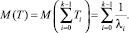
Дисперсия для обобщенного закона Эрланга может быть получена с учетом определения потока Эрланга:
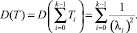
n-й начальный момент:
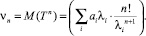
2.2. Расчет среднего значения времени обслуживания требований в узловой точке I типа при справедливости гипотезы о распределении интервалов по времени по обобщенному закону Эрланга
Пусть требованию второстепенного потока для продолжения движения требуется пересечь L главных потоков в условиях УТ I типа. Допустим, интервалы во времени в пересекаемых потоках распределены по обобщенному закону Эрланга k1, k2, ..., kL порядков с параметрами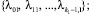 
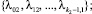
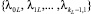соответственно. Учтем, что требование прибывает к УТ в случайный момент времени, независимо от требований остальных потоков. Обозначим через T0 минимальный временной интервал между подряд идущими требованиями в конфликтном потоке, который необходим требованию второстепенного потока для продолжения движения.
Пусть t – случайно выбранный нами момент времени и пусть Т* – интервал между двумя соседними случайными событиями, на который попала случайная точка t.
Т* = Q + R,
где R – время, оставшееся до наступления следующего события, а Q – время, прошедшее после последнего поступившего требования.
Тогда, согласно теории случайных процессов [1], вероятности того, что время Q, прошедшее после последнего прибытия требования, и время R, оставшееся до очередного прибытия, меньше некоторого наперед заданного значения Т0, выражаются формулами:
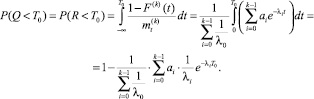
Следовательно, вероятность того, что за время Т0 не прибудет ни одно требование:
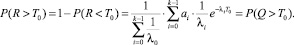
Числовые характеристики случайных величин Q и R: математическое ожидание:
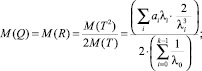
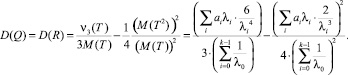
Теорема. Пусть в узловой точке первого типа требованию в потоке второстепенного направления необходимо пересечь L потоков главного направления;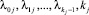 
– параметры обобщенного закона Эрланга для j-го пересекаемого потока, j = 1, 2, ..., L; T0 – минимальный временной интервал между подряд идущими требованиями в конфликтном потоке, который необходим требованию второстепенного потока для продолжения движения. Тогда для первого требования во второстепенном потоке среднее время обслуживания равно
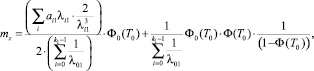
где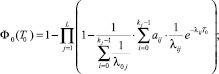 
Доказательство.
Рассмотрим величину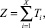 
, где T1 = R1 – время, оставшееся до прибытия очередного требования в первом пересекаемом потоке главного направления (поток (1)); Ti, i = 2, 3, 4, ... – интервал между прибытиями (i – 1)-го и i-го требований в потоке (1); X – целочисленная случайная величина, равная числу требований потока (1), которые необходимо пропустить, прежде чем продолжить движение (очевидно, что X = m, когда первые m временных интервалов меньше необходимого времени, а следующий (m + 1)-й уже больше Т0).
Введем следующие случайные величины:
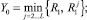
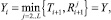i = 1, 2, 3, …
Здесь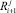 
– временной интервал в j-м потоке, оставшийся до прибытия (i + 1)-го требования в потоке (1). Функция распределения случайной величины Yj j = 1, 2, 3, ...имеет вид [1]:
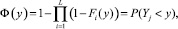
где Fi(y) – функция распределения i-й случайной величины.
Следовательно, функция распределения случайной величины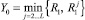 
:
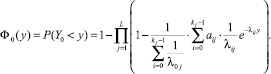
Функции распределения случайных величин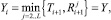 
i = 1, 2, 3, … совпадают и имеют вид:
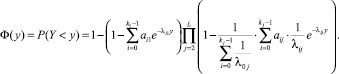
Следовательно,
.
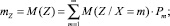
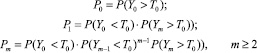То есть
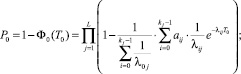
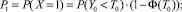
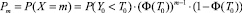при m ≥ 2.
Продолжим вычисления:
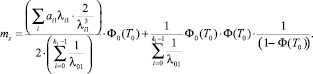
Теорема доказана
Узловая точка I-го типа может быть представлена как система массового обслуживания с неограниченной очередью. Поток заявок – это поток требований второстепенного потока, прибывающий к узловой точке; время обслуживания – время, проведенное требованием в ожидании возможности продолжить движение. Ранее [6] автором с применением метода псевдосостояний было доказано, что средняя задержка требования второстепенного потока в узловой точке I-го типа
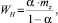
где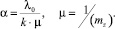 
2.3. Функция транспортных затрат для узловой точки I-го типа
Согласно теории потокового равновесия, для получения численных значений равновесного распределения потоков необходимо сначала решить проблему построения функции транспортных затрат. Самым распространенным предположением о свойствах функции транспортных затрат является логичное предположение о ее аддитивной зависимости от транспортных затрат на прохождение отдельных дуг и вершин.
Функцией транспортных затрат для узловой точки в зависимости от целей оптимизации могут быть выбраны:
1) 
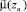– вес вершины zn (узловой точки) для потока данного направления;
2) μ(zn) – суммарный вес вершины zn (узловой точки);
3) μM(zn) – средняя задержка требования выбранных направлений.
Для узловой точки I типа
1) 
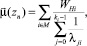, где М – множество выбранных направлений;
2) 
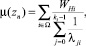, где Ω – множество всех направлений движения требований через данную УТ;
3) 
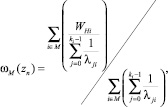где М – множество выбранных направлений.
Заключение
Результаты исследования, изложенные выше, являются обобщением проведенной автором работы по оптимизации распределения транспортных потоков по сети [5, 6]. Гипотеза о распределении интервалов по времени между требованиями по закону Эрланга позволила разработать математическую модель, дающую удовлетворительные по точности результаты оценивания качества функционирования сети. Кроме того, минимальный набор исходных параметров сделал менее дорогостоящей разработку базы данных для проведения оценки качества реорганизаций внутри сети. Обобщенный закон Эрланга при правильном подборе параметров позволит с достаточной точностью аппроксимировать практически любое распределение, а следовательно, даст возможность увеличить рамки применимости модели на потоки более высокой плотности при прохождении ими ряда узловых точек. Это в свою очередь увеличит точность при решении оптимизационных задач в теории транспортных потоков.
Работа выполнена при поддержке РФФИ, проект р-юг-а-13-08-96502.
Рецензенты:
Атрощенко В.А., д.т.н., профессор, декан факультета компьютерных технологий, ФГБОУ ВПО «Кубанский государственный технологический университет» Министерства образования и науки РФ, г. Краснодар;
Видовский Л.А., д.т.н., профессор, заведующий кафедрой вычислительной техники и автоматизированных систем управления, ФГБОУ ВПО «Кубанский государственный технологический университет» Министерства образования и науки РФ, г. Краснодар.
Работа поступила в редакцию 05.09.2013.
Библиографическая ссылка
Наумова Н.А. МЕТОД ОПРЕДЕЛЕНИЯ ФУНКЦИИ ТРАНСПОРТНЫХ ЗАТРАТ ДЛЯ УЗЛОВОЙ ТОЧКИ СЕТИ ТИПА «НЕРЕГУЛИРУЕМОЕ ПЕРЕСЕЧЕНИЕ ПОТОКОВ ТРЕБОВАНИЙ» // Фундаментальные исследования. – 2013. – № 10-4. – С. 717-722;URL: https://fundamental-research.ru/ru/article/view?id=32389 (дата обращения: 19.04.2024).