Роботы, перемещающиеся с отрывом от поверхности, являются объектами исследования многих ученых, таких как Б. Браун, Дж. Цеглин, С. Дубовский, П. Фиорини, М. Ковас, Д. Флориано [9–13], и крупных инженерных компаний, включая Бостон Дайнемикс [14]. Исследуемые роботы разнообразны по конструкции, массогабаритным параметрам, высоте и длине реализуемого прыжка. Но их можно классифицировать по ряду признаков: способам позиционирования до и после отрыва от поверхности, количеству звеньев, типу привода, посредством которого осуществляется разгон до отрыва от поверхности.
Среди способов позиционирования до полета наиболее распространенными являются поворот корпуса робота на колесах или ногах или же изменение угла наклона корпуса к поверхности за счет изменения положения его центра масс, а также поворот разгонного модуля относительно неподвижного корпуса. После приземления прыгающие роботы могут позиционироваться для достижения устойчивого положения, из которого возможна реализация следующего прыжка путем изменения геометрии звеньев устройства или же за счет изменения положения центра масс. Еще одним классификационным признаком прыгающих роботов является количество входящих в них звеньев. Различают роботов двух-, трех- и четырехзвенных. Для отрыва роботов от поверхности могут использоваться различные приводы: пневматические, гидравлические, с накопителями энергии, работающие на топливно-воздушной смеси, а по виду движения, совершаемого звеньями в момент разгона, различают пары вращательного и поступательного движения.
В данной работе рассматривается четырехзвенный прыгающий робот, разгон которого до отрыва от поверхности осуществляется парой поступательного движения, в качестве привода используется привод с накопителем энергии, причем в момент отрыва от поверхности с последней взаимодействует нога устройства, а при приземлении – корпус. Позиционирование объекта для реализации прыжка с заданными параметрами осуществляется путем поворота разгонного модуля относительно корпуса, позиционирования робота после приземления не требуется, т.к. следующий прыжок устройство может совершить с той из сторон корпуса, на которую произошло приземление. Приведен алгоритм моделирования одного прыжка объекта, представлены результаты, полученные численным путем.
Математическая модель прыгающего робота
Будем рассматривать прыгающего робота, состоящего из четырех звеньев 1–4, первое из которых является стопой, второе и третье образуют ногу, а четвертое представляет собой корпус (рис. 1). На звеньях 2 и 4 установлены приводы, обеспечивающие поворот звеньев 1 и 3 относительно звеньев 2 и 4. На звене 2 также установлен привод, позволяющий звеньям 2 и 3 поступательно перемещаться друг относительно друга [2, 7, 8].
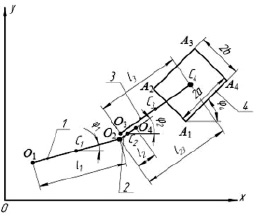
Рис. 1. Расчетная схема четырехзвенного прыгающего робота
Прыжок робота происходит в вертикальной плоскости Оху с горизонтальной шероховатой поверхности, совпадающей с осью Ох. При разработке математической модели будем считать, что звенья i = 1 – 3 объекта являются абсолютно твердыми стержнями длинами li, а звено 4 – абсолютно твердым прямоугольником А1А2А3А4 размерами 2a×2b. Масса mi каждого звена сосредоточена в центре его симметрии – точке Ci. Расстояние l23 между точками О2 и С4 соответствует длине ноги.
Положение центров масс звеньев робота определяется радиусами-векторами
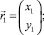 (1)
(1)
 (2)
(2)
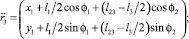 (3)
(3)
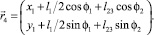 (4)
(4)
Положение звеньев робота описывается вектором координат [7]
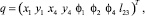 (5)
(5)
где x1, y1, x4, y4 – координаты центров масс звеньев 1 и 4, φ1, φ2 и φ4 – углы поворота звеньев 1, 2 и 4, l23 – длина ноги робота. Углы φ1 и φ2 представляют собой углы между звеньями 1, 2 и положительным направлением оси Ох. Угол φ4 представляет собой угол, под которым сторона корпуса А1А4 наклонена к горизонтальной оси.
Для записи системы дифференциальных уравнений движения объекта используются уравнения Лагранжа второго рода. Кинетическая энергия системы определяется по формуле
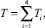 (6)
(6)
где i = 1–4 – звенья робота.
Каждое звено робота совершает плоское движение, поэтому кинетическая энергия i-го звена вычисляется следующим образом
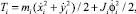 (7)
(7)
где 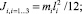
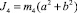 – центральные моменты инерции звеньев;
– центральные моменты инерции звеньев; 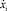 ,
, 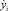 – проекции скорости центра масс i-ого звена на оси системы координат;
– проекции скорости центра масс i-ого звена на оси системы координат;  – угловая скорость i-го звена.
– угловая скорость i-го звена.
Система дифференциальных уравнений движения робота может быть записана в матричной форме
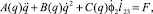 (8)
(8)
где A(q), B(q), C(q) – матрицы коэффициентов; F – матрица обобщенных сил.
Прыжок устройства состоит из последовательности семи этапов, каждый из которых характеризуется определенным видом движения звеньев [5, 6]. Во время этапов 1–3 происходит позиционирование объекта для совершения прыжка, при этом корпус робота взаимодействует с поверхностью, а разгонный модуль, состоящий из звеньев 1–3, меняет свое положение относительно корпуса для реализации прыжка под требуемым углом к горизонту. Четвертый этап соответствует разгону устройства, во время которого звено 1 находится на поверхности, а звенья 3 и 4 приобретают скорость, достаточную для отрыва робота от поверхности. Этап 5 характеризует движение робота с отрывом от поверхности, при этом наблюдается втягивание звеньев 1 и 2 в корпус, а этапы 6 и 7 – приземление объекта на корпус и его позиционирование до тех пор, пока одна из сторон корпуса не будет лежать на поверхности.
На геометрические размеры звеньев робота наложены ограничения, обусловленные последовательностью этапов движения
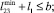
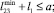 l2 ≤ b; l2 ≤ a;
l2 ≤ b; l2 ≤ a;
l3 ≤ b; l3 ≤ a; 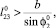 (9)
(9)
где 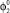 – угол наклона звена 2, при котором происходит разгон объекта до его отрыва от поверхности.
– угол наклона звена 2, при котором происходит разгон объекта до его отрыва от поверхности.
Прыжок исследуемого робота является программно-управляемым, причем управление осуществляется на этапах 1–5, когда происходит позиционирование и разгон устройства для отрыва от поверхности, а также непосредственно полет, этапы 6 и 7, во время которых осуществляется приземление, являются неуправляемыми. Управляющими воздействиями являются моменты, формируемые приводами вращательного движения, которые обеспечивают повороты звеньев робота на требуемые углы, а также сила, создаваемая линейным приводом, за счет которой происходит относительное перемещение звеньев 2 и 3. В данной работе будем рассматривать случай, когда указанные величины являются кусочно-постоянными функциями, численные значения которых на каждом из этапов прыжка являются константами.
Модель взаимодействия с поверхностью
При реализации одного прыжка робот взаимодействует с шероховатой поверхностью звеном 1 или 4 на одних этапах и перемещается с отрывом от поверхности на других. Будем считать, что при нахождении звена 1 или 4 на поверхности возникают распределенные силы трения и нормальной реакции, которые приводятся к центру приведения – точке К, расположение которой на данном этапе исследований не рассматривается. Сила взаимодействия данной точки с поверхностью может быть описана различными моделями трения: сухое кулоново трение, трение с непрерывно падающей характеристикой (некулоново трение), трение с уменьшенной динамической составляющей [3, 4]. Будем рассматривать случай, когда в точке К при взаимодействии с поверхностью будет возникать сила сухого трения, изменяющаяся по закону [1]:
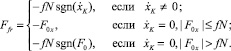 (10)
(10)
где F0x – горизонтальная проекция равнодействующей всех сил, кроме силы сухого трения, приложенных к звену, которое взаимодействует с поверхностью; f – коэффициент трения скольжения; N – нормальная реакция в опорной точке К; 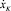 – скорость точки К вдоль оси Ох.
– скорость точки К вдоль оси Ох.
Будем рассматривать случай, когда модуль возникающей силы трения всегда меньше предельного значения 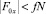 , скольжение тела по поверхности отсутствует. Силами вязкого сопротивления в данной работе будем пренебрегать.
, скольжение тела по поверхности отсутствует. Силами вязкого сопротивления в данной работе будем пренебрегать.
Алгоритм моделирования движения робота
Моделирование движения робота проводится по алгоритму, приведенному на рис. 2, 3. Определение этапа прыжка, в котором находится объект, осуществляется при помощи счетчика n. Значение n = 1 соответствует первому этапу, заключающемуся в повороте ноги до достижения угла 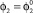 . После этого объект переходит во второй этап при n = 2, на котором стопа робота поворачивается до тех пор, пока не станет параллельной опорной поверхности (
. После этого объект переходит во второй этап при n = 2, на котором стопа робота поворачивается до тех пор, пока не станет параллельной опорной поверхности (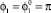 – для прыжка вперед).
– для прыжка вперед).
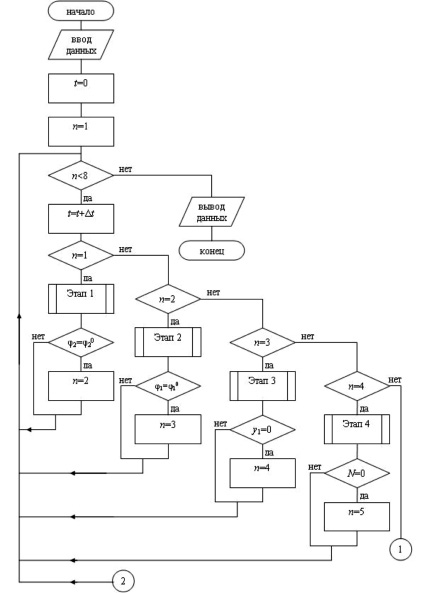
Рис. 2. Алгоритм моделирования одного прыжка робота (начало)
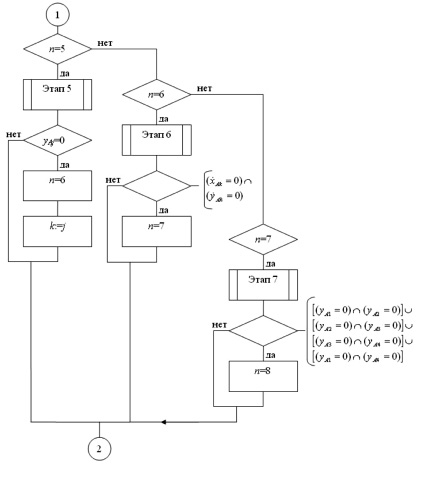
Рис. 3. Алгоритм моделирования одного прыжка робота (конец)
После выполнения указанного условия счетчик увеличивается на единицу n = 3, объект находится в третьем этапе, который заканчивается при достижении стопой опорной поверхности – y1 = 0. Четвертый этап (n = 4), во время которого объект разгоняется, завершается в момент отрыва стопы от поверхности, чему соответствует выполнение условия N = 0, начинается пятый этап (n = 5) движения устройства до тех пор, пока одна из точек корпуса Aj, j = 1–4 не начнет взаимодействовать с поверхностью 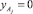 .
.
При приземлении происходит обнуление скорости точки (точек) контакта с поверхностью, чему соответствует шестой этап движения робота (n = 6), а затем (n = 7) наблюдается движение, которое закончится после того, как одна из сторон корпуса станет взаимодействовать с поверхностью.
Результаты численного моделирования
Преобразуем разработанную математическую модель реализации одного прыжка робота к безразмерному виду, используя масштабные коэффициенты: М = 0,05 кг, Т = 0,1 с, L = 0,1 м. Объектом моделирования является прыгающий робот, массы и геометрические размеры звеньев которого равны: m1 = 1, m2 = 1, m3 = 1, m4 = 7, а = 1, b = 1, l1 = 0,5, l2 = 0,9, l3 = 0,9. Начальными условиями моделирования являются следующие: t = 0, x4 = a, 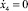 , y4 = b,
, y4 = b, 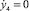 , φ4 = 0,
, φ4 = 0, 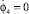 , φ1 = π,
, φ1 = π, 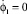 , φ2 = π/2,
, φ2 = π/2, 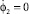 .
.
Для тестирования разработанных алгоритма и программы моделирования прыжка робота был рассмотрен случай, когда во время этапа полета не происходит втягивания звеньев ноги в корпус. Это соответствует движению робота как материальной точки, брошенной под углом к горизонту.
а 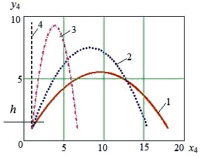 б
б 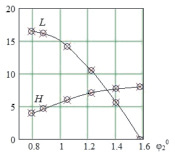
в 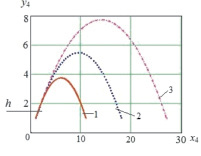 г
г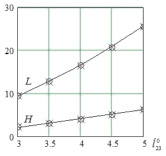
Рис. 4. а, в – траектории движения центра масс корпуса при отсутствии втягивания ноги в полете, полученные программно, при а – 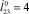 , h = 1,5: 1 –
, h = 1,5: 1 – 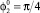 , 2 –
, 2 – 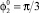 , 3 –
, 3 – 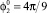 , 4 –
, 4 – 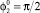 , в –
, в – 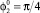 , h = 1,5: 1 –
, h = 1,5: 1 – 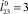 , 2 –
, 2 – 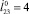 , 3 –
, 3 – 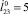 , б, г – зависимости
, б, г – зависимости 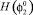 ,
, 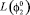 ,
,  – программные,
– программные,  – аналитические
– аналитические
Вращения корпуса в полете относительно его центра масс не происходит в связи с тем, что разгоняющая сила проходит через точку С4. Было проведено сравнение рассчитанных в программе высоты H и длины L прыжка объекта, под которыми понимались наибольшие расстояния вдоль осей Оу и Ох с момента отрыва звена 1 от поверхности до завершения прыжка, с вычисленными аналитическим способом высотой и дальностью полета тела, брошенного под углом к горизонту, результаты которого приведены на рис. 4. На данном и последующих рисунках приняты обозначения: 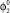 – угол наклона ноги к оси Ох, под которым приложена сила, осуществляющая отрыв робота от поверхности,
– угол наклона ноги к оси Ох, под которым приложена сила, осуществляющая отрыв робота от поверхности, 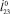 – скорость робота в момент начала этапа полета, h – значение ординаты центра масс корпуса робота в момент отрыва последнего от поверхности.
– скорость робота в момент начала этапа полета, h – значение ординаты центра масс корпуса робота в момент отрыва последнего от поверхности.
По приведенным графикам видно, что относительная погрешность между значениями высоты и длины прыжка, определенными программно и аналитически, не превышает 0,5 %, что свидетельствует о достаточной точности разработанных алгоритма и программы.
а 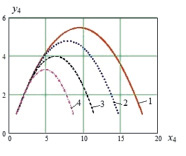 б
б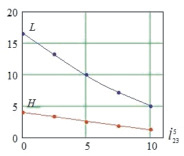
 г
г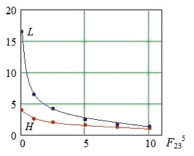
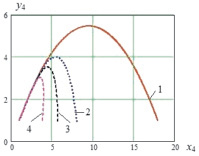
Рис. 5. а, в – траектории центра масс корпуса робота при а – 1 – 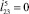 , 2 –
, 2 – 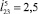 , 3 –
, 3 – 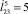 , 4 –
, 4 – 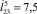 , в – 1 –
, в – 1 – 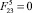 , 2 –
, 2 – 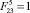 , 3 –
, 3 – 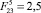 , 4 –
, 4 – 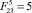 , б, г – высота и длина прыжка в зависимости от б –
, б, г – высота и длина прыжка в зависимости от б – 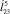 , г –
, г – 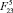
Так как при реализации прыжка роботом звенья ноги будут втягиваться в корпус во время полета, это движение будет оказывать влияние на траекторию центра масс корпуса и на значения высоты и длины прыжка. Рассмотрим два способа втягивания ноги в полете: с постоянной скоростью 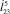 и под действием постоянной силы
и под действием постоянной силы 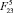 . На рис. 5 приведены траектории движения точки С4 и зависимости высоты и длины прыжка от значений
. На рис. 5 приведены траектории движения точки С4 и зависимости высоты и длины прыжка от значений 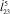 и
и 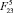 .
.
По графикам рис. 5, а, в видно, что траектория прыжка робота при равномерном втягивании ноги в корпус имеет вид параболы, выпуклость которой направлена вверх, втягивание ноги под действием силы сильно меняет характер траектории.
Прыжок на наибольшие высоту и длину происходит при отсутствии втягивания ноги в полете, а с увеличением скорости 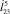 и силы
и силы 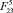 высота и длина прыжка убывают по некоторым криволинейным зависимостям (рис. 5, б, г), причем при постоянной скорости
высота и длина прыжка убывают по некоторым криволинейным зависимостям (рис. 5, б, г), причем при постоянной скорости 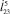 кривая убывает достаточно плавно, а при действии силы
кривая убывает достаточно плавно, а при действии силы 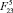 вначале наблюдается резкое падение высоты и длины прыжка, а затем их плавное убывание.
вначале наблюдается резкое падение высоты и длины прыжка, а затем их плавное убывание.
Заключение
В статье рассмотрен четырехзвенный прыгающий робот, состоящий из корпуса, ноги, образованной двумя звеньями, и стопы, прыжок устройства представлен в виде последовательности этапов, характеризующихся определенными видами движений звеньев. Для указанного объекта разработана математическая модель, в соответствии с которой осуществлено численное моделирование прыжка устройства по специальному алгоритму.
В статье приведены результаты движения робота в полете как материальной точки, для этого случая проведено тестирование алгоритма и программы, которое показало высокую сходимость с данными аналитического решения. Выявлено влияние на траекторию движения робота и на значения высоты и длины прыжка скорости втягивания звеньев ноги в полете, а также силы, под действием которой это втягивание осуществляется.
Работа выполнена в рамках гранта РФФИ № 10-08-00769-а, госконтракта № П699 тема № 1.109.10ф.
Рецензенты:
Кобелев Н.С., д.т.н., профессор, заведующий кафедрой теплогазоснабжения и вентиляции, ЮЗГУ, г. Курск;
Игнатенко Н.М., д.т.н., профессор, заведующий кафедрой общей и прикладной физики, ЮЗГУ, г. Курск.
Работа поступила в редакцию 07.08.2013.



