В работах [3, 4] предложены математические определения псевдоэмоции робота, эмоционального псевдовоспитания, уровней псевдовоспитания, относительной невосприимчивости робота к псевдовоспитанию с учетом коэффициентов кратковременной памяти робота. Математические модели основаны на гипотезе грузинского психолога Д.Н. Узнадзе [1, 2, 5].
Из работы [4] следует, что псевдоэмоция робота M(t) является непрерывной функцией на отрезке [0, t], а, следовательно, интегрируемой на этом отрезке.
Определение 1. Элементарным псевдовоспитанием робота r(t) назовем функцию вида
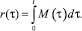 (1)
(1)
Определение 2. Эмоциональным псевдовоспитанием (далее псевдовоспитанием) робота R(t) (псевдовоспитание робота во время действия псевдоэмоции) назовем функцию вида
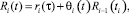 (2)
(2)
где t – текущее время, t > ti, 0 ≤ θi(t) ≤ 1. Текущее время удовлетворяет соотношению t = τ + ti, где τ – текущее время действия настоящей псевдоэмоции от начала ее проявления; ti – общее время действия всех предыдущих псевдоэмоций; ri(τ) и Ri(ti) – элементарное певдовоспитание и псевдовоспитание соответственно полученные роботом за время ti.
Определение 3. Такт – продолжительность во времени одной псевдоэмоции робота [3].
Советский психолог Д.Н. Узнадзе [2] выдвинул гипотезу о существовании у человека установок. Он пишет [5], что человек осуществляет те акты и процессы, то поведение, установка на которые выработалась у него под воздействием ситуации. Взаимодействие живого существа и среды может быть представлено следующим образом: на живое существо, движимое импульсом удовлетворения определенной потребности, начинает воздействовать внешняя ситуация и вызывает в нем соответствующее ситуации целостное изменение – определенную установку.
В теории эмоциональных роботов используются некоторые положения теории Д.Н. Узнадзе об установках. Так, свойства установок человека были использованы для моделирования процесса псевдовоспитания робота.
В теории эмоциональных роботов установке человека ставится в соответствие элементарное псевдовоспитание робота, значение которого постоянно в течение определенного количества тактов, т.е. ri = q. Для таких тактов псевдоэмоции робота являются равноценными. В теории эмоциональных роботов qq называется псевдоустановкой робота.
Определение 4. Уровнем псевдовоспитания робота назовем количество смен псевдоустановок робота к текущему такту процесса псевдовоспитания.
Для алгоритма Узнадзе в работе [3] введено допущение о равенстве и постоянстве коэффициентов кратковременной памяти θ, соответствующих конечному моменту времени каждой эмоции и предложены определения уровня псевдовоспитания робота k.
В статье [3] рассматривается процесс псевдовоспитания робота с равными коэффициентами памяти на каждом уровне псевдовоспитания робота, т.е. 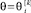 , причем элементарные псевдоэмоции роботов являются равноценными и положительными на каждом уровне псевдовоспитания, т.е.
, причем элементарные псевдоэмоции роботов являются равноценными и положительными на каждом уровне псевдовоспитания, т.е. 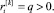
В статье [3] доказано, что последовательность (2) является сходящейся и вычисляется «предельное псевдовоспитание робота» на каждом уровне псевдовоспитания U[k].
Для перехода с одного уровня псевдовоспитания робота на другой вычисляется величина отклонения предельного псевдовоспитания от псевдовоспитания работа в конце текущего такта. В случае если величина отклонения меньше ε, осуществляется переход на новый уровень псевдовоспитания. Критерием перехода с уровня на уровень является выполнение неравенства:
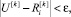 (3)
(3)
где ε – абсолютная невосприимчивость робота к псевдовоспитанию [3].
Процесс псевдовоспитания робота при переходе с одного уровня на другой описывает алгоритм Д.Н. Узнадзе [3]. Однако, согласно работам Д.Н. Узнадзе и его учеников [1, 2, 5], существуют периоды жизни человека, при котором установки не меняются, хотя в определенные моменты жизни человека могут изменяться. Поэтому алгоритм Узнадзе, предложенный в статье [3], необходимо усовершенствовать.
Алгоритм Узнадзе с учетом смены знака псевдоустановки робота
Рассмотрим алгоритм Д.Н. Узнадзе с учетом смены знака псевдоустановки робота q в конце тактов внутри уровня псевдовоспитания робота, между уровнями, а также вариант смены знака, который учитывает оба этих случая одновременно.
Пусть робот является равномерно забывчивым с равными коэффициентами эмоциональной кратковременной памяти внутри уровня псевдовоспитания робота k, т.е. 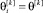 . Предположим, что для всех уровней его эмоции таковы, что на каждом уровне для разных тактов пвесдоустановки робота равны по модулю и могут отличаться знаком.
. Предположим, что для всех уровней его эмоции таковы, что на каждом уровне для разных тактов пвесдоустановки робота равны по модулю и могут отличаться знаком.
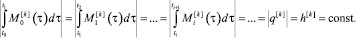 (4)
(4)
В качестве критерия перехода с одного уровня псевдовоспитания робота на другой будем использовать следующее правило [6]: точка перехода с уровня псевдовоспитания k на уровень k + 1 достигается, когда на уровне псевдовоспитания робота k изменение псевдовоспитания робота становится меньше некоторой величины δ, т.е. выполняется неравенство:
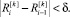 (5)
(5)
Определение 5. Опыт робота – псевдовоспитание робота, которое он получил на предыдущем уровне псевдовоспитания.
Опыт робота обозначим B. Будем считать, что при вычислении псевдовоспитания робота на первом уровне опыт робота равен нулю, т.е. B[0] = 0.
Введем индикатор случайных чисел 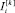 , который на каждом такте i каждого уровня псевдовоспитания k случайным образом принимает значения 1 либо –1. Аналогично определим индикатор случайных чисел J[k], который случайным образом принимает значения 1 либо –1 на каждом уровне псевдовоспитания k.
, который на каждом такте i каждого уровня псевдовоспитания k случайным образом принимает значения 1 либо –1. Аналогично определим индикатор случайных чисел J[k], который случайным образом принимает значения 1 либо –1 на каждом уровне псевдовоспитания k.
Знак псевдоустановки робота будем определять за счет 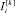 , т.е.
, т.е. 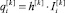 и
и 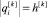 . Из цепочки равенств
. Из цепочки равенств 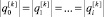 следует
следует 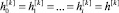 . Знак смены псевдовоспитания между уровнями будем вводить за счет опыта робота, умноженного на индикатор J[k] на каждом уровне.
. Знак смены псевдовоспитания между уровнями будем вводить за счет опыта робота, умноженного на индикатор J[k] на каждом уровне.
Алгоритм выполняется до тех пор, пока номер такта i не достигнет заданного количества тактов T, что является временем процесса псевдовоспитания робота.
Задаются время процесса псевдовоспитания робота T, уровень псевдовоспитания робота k = 1, номер такта i = 0.
Шаг 1. Задается h[1], θ[1], B[0] = 0.
Шаг 2. Вычисляется
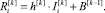
Шаг 3. Увеличивается на единицу i и вычисляется псевдовоспитание
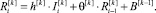
Шаг 4. Если не выполняется критерий перехода на следующий уровень псевдовоспитания 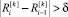 и если i < T, то переход к шагу 4.
и если i < T, то переход к шагу 4.
Шаг 5. Если выполняется 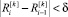 и если i < T, то k увеличивается на единицу, задаются h[k], θ[k], вычисляется опыт робота
и если i < T, то k увеличивается на единицу, задаются h[k], θ[k], вычисляется опыт робота 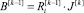 , i увеличивается на единицу. Переход к шагу 3.
, i увеличивается на единицу. Переход к шагу 3.
Шаг 6. Если i = T, то КОНЕЦ.
Вывод формулы псевдовоспитания робота на основе псевдоустановки и коэффициента эмоциональной кратковременной памяти внутри одного уровня псевдовоспитания
В рамках одного уровня псевдовоспитания робота псевдовоспитание можно записать следующим образом.
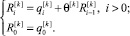 (6)
(6)
Систему уравнений (6) перепишем в виде суммы последовательности
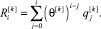 (7)
(7)
Предположим, что 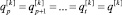 , где 0 ≤ p ≤ t ≤ i. Отсюда следует, что выполняются равенства
, где 0 ≤ p ≤ t ≤ i. Отсюда следует, что выполняются равенства 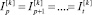 .
.
Обозначим разность 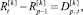 , тогда верно равенство
, тогда верно равенство
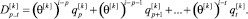 (8)
(8)
Таким образом, знак псевдоустановки робота не меняется для всех слагаемых 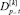 .
.
Умножим последовательность (8) на θ[k]
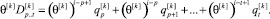 (9)
(9)
Рассмотрим разность (9) и (8)
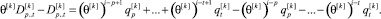 (10)
(10)
По условию
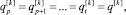
поэтому
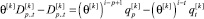
и
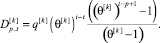 (11)
(11)
Очевидно, что при p = 0, t = i, q[k] = const будут выполняться следующие равенства:
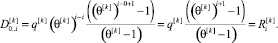
Представим 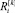 в следующем виде:
в следующем виде:
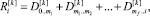 (12)
(12)
где ms – номер смены знака псевдоустановки робота, где 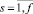 , f – количество смен знака псевдоустановки робота за время псевдовоспитания робота от 0 до i. Знак псевдоустановки робота всех слагаемых
, f – количество смен знака псевдоустановки робота за время псевдовоспитания робота от 0 до i. Знак псевдоустановки робота всех слагаемых 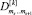 определяется индикатором
определяется индикатором 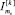 .
.
Подставим (11) в (12). В результате получаем формулу вычисления псевдовоспитания робота на основе псевдоустановки и коэффициента эмоциональной кратковременной памяти робота внутри одного уровня псевдовоспитания
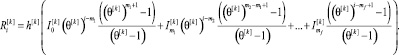 (13)
(13)
Достаточное условие перехода псевдовоспитания робота на следующий уровень при смене знака псевдоустановки внутри уровня псевдовоспитания
Рассмотрим разность на двух соседних тактах на одном уровне псевдовоспитания робота 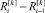 , используя формулу (13). После преобразований получаем
, используя формулу (13). После преобразований получаем
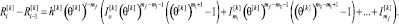 (14)
(14)
В (14) каждое слагаемое 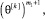 ,
, 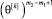 ,…,
,…, 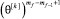 заменим на единицу и представим критерий перехода с одного уровня псевдовоспитания робота k на уровень k + 1 в виде:
заменим на единицу и представим критерий перехода с одного уровня псевдовоспитания робота k на уровень k + 1 в виде:
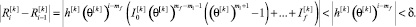
Получаем достаточное условие перехода с уровня псевдовоспитания робота k на уровень k + 1 при условии смены знака псевдоустановки
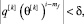 (15)
(15)
где q[k] и θ[k] – псевдоустановка робота и коэффициент эмоциональной кратковременной памяти работа на уровне псевдовоспитания робота k, mf – номер последнего такта от 0 до i, в который произошла смена знака псевдоустановки.
Достаточное условие того, что псевдовоспитание робота не переключится на следующий уровень псевдовоспитания
В (14) заменим каждый множитель 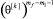 ,
, 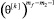 ,…,
,…, 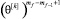 на ноль и рассмотрим следующую цепочку неравенств:
на ноль и рассмотрим следующую цепочку неравенств:
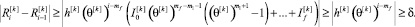
Достаточное условие того, что псевдовоспитание робота не переключится на следующий уровень, будет выглядеть следующим образом:
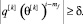 (16)
(16)
Вывод формулы псевдовоспитания робота на нескольких уровнях с учетом смены знака псевдоустановки
Пусть s1, s2,…, sk-1 – номера тактов, после которых происходит переключение с одного уровня псевдовоспитания на другой. Очевидно, что при выполнении неравенства 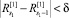 происходит переход псевдовоспитания с уровня k = 1 на уровень k = 2, а такт i = s1 + 1 является первым тактом уровня k = 2. Не уменьшая общности, предположим, s0 + 1 = 0.
происходит переход псевдовоспитания с уровня k = 1 на уровень k = 2, а такт i = s1 + 1 является первым тактом уровня k = 2. Не уменьшая общности, предположим, s0 + 1 = 0.
В рамках нескольких уровней псевдовоспитание можно записать следующим образом:
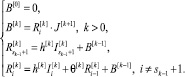 (17)
(17)
Систему уравнений (17) перепишем в виде суммы последовательности. Для первого уровня псевдовоспитание и опыт будет вычисляться следующим образом:
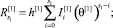 (18)
(18)
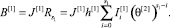 (19)
(19)
Для второго уровня псевдовоспитание и опыт будет вычисляться следующим образом:
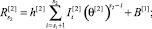 (20)
(20)
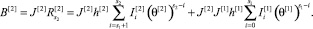 (21)
(21)
Обобщив вычисление опыта робота для уровня k – 1 на основе (18–21), получаем следующее равенство:
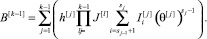 (22)
(22)
На основе (18–22) получаем формулу для вычисления псевдовоспитания такта x уровня k.
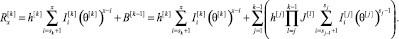 (23)
(23)
Заключение
Таким образом, в настоящей статье на основе гипотезы грузинского психолога Д.Н. Узнадзе вводится алгоритм вычисления псевдовоспитания робота с учетом смены знака псевдоустановки внутри и между уровней псевдовоспитания робота. Доказываются достаточные условия, описывающие возможность или невозможность перехода с одного уровня псевдовоспитания робота на другой уровень соответственно.
Рецензенты:
Пенский О.Г., д.т.н., доцент, профессор кафедры процессов управления и информационной безопасности Пермского государственного национального исследовательского университета, г. Пермь;
Ясницкий Л.Н., д.т.н., профессор, заведующий кафедрой прикладной информатики Пермского государственного гуманитарно-педагогического университета, г. Пермь.
Работа поступила в редакцию 01.08.2013.
Библиографическая ссылка
Шарапов Ю.А. МОДЕЛИ СМЕНЫ ЗНАКА ПСЕВДОУСТАНОВКИ РОБОТА // Фундаментальные исследования. 2013. № 10-1. С. 77-81;URL: https://fundamental-research.ru/ru/article/view?id=32219 (дата обращения: 16.02.2026).



