Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Снопов А.И. 1

---

1 ФГАОУ ВПО «Южный федеральный университет Министерства науки и образования России»

Приводятся результаты исследований на основе уравнений Навье–Стокса изотермических течений вязких газов в прямых микроканалах. Показано, что строго одномерные изотермические потоки вязких газов в таких каналах не могут быть реализованы при любых связях между коэффициентами объемной и сдвиговой вязкости. Указаны условия, при которых потоки газов в прямых микроканалах можно рассматривать как одномерные. Эти условия включают ограничения на поперечные размеры микроканалов, на перепады квадратов давлений газа на входе в микроканал и на выходе из него, на величины температуры газа, а также на его термодинамические параметры. Изложен метод расчета таких одномерных потоков газа, основанный на линеаризации уравнений движения газа в микроканалах, приводящей к разделению переменных, аналогичному случаям течений несжимаемых жидкостей в прямых трубах произвольного сечения. Представлены формулы для определения расходов газа через микроканалы правильных треугольных, прямоугольных, эллиптических и полуэллиптических сечений. Изложен общий метод расчета потоков вязкого газа в микроканалах произвольной формы сечения.

Статья в формате PDF

883 KB

вязкость

газ

течение микроканал

расчет

1. Елизарова Е.Г. Квазигазодинамические уравнения и методы расчета вязких течений. – М. Научный Мир, 2000. – 350 с.

2. Лойцянский Л.Г. Механика жидкости и газа. – 7-е изд., исправ. – М.: ДРОФА, 2003. – 846 с.

3. Снопов А.И. Теоретические основы работы газостатических опор. – Ростов н/Д, ЮФУ, 2009. – 176 с.

4. Снопов А.И., Дубовицкий В.С. Течение газа в микрощели // Международный журнал экспериментального образования. – 2011. – № 6. – С. 81–82.

5. Тимофеев Д.П. Кинетика адсорбции. – М.: Из-во АН СССР, 1962. – 252 с.

Первые теоретические исследования течений газов в микроканалах были проведены в 50-х годах прошлого века при разработке теории диффузии газов в пористых средах [5] и теории газовой смазки [3]. В настоящее время интерес к этой теме сохраняется в связи с развитием исследований по течению разреженных газов [1] и расчетам утечек газа из резервуаров и транспортных систем через микрощели [4].

При моделировании потоков вязкого газа в прямых микроканалах обычно используются допущения, лежащие в основе исследований одномерных потоков вязкой несжимаемой жидкости. Это приводит к выводу о независимости скорости потока от продольной координаты [1, 5], что приводит к противоречию известному факту возрастания скорости газового потока в направлении выхода из канала. Фактически используются формулы для пуазейлевского течения в круглых трубах и плоских каналах. Формулы для газового потока получаются из формул для потока несжимаемой жидкости с помощью замены плотности несжимаемой жидкости на полусумму плотностей газа на входе и выходе из канала. Отсутствуют какие-либо количественные оценки области применимости предложенных моделей.

Указанных недостатков можно избежать, если для анализа течения газа в микроканалах использовать полные уравнения Навье–Стокса для вязкого газа, дополненные уравнениями неразрывности и состояния [3] при допущении об изотермичности потока (T = const)

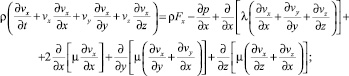
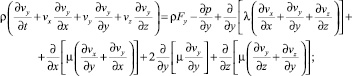(1)

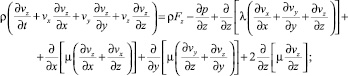
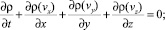p = RTρ;

здесь vx, vy, vz– компоненты скоростей частиц газа в декартовой системе координат; ρ – плотность; Т – абсолютная температура; R – газовая постоянная, определяемая по формуле R = Cp – CV. Cp и CV– удельные теплоемкости газа при постоянном давлении и постоянном объеме соответственно, принимаемые постоянными. Fx, Fy, Fz – компоненты массовых сил, λ и μ – коэффициенты объемной и сдвиговой вязкостей газа соответственно.

Особенностью уравнений движения вязкого газа является нечеткость в определении понятия параметра p, иногда называемого давлением. Согласно распространенной гипотезе Стокса, параметр p является средним арифметическим значением нормальных напряжений на трех взаимно ортогональных площадках, проходящих через заданную точку потока, чем допускается неравенство величин нормальных напряжений на этих площадках. Значение коэффициента объемной вязкости существенно зависит от определения смысла параметра р. Из гипотезы Стокса следует, что 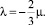Иногда параметр λ принимают не зависимым от μ или используют другие связи между λ и μ. С учетом сказанного остается неясным, какой параметр р присутствует в последнем уравнении системы (1) – уравнении состояния.

Ниже представлены результаты исследований установившихся потоков газа в прямых микроканалах, проведенных на основе уравнений (1–3) в рамках общепринятых допущений об их одномерности и отсутствия внешнего силового поля, что позволило принять коэффициенты вязкости газа μ и λ постоянными. Показано, что потоки вязких газов в микроканалах в отличие от несжимаемой жидкости не могут быть строго одномерными и установлены ограничения, при которых их можно рассматривать как квазиодномерные. Изложен метод определения расходов газа через микроканалы произвольных форм сечений и представлены формулы для частных случаев.

Для прямых микроканалов «естественно допустить», что поток газа в них одномерный. Если ось направлена вдоль канала в сторону течения, то можно принять, что

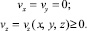(2)

При этом из уравнений (1–2) следуют равенства

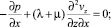
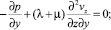
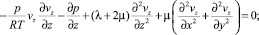(3)

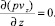
Первые два равенства полученной системы позволяют ввести в рассмотрение новую функцию P(z), зависящую только от продольной координаты z

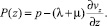(4)

Воздействие газа на стенку микроканала определяется компонентами тензора напряжений. Если стенка гладкая, то можно для любой точки О этой стенки выбрать местную систему координат такую, чтобы ось Оz проходила по стенке вдоль микроканала, а оси Ох и Оу лежали в плоскости, перпендикулярной оси Оz, и располагались так, чтобы ось Ох была ортогональна стенке и направлена наружу микроканала. Нормальное напряжение τxx, действующее на частицу жидкости, прилегающую к стенке канала в точке О, определяется по формуле

.

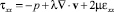В силу (2) имеем 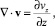εxx = 0. Из условия прилипания следует, что на стенках микроканала 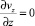и τnn = –p. Поэтому р является давлением газа на стенку. В соответствии с формулой (4) на стенках микроканала имеет место равенство

p = P(z), (5)

из которого следует, что давления газа на поверхности микроканала зависят только от продольной координаты z и одинаковы во всех точках контуров H(x, y) = 0, являющихся границами поперечных сечений микроканала плоскостями z = const. Для того чтобы давление газа р внутри потока не зависело от поперченных координат, необходимо, чтобы выполнялось равенство

λ = –μ. (6)

В этом случае равенство p = P(z) выполняется в любых точках потока. При этом из последнего уравнения системы (3) следует вид компоненты скорости vz и ее производной по z

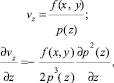(7)

где функция f(x, y) подлежит определению.

При выполнении условия (6) третье уравнение системы (3) принимает вид

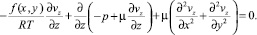
С учетом формул (7) последнее равенство преобразуется к виду

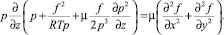(8)

К сожалению, полученное равенство никогда не может быть выполнено точно, так как его правая часть зависит только от двух координат, а левая – от всех трех пространственных координат. Следовательно, строго одномерные установившиеся изотермические течения вязких газов не существуют, а квазиодномерные течения вязкого газа могут быть изучены на основе линеаризации уравнения (8).

Допуская справедливость утверждения 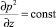, уравнение (8) можно представить в таком виде

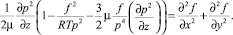(9)

В случаях, когда выполняется неравенство

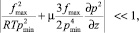(10)

уравнение (9) можно заменить приближенным уравнением

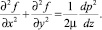(11)

Так как в полученном уравнении левая часть зависит от координат x и y, а правая является функцией только координаты z, то должна иметь место система равенств

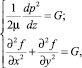(12)

где G – постоянная величина, подлежащая определению.

Если при z = z1 p = p1 и при z = z2 p = p2, то можно найти

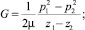
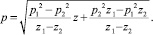(13)

При этом функция f(x, y) находится в результате решения краевой задачи

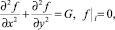(14)

где l – контур поперечного сечения микроканала.

В случаях, когда λ ≠ –μ, давление в потоках газа в микроканалах должно быть функцией не только продольной, но и поперечных координат, и здесь равенство (5) следует рассматривать только как приближенное, принимая 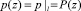. Для определения полей давлений и скоростей в потоке газа в микроканалах при условии выполнении неравенства (10) можно использовать уравнение (11).

Для решения задачи (14) удобно перейти к безразмерным величинам

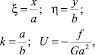(15)

где a и b ‒ характерные размеры вдоль координатных осей поперечного сечения микроканала. При этом краевая задача (14) преобразуется к виду

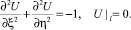(16)

После определения функции U можно вычислить массовый расход газа Q, протекающего через микроканал в единицу времени, используя формулу

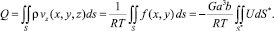(17)

В связи с переходом к безразмерным величинам условие приемлемости получаемых решений (10) преобразуется к виду

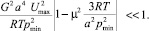(18)

Аналогичные задачи ранее решались для ламинарных потоков несжимаемой вязкой жидкости в трубах различных сечений [2]. В отличие от газов течения вязких жидкостей могут быть теоретически строго одномерными. Для потоков жидкостей можно принять

vz = f(x, y);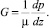

При этом в переменных (15) задача для определения функции U сводится к задаче (16), а формула для определения массового расхода жидкости через трубу принимает вид

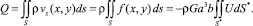
Для труб c круглыми, эллиптическими и в виде правильных треугольников сечениями в книге [2] представлены простые точные решения задачи (14) с использованием полиномов, описывающих вид границ сечений, и алгебраические формулы для расчетов расходов Q. Для труб прямоугольного сечения точное решение задачи (14) представлено в рядах, а для расчета расходов предложена таблица. Эти формулы достаточно просто обобщаются на случаи течений газов в микроканалах соответствующих сечений. Для потоков газа в микроканалах при выполнении условия (18) справедливы следующие формулы:

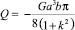(эллиптическое сечение, a ≥ b, a и b – полуоси),

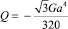(сечение – правильный треугольник со стороной 2a),

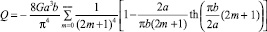(прямоугольное сечение 2a×2b),

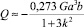(полуэллиптическое сечение (–a ≤ x ≤ a, 0 ≤ y ≤ b)).

Последняя формула дает приближенные значения расходов с погрешностью до 5 % при k < 10. При k > 10 целесообразно использовать формулы для определения расходов газа в широких щелях [4] или численные методы решения задачи (16) и вычисления интеграла (17) для всех k.

Рецензенты:

Потетюнко Э.Н., д.ф.-м.н., профессор кафедры теории упругости факультета математики, механики и компьютерных наук, ФГАОУ ВПО «Южный федеральный университет» Министерства науки и образования РФ, г. Ростов-на-Дону;

Сметанин Б.И., д.т.н., доцент, профессор кафедры теоретической и компьютерной гидроаэродинамики факультета математики, механики и компьютерных наук, ФГАОУ ВПО «Южный федеральный университет» Министерства науки и образования РФ, г. Ростов-на-Дону.

Работа поступила в редакцию 01.08.2013.

Библиографическая ссылка