Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Жгун Т.В. 1

---

1 ГОУ ВПО «Новгородский государственный университет имени Ярослава Мудрого»

В статье предложена методика построения интегральной характеристики динамической системы с помощью метода главных компонент на основе измеряемых данных. Показано, что при изменении входных данных все главные факторы определяются разными переменными и применение метода главных компонент при вычислении интегральной характеристики не позволяет произвести корректное сравнение показателей объектов. Рассматривая статистические данные с точки зрения теории обработки сигналов как сигнал, в котором имеется полезная информация – слабый сигнал, который нужно выделить, и шум, и предполагая, что изменение входных данных может иметь как случайную природу (шум), так и неслучайную (сигнал), будем считать, что именно неслучайные коэффициенты главных компонент и являются той характеристикой системы, которая позволит нам определить веса интегрального индикатора и, значит, качество системы на промежутке наблюдений при изменении входных данных. Наличием неслучайного (т.е. значимого) вклада переменной в структуру главных компонент будем считать не большую величину факторной нагрузки, а инвариантность факторной нагрузки при возмущениях, признаком которой будет величина отношения сигнал/шум. Приводится апробация методики на примере вычисления интегральной оценки демографического развития на основе данных государственной статистики для муниципальных образований Новгородской области. Предлагаемая методика может быть использована для вычисления интегральных оценок качества любой динамической системы.

Статья в формате PDF

393 KB

региональная демографическая политика

демографические характеристики

мониторинг системы показателей

метод главных компонент

качество системы управления

система показателей эффективности

1. Айвазян С. А. Интегральные индикаторы качества жизни населения: их построение и использование в социально-экономическом управлении межрегиональных сопоставлениях. – М.: ЦЭМИ РАН, 2000. – 56 с.

2. Загоруйко Н.Г. Прикладные методы анализа данных и знаний. – Новосибирск: Изд-во Института математики, 1999. – 270 с.

3. Кузнецов М.П., Стрижов В.В. Построение интегрального индикатора с использованием ранговой матрицы описаний // Интеллектуализация обработки информации: доклады 9-й международной конференции, 2012. – С. 130–132.

4. Мельников Д.И., Стрижов В.В., Андреева Е.Ю., Эдензартер Г. Выбор опорного множества при построении устойчивых интегральных индикаторов // Математические методы распознавания образов. 14-я Всероссийской конференция ММРО-14: сборник докладов. – МАКС~Пресс, 2009. – С. 159–162.

5. Рыбаковский В.В. Интегральная оценка демографического неблагополучия регионов России. (Методологические вопросы) // Социальная политика и социальное партнерство. – 2008. – № 6 http://rybakovsky.ru/stati1a6.html.

Проблемы демографического развития страны в последнее время стали позиционироваться как наиболее существенные для поступательного развития России. Демографические процессы, которые недавно были особо значимыми лишь для специалистов, в настоящее время выдвинулись в центр общественного внимания. Государством в последние годы предпринимаются меры, направленные на изменение негативных демографических процессов.

Для реализации государственной демографической политики необходимо своевременное реагирование на демографические тенденции в текущий период. Обеспечение своевременного реагирования немыслимо без учета региональных и территориальных особенностей демографического развития, для которого необходима организация системы мониторинга демографической ситуации в Российской Федерации и ее субъектах, а также создание необходимых инструментов такого мониторинга. Объективное определение характеристик демографического развития является обязательным инструментом такого мониторинга. Целью работы является создание инструмента мониторинга демографической ситуации в Российской Федерации – методика объективного определения характеристик демографического развития.

Традиционно демографическая ситуация характеризуется по трем основным параметрам: рождаемости, смертности и миграции. Но при всей важности и необходимости использования отдельных показателей, они не могут обеспечить адекватное сравнение разных территорий. Трудности сравнения между собой регионов по характеру демографической ситуации не только в ограниченных возможностях использования для этого тех или иных показателей. Часто противоположная направленность динамики различных показателей в разных регионах не позволяет однозначно оценивать ситуацию. Так, в Москве в 2005 г. суммарный коэффициент рождаемости составлял 1,140, а ожидаемая продолжительность жизни – 71,36 года, тогда как в Эвенкийском автономном округе соответственно 2,261 и 57,56. Очевидно, что когда уровни и динамика демографических показателей различны, невозможно произвести сравнение территорий [5]. Следовательно, для выбора основных точек управленческого воздействия необходим анализ демографической динамики в целом.

По мнению С.А. Айвазяна, интегральный индикатор той или иной синтетической категории качества представляет собой «свертку» оценок более частных свойств и критериев этого понятия: статистических показателей либо экспертных оценок [1]. Отметим, что применение экспертных оценок наряду с субъективностью имеет ещё один недостаток: не для всех оцениваемых систем можно найти достаточное количество квалифицированных экспертов. В частности, такова и рассматриваемая проблема: экспертов, одинаково хорошо разбирающихся в тонкостях демографической ситуации в различных муниципальных образований, видимо, не существует вообще. Следовательно, использование статистических данных остаётся единственно возможным. Необходимо отметить, что при формировании структуры интегрального показателя и его расчете возникают серьезные затруднения, связанные с субъективностью выбора первичной информации, с достоверностью и репрезентативностью статистической информации и с методической неопределенностью определения значения интегрального показателя [1, 3, 4]. Отметим, что переменные, значения которых можно измерять только статистически, имеют для исследуемой ситуации достаточно условный характер, лишь опосредованно отражая внутреннюю структуру рассматриваемой интегральной характеристики.

Рассмотрим построение интегральной оценки системы из m объектов, для которой в моменты времени t = t1, t = t, ..., t = tk известны таблицы описаний этих объектов размерностью m×n – матрицы 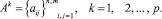Для каждого момента t = tk вектор интегральных показателей будет иметь вид

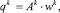(1)

где 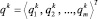– вектор интегральных индикаторов; 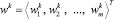– вектор весов показателей для момента .Для фиксированного момента t = tk интегральную оценку чаще всего записывают для каждого рассматриваемого объекта c номером i в виде аддитивной свертки данных с некоторыми весами

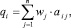i = 1, 2, … m. (2)

Обычно веса wj назначаются экспертами. Метод экспертных оценок широко используется в силу простоты получения информации, но не может считаться объективным. Лишены субъективности формальные методы, в частности, широко используется метод главных компонент, предложенный С.А. Айвазяном [1]. Согласно [1], вектор интегральных индикаторов для каждого объекта q = A∙w1 есть проекция векторов-строк матрицы данных A на первую главную компоненту, w1– собственный вектор, соответствующий максимальному собственному значению ковариационной матрицы .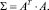

Этот метод используется для оценки статических систем в случае, если первая главная компонента хорошо приближает моделируемую ситуацию, т.е. в случае, если максимальное собственное число ковариационной матрицы дает вклад не менее 70 % в сумму всех собственных чисел. Однако если такое предположение не выполняется, проекцию на первую компоненту нельзя считать удачной оценкой. Ситуацию можно исправить, если вместо одной компоненты выбрать l компонент, чтобы относительная доля разброса γl, приходящаяся на первые l (l ≤ n) l ( главных компонент):

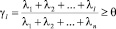, (3)

была не менее определенной величины. Мы будем рассматривать далее случай, когда θ = 0,75. Выбрав главные компоненты, в случае, когда результаты применения метода главных компонент (или метода факторного анализа) устраивают исследователя, для каждого признака эффект воздействия выбранных факторов суммируем и таким образом определяем веса в (2). Критерием удовлетворительного решения обычно является возможность четкой содержательной интерпретации получившихся факторов. Метод главных компонент формально не требует использования вращений, так как предлагает единственное решение; но в практике обычно используется вращение варимакс для облегчения интерпретации компонент, который приводит к увеличению больших и уменьшению малых значений факторных нагрузок.

Рассмотрим статистические данные, предоставленные Комитетом государственной статистики Великого Новгорода, отражающие демографическую ситуацию в муниципальных образованиях Новгородской области. Среди имеющихся данных была устранена мультиколлинеарность и рассматривались 9 переменных: коэффициент рождаемости; коэффициент смертности; коэффициент младенческой смертности; коэффициент брачности; коэффициент разводимости; коэффициент миграции; доля населения моложе трудоспособного возраста; доля населения старше трудоспособного возраста; доля мужчин среди населения. В табл. 1 приведены результаты факторного анализа данных, относящихся к различным моментам наблюдения.

Интегральная оценка вычисляется на основании нормированных данных (т.е. все значения приведены на интервал [0, 1] и соответствуют принципу «чем больше, тем лучше»: большему значению показателя (при прочих равных) соответствует большее значение интегрального индикатора). Предполагается, что в данных нет объектов-выбросов и пропущенных значений [2]. Для вычисления главных компонент выполнено центрирование, после которого данные имеют нулевое среднее и единичное среднеквадратичное отклонение. Данные были обработаны с помощью пакета SPSS Statistics версии 11.0 и для каждого года построены главные факторы. Крестиками отмечены значимые переменные – те, у которых абсолютное значение факторной нагрузки не менее 0,6.

Таблица 1

Результаты факторного анализа

Значимые переменные для всех факторов разных лет сильно отличаются. Значит, невозможно верно выделить значимые (определяющие ситуацию) переменные для этих факторов для всей совокупности данных, в то время как анализ данных любого года в отдельности позволяет это сделать. Чтобы иметь возможность оценивать характеристики системы в динамике, посмотрим на получаемую при работе информацию с точки зрения теории обработки сигналов как на сигнал, в котором имеется полезная информация – слабый сигнал, который нужно выделить, и шум. Измерение переменных неизбежно связано с точностью измерительного прибора, поэтому любой полученный с помощью измерения результат неизбежно содержит ошибку измеряемых данных, которая носит случайный характер. Статистические данные ‒ тоже результат измерения, неизбежно содержащего погрешность измерения. Любой результат, полученный на основании этих данных, также будет содержать эту неустранимую ошибку. Переход к другому моменту времени означает изменение данных, которое вызвано как изменением объясняющих переменных, так и изменением случайной составляющей. Весовые коэффициенты при построении интегрального показателя будут иметь совсем иные значения для следующего момента наблюдений. Причем изменение этих значений может быть вызвано как изменением входных данных, так и случайными ошибками. Предполагая непрерывную зависимость вычисляемого показателя от изменения входных данных, определим природу такого изменения.

Будем считать, что именно истинные коэффициенты главных компонент и являются той характеристикой системы, которая позволит нам определить веса интегрального индикатора и, значит, качество системы на промежутке наблюдений. Наличием неслучайного (т.е. значимого) вклада переменной в структуру главных компонент будем считать не большую величину факторной нагрузки, а инвариантность факторной нагрузки при возмущениях, признаком которой будет величина отношения сигнал/шум. По статистическим данным для ряда наблюдений определим веса факторных нагрузок для l первых (наиболее весомых) главных компонент и определим значение интегрального показателя для фиксированного момента времени t = tk. по формуле

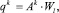(4)

где 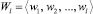– матрица, составленная по первым l компонентам с использованием всех наблюдений с учетом (3).

Применим изложенную методику для вычисления интегральной оценки демографического развития муниципальных образований Новгородской области. В табл. 2 представлено определение неслучайных коэффициентов факторных нагрузок для второго фактора. В последней строке отмечены те переменные, где факторную нагрузку можно считать неслучайной – переменные, где отношение сигнал/шум более чем 2,2. Такая величина применяется в технике при выделении сигнала из сильно зашумленных данных. Этому условию отвечают переменные 4, 5 (коэффициенты брачности и рождаемости) и переменные 6 (коэффициент миграции) и 9 (доля мужчин). Направление собственных векторов выбираем, чтобы максимизировать услышанный сигнал, т.е. сумму ОСШ у действующих переменных.

Таблица 2

Коэффициенты факторных нагрузок для второго фактора

Значения весовых коэффициентов переменных, полученные по 4 главным компонентам с учетом выбора направлений компонент, максимизирующего целевую функцию с и соответствующей нормировки на корень из собственных чисел, согласно (3), приведены в табл. 3.

Демографические данные ‒ это, пожалуй, единственный вид статистических данных, для которых значение интегральной оценки ожидаемо. Очевидно, что в любом субъекте России налицо одна и та же ситуация: на фоне некоторого общего улучшения демографической ситуации в рассматриваемый период имеется неравномерность положения в регионе. Центр является «пылесосом», выкачивающим из глубинки молодое активное население, из-за чего положение в центре самое лучшее, а дальние районы представляют «кольцо смерти», окружающее благополучный центр. Ближайшие к центру районы и районы с развитой промышленностью занимают промежуточное положение между благополучным центром и неблагополучными окраинами. Именно такую картину и дают нам вычисленные значения интегрального показателя. Изменение значения интегрального показателя по годам для некоторых районов Новгородской области можно увидеть на рисунке. Близкие к центру районы (Старорусский) и районы с развитой промышленностью (Парфинский) занимают промежуточное положение между Великим Новгородом и отдаленными районами (Батецкий район).

Таблица 3

Суммарные значения весовых коэффициентов

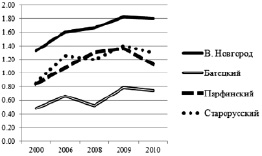
График изменения демографической интегральной характеристики

Характеристики демографической ситуации той или иной территории дают лишь интегральное представление о характере демографических процессов, причем лишь на фоне общей совокупности рассматриваемых территорий. Они показывают, где совокупно демографические показатели хуже, а где лучше относительно некоторого общего среднего, которым может быть и средний индекс по региону, и его медианное значение. Вычисление интегральных оценок демографического развития не исключает необходимости тщательного анализа всех его составных элементов и поиска путей их улучшения.

Заключение

Предлагаемая методика может быть использована при организации реализации государственной демографической политики в территориальных образованиях Российской Федерации любого уровня, для построения интегральной оценки социально-экономического развития и для вычисления интегральных оценок изменения качества любой системы.

Рецензенты:

Пиковский А.А., д.э.н., профессор кафедры прикладной экономики Новгородского государственного университета имени Ярослава Мудрого, г. Великий Новгород;

Кирьянов Б.Ф., д.т.н., профессор кафедры прикладной математики и информатики Новгородского государственного университета имени Ярослава Мудрого, г. Великий Новгород.

Работа поступила в редакцию 19.07.2013.

Библиографическая ссылка