Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Соколова Е.А. 1

---

1 ФГБОУ ВПО «Северо-Кавказский горно-металлургический институт (Государственный технологический университет)»

При разработке аппаратно-программного комплекса музеев и картинных галерей стояла задача определить оптимальный подбор экспонатов. Для реализации поставленной задачи рассматривается теоретико-множественный подход. Теоретико-множественный подход предполагает анализ множеств информационных сообщений, объектов и т.п. с точки зрения их количественных признаков. Содержание поиска качественного аспекта информации заключается в том, чтобы выделять, изучать и исследовать характеристики множества сообщений в связи с качественными моментами составляющих его частей. Одним из путей решения задачи по превращению потенциальной информации в информацию актуальную является использование наиболее рациональных средств кодирования (декодирования) информации. В статье описана формальная постановка для решения поставленной задачи, алгоритм поиска и рассмотрен пример решения задачи поиска необходимого контента по атрибутам и ключевым словам.

Статья в формате PDF

430 KB

теоретико-множественный подход

множество информационных сообщений

контент

1. Знаменский А.В., Черкалин С.Д. Компьютер в экспозиции. Взгляд из провинции. // Музеи и информационное пространство: проблема информатизации и культурное наследие. Тезисы докладов. Пятая ежегодная конференция АДИТ-2001. – Тула, 2001. – С. 15–16.

2. Соколова Е.А., Гречаный С.В.Оптимизация алгоритма компрессии видеоизображений вариабельными фрагментами // Устойчивое развитие горных территорий. – 2011. – № 4(10). – 5 с.

3. Соколова Е.А., Мирошников А.С. Разработка программных продуктов для конвертации мультимедийных изображений // Перспективы науки. – 2012. – № 11(38).

4. Черненко В.В. Использование автоматизированных информационных систем в экспозиции – с. 88 Музеи Москвы и музеология XX века: Тезисы научной конференции (М., 25–26 ноября 1997 г.) // отв. ред. Ю.У. Гуральник – М.: РГГУ, 1997.

5. Эльзассер М.Э. Князева Н.А. Новое измерение партнерства: виртуальная выставка и реальное сотрудничество // Электронный потенциал музея: стимулы и ограничения, достижения и проблемы: тезисы докладов XXX Международной конференции CIDOC-АДИТ-2003. – СПб., 2003. – С. 55–56.

При разработке аппаратно-программного комплекса музеев и картинных галерей стояла задача реализовать оптимальный подбор экспонатов. Разработанные программные средства должны поддерживать поиск необходимого контента по атрибутам и ключевым словам.

Для решения этой задачи был использован теоретико-множественный подход.

Теоретико-множественный подход

Теоретико-множественный подход предполагает анализ множеств информационных сообщений, объектов и т.п. с точки зрения их количественных признаков. Здесь не происходит полного отмежевания от качества исследуемых информационных объектов и их элементов. Напротив, уже само исследование формализованных множеств, сообщений (например, данных судебной статистики и др.) постоянно предполагает наличие каких-либо качественных моментов, признаков, позволяющих говорить о содержании исследуемых информационных сообщений. Содержание поиска качественного аспекта информации заключается в том, чтобы выделять, изучать и исследовать характеристики множества сообщений в связи с качественными моментами составляющих его частей.

Одним из путей решения задачи по превращению потенциальной информации в информацию актуальную является использование наиболее рациональных средств кодирования (декодирования) информации (например, определение в цифровом коде ЕГРПОУ информации о предприятии или выражение текста закона в условных символах специального информационно-поискового языка).

Формальная постановка задачи

Для обозначения эффективного алгоритма поиска оптимальных экспонатов выставочного центра в ответ на запрос пользователя удобно использовать теоретико-множественный подход. Исследуемые объекты представим в виде множества их свойств, которые определены для оценки в процессе поиска:

O = {p} = {p0, p1, …, pn} (1)

где O – исследуемый объект; p – свойство, которое участвует в поиске.

Приоритетность свойств при поиске и оценке релевантности отображается в виде множества весовых коэффициентов, которые определяются путем экспертного анализа исследуемого объекта (в данном случае ‒ экспоната выставки).

{k} = {k0, k1, …, kn}. (2)

Поисковый запрос соответственно теоретико-множественному подходу удобно представить как множество слов. Кроме того, для повышения эффективности и точности поиска, а также для обеспечения высокой достоверности результатов из множества слов поискового запроса удаляются все повторения и семантически «слабые» конструкции (например, союзы и предлоги).

R = {w, ∀w(Fsem(w) ≠ ∅)}, (3)

где R – поисковый запрос; w – слово в запросе; Fsem(w) – функция определения семантических соответствий для слова.

Функция определения соответствия свойства исследуемого объекта слову из запроса определяется как произведение соответствующего весового коэффициента и показателя оценочной функции вхождения слова в значение свойства:

Feval(p, w) = kp∙Fex(p, w), (4)

где p – свойство объекта; w – слово в запросе; kp – весовой коэффициент для свойства; Fex – оценочная функция встречаемости слова в значении свойства.

Оценочная функция встречаемости слова зависит от способа интерпретации значения свойства и целей поиска. Например, для атрибута «Автор произведения» сущности «Экспонат» оценочная функция встречаемости слова может быть определена системой следующего вида:

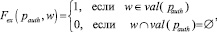(5)

где pauth – свойство «Автор произведения»; w – слово поискового запроса; val(pauth) – множество значений свойства «Автор произведения» для каждого объекта.

Используя представление (1) и функцию (4), интегральный показатель соответствия исследуемого объекта поисковому запросу (релевантность) определяем как среднее арифметическое суммы показателей функции (4):

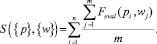(6)

Результаты оценки релевантности для соответствующих объектов и сами исследуемые объекты представляются в виде множества, элементы которого сортируются по убыванию уровня релевантности.

Алгоритм поиска

1. Даны множества свойств объектов O = {p} = {p0, p1, …, pn} и множества весовых коэффициентов {k} = {k0, k1, …, kn}, определяющих приоритетность свойств.

2. Вводим в строку поиска запрос R, включающий в себя слова wi ().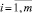

3. Определяем соответствие свойства исследуемого объекта слову из запроса по формуле

Feval(p, w) = kp∙Fex(p, w),

где Feval(p, w) = kp∙Fex(p, w) равно 1, если слово входит в свойство, 0 в противном случае.

4. Определяем среднее арифметическое суммы показателей функции Feval(p, w) = kp∙Fex(p, w)

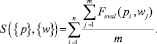
5. Сортируем объекты в порядке убывания уровня релевантности, определенного на шаге 4.

6. Вывод объектов.

Пример решения задачи поиска необходимого контента по атрибутам и ключевым словам

Дана табл. 1, содержащая некоторое количество экспонатов.

Шаг 1.

Задаем множество свойств для оценки в процессе поиска

O = {p} = {p0, p1, …, pn}, (1)

где O – каждый исследуемый объект; p – свойство, которое участвует в поиске; p1 – название; p2 – автор; p3 – год создания; p4 – описание; p5 – категория.

O = {p} = {название, автор, год создания, описание, категория}.

Таблица 1

Экспонаты

Приоритетность свойств при поиске и оценке релевантности отображаем в виде множества весовых коэффициентов

{k} = {k0, k1, …, kn};

{k} = {1; 1; 0,2; 0,2; 0,2}

Шаг 2.

Введем исходный поисковый запрос, включающий в себя строку «Мона Лиза».

Шаг 3.

Определим уровень релевантности для первого объекта:

Feval(p1, «Мона») = 0;

Feval(p2, «Мона») = 0;

Feval(p3, «Мона») = 0;

Feval(p4, «Мона») = 0;

Feval(p5, «Мона») = 0;

Feval(p1, «Лиза») = 0;

Feval(p2, «Лиза») = 0;

Feval(p3, «Лиза») = 0;

Feval(p4, «Лиза») = 0;

Feval(p5, «Лиза») = 0;

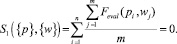
Данный результат не будет отображен в результатах поиска.

Шаг 4.

Определим уровень релевантности для второго объекта:

Feval(p1, «Мона») = 0;

Feval(p2, «Мона») = 0;

Feval(p3, «Мона») = 0;

Feval(p4, «Мона») = 0.2;

Feval(p5, «Мона») = 0;

Feval(p1, «Лиза») = 0;

Feval(p2, «Лиза») = 0;

Feval(p3, «Лиза») = 0;

Feval(p4, «Лиза») = 0.2;

Feval(p5, «Лиза») = 0;

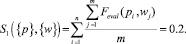
Данный результат войдет в список отображаемых результатов поиска.

Шаг 5.

Определим уровень релевантности для третьего объекта:

Feval(p1, «Мона») = 1;

Feval(p2, «Мона») = 0;

Feval(p3, «Мона») = 0;

Feval(p4, «Мона») = 0;

Feval(p5, «Мона») = 0;

Feval(p1, «Лиза») = 1;

Feval(p2, «Лиза») = 0;

Feval(p3, «Лиза») = 0;

Feval(p4, «Лиза») = 0;

Feval(p5, «Лиза») = 0;

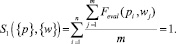
Данный результат в список отображаемых результатов поиска.

Шаг 6.

Определим уровень релевантности для четвертого объекта:

Feval(p1, «Мона») = 0;

Feval(p2, «Мона») = 0;

Feval(p3, «Мона») = 0;

Feval(p4, «Мона») = 0;

Feval(p5, «Мона») = 0;

Feval(p1, «Лиза») = 0;

Feval(p2, «Лиза») = 0;

Feval(p3, «Лиза») = 0;

Feval(p4, «Лиза») = 0;

Feval(p5, «Лиза») = 0;

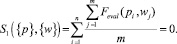
Данный экспонат не войдет в список отображаемых результатов поиска.

Шаг 7.

Результат поиска (табл. 2).

Таблица 2

Результаты поиска

Критическое обсуждение результатов

В результате разработки аппаратно-программного комплекса музеев и картинных галерей был реализован оптимальный подбор экспонатов с использованием теоретико-множественного подхода. Разработанные программные средства поддерживают поиск необходимого контента по атрибутам и ключевым словам.

Рецензенты:

Петров Ю.С., д.т.н., профессор, зав. кафедрой «Теоретические основы электротехники», ФГБОУ ВПО «Северо-Кавказский горно-металлургический институт (Государственный технологический университет)», г. Владикавказ;

Гроппен В.О., д.т.н., профессор, зав. кафедрой «Автоматизированная обработка информации», ФГБОУ ВПО «Северо-Кавказский горно-металлургический институт (Государственный технологический университет)», г. Владикавказ.

Работа поступила в редакцию 19.07.2013.

Библиографическая ссылка