Мехатронные ударные системы (УМС) используются в горнодобывающей, горно-перерабатывающей, строительной промышленности и в других отраслях, имеющих важное народнохозяйственное значение [1, 2].
Важнейшей задачей создания УМС (молотов) является обеспечение наивысшей мощности удара без обратного воздействия на базовую машину (трактор, экскаватор, танк и др.). Обычно создание УМС рассматривается как задача механики без учета управляющей подсистемы [3–6]. Сложные механические системы ударного действия относятся к классу мехатронных систем, то есть механических систем с динамическим управлением, основанным на преобразовании информации о состоянии процессов в энергетических каналах всей УМС. Поэтому анализ динамических процессов в сложных механических системах только с позиций теории механизмов и машин является недостаточным, так как не отображает информационных процессов.
Структурные моделимехатронных систем
При анализе сложных систем, к которым относится УМС, на сегодняшний день используется двухблочная модель В.М. Глушкова (рис. 1) в виде объекта управления (ОУ – операционное устройство) и управляющего автомата (УА). В этой модели особый акцент сделан на управление, тогда как вся основная часть (ОУ) рассматривается как своего рода «черный ящик», для которого известен алгоритм управления.
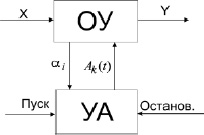
Рис. 1. Структурная модель В.М. Глушкова
Рассмотрим УМС с позиции системной модели Ю.Ф. Мухопада [7] в виде полного пятивершинного графа (рис. 2).
Как модель В.М. Глушкова, так и модель Ю.Ф. Мухопада создавались для отображения и преобразования информационных процессов в системе. При этом множество входных сигналов X и множество выходных сигналов Y есть информационные характеристики объекта управления (ОУ).
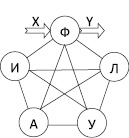
Рис. 2. Структурная модель Ю.Ф. Мухопада
Для модели дискретных систем у В.М. Глушкова X есть двоичный код x1, x2, ... xm, а Y – аналогично y1, y2, ... ym. В частном случае m = n для электронных вычислительных машин. В системной модели Ю.Ф. Мухопада сигналы X и Y могут быть как цифровыми, так и аналоговыми; при этом Ф – функциональная, И – информационная, Л – логическая, А – адресная, У – управляющая подсистемы.
Для УМС характерно наличие двух каналов – непосредственно энергетического канала, преобразующего энергию входного импульса X в энергию, передающуюся инструменту для удара Y, и информационного канала, отображающего «рождение» информации (через датчики α1, α2, ..., αq) о процессах в энергетическом канале и канала преобразования информации с целью выборки команд управления энергетическим каналом. При этом по структурной модели функциональная подсистема – есть комплекс механизмов и устройств энергетического канала, исполняющих свои функции под действием управляющих команд A1, A2, ..., Ak для включения и отключения пневмо- и гидродвигателей с целью перемещения главных механических подсистем, содержащих ударный инструмент. Входными сигналами для системы управления являются показания датчиков движения и положения α1, α2, ..., αq, а выходными – команды A1(t), A2(t), ..., Ak(t) (рис. 3).
На рис. 3 обозначены: ЭЗУ – энергетическое запоминающее устройство (в виде пружины), S1, S2, ..., Sm – пневмо- или гидросистема, α1, α2, ..., αq – датчики информации о процессах в энергетической системе, A1, A2, ..., Ak – команды управления, X – энергетический канал входного воздействия (пневмо или гидропровод), УР – уровень размещения мехатронной ударной системы (Земля), ЭК – энергетический канал, K1, K2, ..., Ki – каналы ответвления с клапанами соответственно Д1, Д2, ..., Дk. Сигнал Y пропорционален выходной энергетической мощности единичного удара, сообщенной снаряду С.
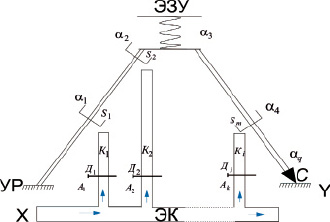
Рис. 3. Схематическая модель мехатронной ударной системы
Рассматривая управляющую подсистему как автомат с правилом функционирования Мура, его структуру можно представить по новой оригинальной схеме [8–11] в виде рис. 4.
В оригинальных конструкциях УМС [1–6] в энергетическом канале имеется своего рода информационная подсистема в виде устройств, обеспечивающих сохранение энергии. Это энергетическое «запоминающее» устройство (ЭЗУ) отображено на схеме (см. рис. 3) в виде условной пружины, которая может быть реализована механическими, гидравлическими и пневматическими средствами. Адресная подсистема в энергетическом канале представлена системой непосредственных связей механизмов передачи энергии.
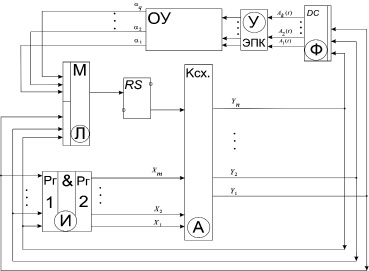
Рис. 4. Автомат управления мехатронными ударными системами
В информационном канале УМС информационная подсистема есть набор блоков (регистры памяти Рг 1 и Рг 2), хранящих код состояния процессов в энергетических каналах.
Управляющая подсистема всей УМС есть автомат выработки последовательности команд в логической и временной взаимосвязи. Поэтому состояния системы УМС отображаются соответствующими состояниями α(t) автомата управления (см. рис. 4) в момент t. Код α(t) обозначен в виде x1, x2, ..., xm. Этот код хранится в регистре (Рг 2), а в следующий момент времени (t + 1) код состояния α(t + 1)в виде y1, y2, ..., ym хранится в регистре Рг 1. Эта информация (y1, y2, ..., ym) расшифровывается, т.е. преобразуется в унитарный код дешифратором (DC) для выдачи команд A1(t), A2(t), ..., Ak(t). Естественно, что команды Ak(t), не имеющие достаточного энергетического уровня в виде информационных сигналов логической «1» (включить) и логического «0» (отключить), необходимо усилить.
Логическая подсистема (Л) в управляющем автомате представлена комплексом датчиков информации α1, α2, ..., αq, размещенных на механизмах энергетического канала (ОУ) и мультиплексором (М) с RS триггером. Мультиплексор по коду y1, y2, ..., ym производит выбор единственного логического условия от датчика αq из всего множества α1, α2, ..., αq (αq ∈ {α}) для преобразования конкатенации кодов αq x1 x2 ... xm ... адресной (А) подсистемы в код выходной команды Ak(t), совпадающей с состоянием α(t) автомата управления. Следует заметить, что, согласно структуре автомата (см. рис. 4), выбирается только то условие, которое соответствует состоянию процесса в энергетическойподсистеме.
Роль адресной подсистемы в автомате управления выполняет комбинационная схема (Ксх.), которая чаще всего заменяется постоянным запоминающим устройством (ПЗУ) или программируемой логической схемой (ПЛМ). В адресной подсистеме (А) хранятся в ПЗУ коды состояний (или их аналог в виде логических комбинаций в ПЛМ) и их переходов из одного состояния механической подсистемы в другое состояние в процессе преобразования энергетических импульсов.
Математические модели мехатронных систем
Правило преобразования состояний α(t) → α(t + 1) может быть получено, если отобразить процессы в энергетическом канале в виде динамических переходов с проверкой значения логических условий αq, соответствующих предыдущему состоянию α(t), и с выработкой значения нового логического условия, соответствующего α(t + 1).
Математической моделью, способной наилучшим образом отразить динамические преобразования α(t) → α(t + 1) с учетом αq ∈ {α}, является сеть Петри. Правила составления сети Петри для сложных механических систем, к которой относятся системы ударного действия с запоминанием (хранением) энергетического потенциала, требуют самостоятельного подхода, который изложен в работе [7, 8, 12].
Для реализации задачи управления и контроля рассмотрим УМС в виде молота с переменной массой ударника (рис. 5). Процесс ударного разрушения горных пород состоит из нескольких этапов движения в течение одного цикла работы (взвод, сохранение энергии, разгон, удар, движение внутри породы, возвращение подвижных частей в исходное положение).
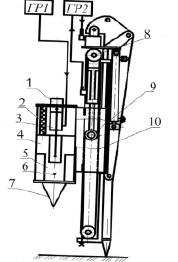
Рис. 5. Конструктивная схема молота с переменной массой ударника
На рис. 5 обозначено: 1 – первый двигатель, 2 – пружина аккумулятора, 3 – захват, 4 – корпус ударника со встроенными датчиками свободности/занятости снарядом D1 и D3 в области захвата и в основании (в области ударной части снаряда), 5 – ударная часть снаряда, 6 – болванка (дополнительный снаряд), 7 – инструмент, 8 – мультипликатор механический со встроенными датчиками свободности/занятости ударником D2 и D4 на уровне крайней точки возведенного корпуса ударника и на уровне крайней точки до взвода корпуса ударника, 9 – шток второго гидродвигателя, 10 – молот.
УМС с переменной массой ударника работает следующим образом: масляный гидронасос, вращаемый двигателем базовой машины, через гидрораспределитель ГР1 воздействует на первый гидродвигатель 1 и захват 3, соединяя захват с инструментом 7. Затем этот же поток масла взводит снаряд и натягивает пружину аккумулятора 2. Наряду с этим процессом масляный гидронасос воздействует через ГР2 на второй гидродвигатель 9, который соединяется с мультипликатором 8, что приводит к взводу ударника 4 над обрабатываемой поверхностью. Далее масло удаляется из поршневой полости второго гидродвигателя и нагнетает его в штоковую полость, что приводит к освобождению ударника. Происходит разгон ударника, а за ним после достижения ударником обрабатываемой поверхности происходит разгон снаряда в ударнике. Затем происходит удар по поверхности монолитного блока горной породы ударной частью снаряда 5. Под действием дополнительного снаряда 6 со встроенной пружиной происходит дополнительный удар сразу после основного удара. И в завершении производится возврат подвижных частей системы в исходное состояние.
Для обеспечения управления и контроля таких ударных систем необходимо исследовать сетевую математическую модель (сеть Петри). Рассмотрим сеть Петри УМС (см. рис. 6) и ее списки условий и событий, приведенные в табл. 1 и 2. Список предусловий и постусловий приведен в табл. 3.
Полученная сетевая модель должна обладать следующими свойствами:
1. Безопасность сети при подаче любых внешних воздействий. Нарушения безопасности могут свидетельствовать об ошибке на стадии логического проектировании подсистем управления и контроля.
2. Живость переходов. Отсутствие живости переходов определяется программной или аппаратной избыточностью сети МПС или ошибкой проектирования.
3. Достижимость. Сетевая модель должна иметь не только начальную разметку, но и некоторое непустое множество всех допустимых разметок.
4. Отсутствие тупиков. Наличие тупика означает принудительную остановку снаряда на одном из этапов работы УМС.
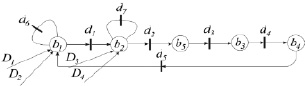
Рис. 6. Сеть Петри УМС
Таблица 1
Список условий
|
Обозначение |
Условия |
Наличие начальных условий |
|
b1 |
Принят запрос с датчика D1, D3 |
Есть |
|
b2 |
Принят запрос с датчика D2, D4 |
Есть |
|
b3 |
Выполнение удара системой |
Нет |
|
b4 |
Возврат системы к исходному состоянию |
Нет |
|
b5 |
Сохранение энергии |
Нет |
Таблица 2
Список событий
|
Обозначение |
События |
|
d1 |
Переход от взвода к разгону |
|
d2 |
Переход от разгона к сохранению энергии |
|
d3 |
Переход от сохранения энергии к удару |
|
d4 |
Переход от удара к возврату |
|
d5 |
Переход от возврата к взводу |
|
d6 |
Переход к завершению работы системы на стадии взвода |
|
d7 |
Переход к завершению работы системы на стадии разгона |
Таблица 3
Список предусловий и постусловий
|
Предусловие |
Событие |
Постусловие |
|
b1 |
d1 |
b2 |
|
b2 |
d2 |
b5 |
|
b5 |
d3 |
b3 |
|
b3 |
d4 |
b4 |
|
b4 |
d5 |
b1 |
|
b1 |
d6 |
b1 |
|
b2 |
d7 |
b2 |
Формализация разработки алгоритмов управления мехатронными системами
Для решения этих задач необходимо исследовать сетевую модель по графу достижимости сети Петри. Согласно списку предусловий и постусловий строятся матрицы прямой и обратной функции инцидентности, которые выявляют входные и выходные события dj при выполнении или невыполнении условий bi.
По матрицам прямой и обратной функции инцидентности составляются уравнения (1), определяющие наличие метки в позиции bi после срабатывания перехода dj.
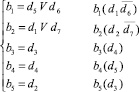 (1)
(1)
На основании уравнений составляется граф достижимости, который соответствует маршруту обхождения всех ребер сети Петри и матрица смежности графа достижимости Q с условиями pj срабатывания переходов di, которые напрямую зависят от информации от датчиков системы (табл. 4).
Таблица 4
Матрица Q
|
Разметка |
b1 |
b2 |
b5 |
b3 |
b4 |
|
b1 |
d6p6 |
d1p1 |
|||
|
b2 |
d7p7 |
d2p2 |
|||
|
b5 |
d3p3 |
||||
|
b3 |
d4p4 |
||||
|
b4 |
d5p5 |
Согласно информации от датчиков D1–D4 ‒ определяются все возможные условия срабатывания переходов и функций выходов, на базе которых строится граф Γ2. Граф Γ2 отображает разметку сети Петри, то есть выявляет все возможные состояния управляющей подсистемы и переходы между ними.
После построения графа Γ2 необходимо составить матрицу смежности Q, возведенную в квадрат, для определения цепей длины 2, которая выделяет из графа Γ2 все возможные нулевые и последующие переходы и состояния по ходу их следования от нулевого состояния. Минимизированная матрица  выявляет все необходимые состояния и переходы для работы подсистемы управления и контроля УМС. Выявленные состояния соответствуют выполняемым микрокомандам Ai подсистемы управления и контроля, которые включают в себя необходимые наборы микроопераций Aj для выполнения микрокоманд. Выявленные переходы αk, согласно условиям срабатывания, переводят подсистему управления и контроля УМС от выполнения одной команды к другой.
выявляет все необходимые состояния и переходы для работы подсистемы управления и контроля УМС. Выявленные состояния соответствуют выполняемым микрокомандам Ai подсистемы управления и контроля, которые включают в себя необходимые наборы микроопераций Aj для выполнения микрокоманд. Выявленные переходы αk, согласно условиям срабатывания, переводят подсистему управления и контроля УМС от выполнения одной команды к другой.
Для составления алгоритмов управления необходимо задать набор микрокоманд и микроопераций. Для каждой конкретной УМС определяется свой набор.
На основании управляемых параметров УМС [2] составляется таблица микроопераций и микрокоманд для системы управления и контроля УМС (табл. 5).
Таблица 5
Таблица микроопераций и микрокоманд
|
C0 |
Установка нулевого состояния |
|
|
C1 |
Запись кода |
|
|
C2 |
Считывание прямого кода D1 |
|
|
C3 |
Считывание обратного кода D1 |
|
|
C4 |
Считывание прямого кода D2 |
|
|
C5 |
Считывание обратного кода D2 |
|
|
C6 |
Считывание прямого кода D3 |
|
|
C7 |
Считывание обратного кода D3 |
|
|
C8 |
Считывание прямого кода D4 |
|
|
C9 |
Считывание обратного кода D4 |
|
|
C10 |
Переход в режим взвода |
|
|
C11 |
Переход в режим разгона |
|
|
C12 |
Переход в режим накопления энергии |
|
|
C13 |
Переход в режим удара |
|
|
C14 |
Переход в режим возврата |
|
|
Cош |
Сигнал ошибки переходов, остановка работы системы |
|
|
Cнаг |
Сигнал остановки устройства после завершения работы |
|
|
α0 |
Безусловный переход |
|
|
α1 |
D1 сработал |
|
|
α2 |
D3 сработал |
|
|
α3 |
D2 сработал |
|
|
α4 |
D4 сработал |
|
|
A1 |
Установка исходного состояния системы |
C0, C1, C2, C3, C6, C7 |
|
A2 |
Взвод системы |
C10, C4, C5, C8, C9 |
|
A3 |
Разгон системы |
C11 |
|
A4 |
Накопление энергии |
C12 |
|
A5 |
Удар |
C13 |
|
A6 |
Возврат системы в исходное состояние |
C14 |
|
A7 |
Подготовка к завершению работы системы |
Cош, Cнаг |
На основании табл. 5 для представленного примера получим алгоритм работы подсистемы управления и контроля УМС в форме логической схемы (ЛСА):
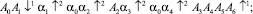
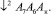
Полученный алгоритм является основой для построения микропрограммного автомата управления по методике работ [7–11]. Достоинством предложенной методики анализа и синтеза УМС является комплексный подход к проектированию как энергетических подсистем, реализуемых механическими средствами, так и информационно-управляющих подсистем УМС. При этом нет необходимости разделять проектирование обеих подсистем и решать в последующем как и какими средствами реализовать электронные средства контроля и управления УМС. Созданный по предлагаемой методике вариант реализации УМС сразу эмерджентно обладает свойствами безошибочного управления энергетическим каналом, так как учитывает сложную логическую структуру взаимосвязи состояний системы с последовательностью выдаваемых команд и средств контроля.
Заключение
В статье показана целесообразность представления мехатронных систем структурной моделью в виде функциональной, информационной, логической, адресной и управляющей подсистем.
Предложенный в статье метод системного анализа механических систем ударного действия на основе графовых структурных моделей и их анализ с применением математического аппарата сетей Петри позволяет определить правильность функционирования всех подсистем энергетического канала механических систем и одновременно формализовать процедуры управления. По полученным алгоритмам может быть построен автомат управления системой.
Рецензенты:
Марюхненко В.С., д.т.н., доцент кафедры «Автоматика и телемеханика», Иркутский государственный университет путей сообщения, г. Иркутск;
Лукьянов А.В., д.т.н., профессор, Иркутский государственный университет путей сообщения, г. Иркутск.
Работа поступила в редакцию 19.07.2013.
Библиографическая ссылка
Мухопад Ю.Ф., Мухопад А.Ю., Филатов Д.А., Мельников А.В. АНАЛИЗ МЕХАТРОННЫХ СИСТЕМ УДАРНОГО ДЕЙСТВИЯ // Фундаментальные исследования. 2013. № 8-6. С. 1337-1343;URL: https://fundamental-research.ru/ru/article/view?id=32133 (дата обращения: 20.02.2026).



