Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Суханова Е.И. 1 Ширнаева С.Ю. 1

---

1 ФГБОУ ВПО «Самарский государственный экономический университет»

В статье предложена методика отбора экзогенных и эндогенных переменных в систему одновременных уравнений с использованием коинтеграционного анализа временных рядов показателей, отражающих стабилизационные процессы экономики России. Предварительно временные ряды показателей были проверены на устойчивость и на причинно-следственную зависимость. Проверялась гипотеза о наличии коинтеграции временных рядов методом Энгла‒Грэнжера, в соответствии с которым определен порядок интегрируемости временных рядов экономических показателей I(1) (на основе выводов, полученных по автокорреляционной, частной автокорреляционной функциям и расширенному тесту Дики‒Фуллера); протестированы остатки парной регрессии между соответствующими переменными с использованием расширенного теста Дики‒Фуллера. Было получено, что рассмотренные пары временных рядов экономических показателей коинтегрированы. По исходным данным построена эконометрическая модель взаимосвязей экономических показателей, отражающих стабилизационные процессы экономики России, в виде системы одновременных уравнений. Полученная модель может быть использована для построения точечных и интервальных прогнозов рассмотренных экономических показателей.

Статья в формате PDF

586 KB

временные ряды

стационарность

коинтеграция

система одновременных уравнений

стабилизационные процессы

1. Краткосрочные экономические показатели Российской Федерации. – М., 2013. – URL: http://www.gks.ru/bgd/regl/b13_03/Main.htm (дата обращения: 19.03.2013).

2. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. – М.: Дело, 2004. – 575 с.

3. Суханова Е.И., Ширнаева С.Ю. Построение интервальных прогнозов эндогенных переменных одной эконометрической модели // Вестник Самарского государственного экономического университета. – Самара, 2013. – № 2(100). – С. 109–114.

4. Суханова Е.И., Ширнаева С.Ю. Статистические методы исследования макроэкономической стабилизации в России // Научные исследования Самарского государственного экономического университета: итоги и перспективы: сб. науч. тр.: в 2 ч. – Самара: Изд-во Самар. гос. экон. ун-та, 2011. – Ч.1. – С. 83–90.

5. Суханова Е.И., Ширнаева С.Ю. Типологизация показателей, отражающих стабилизационные процессы экономики России, по критериям устойчивости // Вестник Самарского государственного экономического университета. – Самара, 2012. – № 5(91). – С. 103–109.

6. Эконометрика: учебник / под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2002. – 344 с.

7. Engle R.F., Granger C.W.J. Cointegration and error correction: representation, estimation and testing // Econometrica. 1987. Vol. 55, pp. 251–276.

8. MacKinnon J.G. Critical values for cointegration tests // UC San Diego Discussion Paper, 1990, pp. 90–94.

При построении эконометрической модели в виде системы одновременных уравнений базовой задачей является отбор экзогенных и эндогенных переменных в модель. Обоснованный подход к решению данной задачи позволяет получить адекватную и качественную эконометрическую модель и дает возможность использовать ее для анализа и прогнозирования. Деление переменных на эндогенные и экзогенные определяется, прежде всего, содержательной стороной модели [2]. Требования, предъявляемые к набору переменных, вытекают из целей моделирования и сущности изучаемого экономического явления или процесса.

При моделировании такого макроэкономического явления, как стабилизационные процессы экономики России, выбор системы одновременных уравнений (СОУ) в качестве модели позволит провести всесторонний анализ взаимосвязей показателей, отражающих данные процессы. Если при этом переменные (показатели) представлены в виде временных рядов, то исследование этих рядов на наличие долговременной зависимости и определение направления этой зависимости становится неотъемлемой частью эконометрического моделирования стабилизационных процессов.

В ходе исследования был сформирован информационный массив, включающий ежемесячные статистические данные по 35 экономическим показателям России. Объем выборки составил 169 наблюдений за период с января 1999 года по январь 2013 года [1]. Обработка статистических данных проводилась с использованием пакетов прикладных программ Microsoft Excel и Econometric Views.

Сначала было проведено исследование устойчивости временных рядов всех рассмотренных показателей. В качестве критериев устойчивости использовались индекс устойчивости уровней, коэффициент устойчивости и ранговый коэффициент корреляции Спирмена [5].

При отборе эндогенных переменных (проверка устойчивости показала, что временные ряды всех отобранных эндогенных переменных устойчивы как по степени устойчивости уровней, так и по наличию необходимой тенденции изменения) использовалось определение стабилизации [4]. Под стабилизацией экономики понимается процесс приведения экономической системы в стабильное состояние, для которого характерен ряд признаков. Основные признаки стабилизации экономики и экономические показатели, поведение которых отражает соответствующие признаки, представлены в табл. 1.

Таблица 1

Экономические показатели (эндогенные переменные), отражающие стабилизационные процессы экономики России

К временным рядам всех показателей (сезонная составляющая была удалена) был применен тест Грэнжера на причинно-следственную зависимость [2], позволивший определить направление причинно-следственных связей рассмотренных экономических показателей. Следует отметить, что данный тест является чувствительным к количеству лагов, поэтому он проводился для величины лага от 2 до 6 месяцев. Учитывая результаты исследования устойчивости временных рядов, а также результаты применения теста Грэнжера, в качестве экзогенных переменных были отобраны следующие показатели: коммерческий грузооборот транспорта, млрд т-км (X1); погрузка грузов на железнодорожном транспорте, млн т (X2); объем работ по виду деятельности «Строительство», млрд руб. (X3); официальный курс доллара, руб. за 1 долл. США (X4); оборот розничной торговли, млрд руб. (X5); объем платных услуг населению, млрд руб. (X6); денежные доходы в среднем на душу населения, руб. (X7); просроченная кредиторская задолженность организаций в бюджет, млрд руб. (X8); просроченная дебиторская задолженность организаций, млрд руб. (X9); средние цены производителей на нефть, руб. за 1 т (X10); средние цены производителей на газ горючий, руб. за 1 тыс. м3 (X11).

Характерной особенностью временных рядов большинства показателей, отражающих стабилизационные процессы экономики России, является их нестационарность. Наличие в данных рядах тренда наряду с наличием сезонной составляющей, при применении к ним традиционных методов корреляционного и регрессионного анализа может привести к явлениям ложной корреляции и мнимой регрессии [2]. С целью применения этих методов временные ряды рассмотренных показателей были проверены на коинтеграцию.

Под коинтеграцией будем понимать зависимость в уровнях двух (или более) временных рядов, которая выражается в совпадении или противоположной направленности их тенденций и случайной колеблемости [6]. Нестационарные временные ряды Xtи Yt называются коинтегрированными, если существует линейная комбинация этих рядов, представляющая собой стационарный временной ряд.

Для проверки наличия коинтеграции двух временных рядов Xtи Yt в данной работе использовался метод Энгла–Грэнжера [7], в соответствии с которым исследование проводилось по следующей схеме:

1) определялся порядок интегрированности данных временных рядов;

2) с помощью метода наименьших квадратов оценивалось уравнение регрессии Yt = a + bXt + εt (называемое уравнением коинтеграции);

3) с помощью теста Дики–Фуллера остатки регрессии et данного уравнения исследовались на стационарность; основная гипотеза состояла в том, что Xtи Yt не коинтегрированы;

4) если по результатам теста Дики–Фуллера остатки et оказывались стационарными, то основная гипотеза отвергалась, а временные ряды Xtи Yt являлись коинтегрированными.

При применении метода Энгла–Грэнжера использовались специально разработанные таблицы критических точек [8].

Коинтегрированными могут быть только такие два временных ряда, которые имеют одинаковый порядок интегрированности. Зная порядок интегрированности временных рядов рассматриваемых экономических показателей, можно подобрать преобразование временного ряда, которое обеспечит его стационарность. Это, в свою очередь, делает применение эконометрических методов корректным и позволяет избежать мнимой регрессии.

Определение порядка интегрированности временных рядов переменных рассмотрим на примере экзогенной переменной X1 – коммерческий грузооборот транспорта (млрд т-км). Динамика изменения временного ряда данной переменной (сезонная составляющая удалена) представлена на рис. 1.

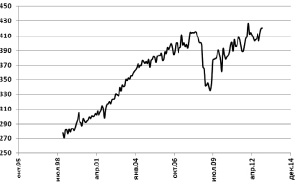
Рис. 1. Динамика коммерческого грузооборота транспорта (X1) за период с января 1999 года по январь 2013 года

Анализ динамики позволяет предположить, что исходный временной ряд не является стационарным (имеет место возрастающий линейный тренд). Для подтверждения этого предположения были построены автокорреляционная (АКФ) и частная автокорреляционная (ЧАКФ) функции данного временного ряда (рис. 2).

Рис. 2. Автокорреляционная и частная автокорреляционная функции временного ряда переменной X1 (фрагмент)

Анализ рис. 2 показал, что АКФ показателя X1 (коммерческий грузооборот транспорта) экспоненциально убывает, а ЧАКФ имеет наибольшее сильно выделяющееся значение коэффициента автокорреляции первого порядка и не имеет значимых коэффициентов автокорреляции других порядков. Это означает, что временной ряд данного показателя представляет собой модель авторегрессии первого порядка AR(1), то есть не является стационарным.

Еще одним способом проверки временного ряда на стационарность является расширенный тест Дики–Фуллера (ADF-тест) (используется распределение t-статистики, описанное Дики и Фуллером), который был применен для проверки основной гипотезы о нестационарности временного ряда. Вычисленное наблюдаемое значение t-статистики ADF-теста, а также критические значения представлены в табл. 2.

Из табл. 2 видно, что основная гипотеза не отвергается на рассмотренных уровнях значимости (1, 5 и 10 %). Таким образом, как графики АКФ и ЧАКФ, так и результаты ADF-теста показывают, что временной ряд переменной X1 не является стационарным. Для получения стационарного временного ряда к нему была применена операция взятия первых разностей. График преобразованного временного ряда переменной X1, графики АКФ и ЧАКФ, а также результаты ADF-теста представлены на рис. 3, 4 и в табл. 3.

Таблица 2

Результаты расширенного теста Дики–Фуллера для переменной X1

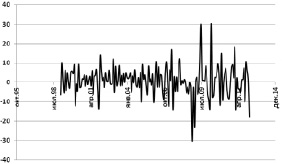
Рис. 3. Временной ряд первых разностей для переменной (коммерческий грузооборот транспорта) за период с января 1999 года по январь 2013 года

Рис. 4. Автокорреляционная и частная автокорреляционная функции первых разностей временного ряда переменной X1 (фрагмент)

Так как ни один из коэффициентов автокорреляции у АКФ и ЧАКФ не является значимым, то можно предположить, что временной ряд первых разностей переменной X1 является стационарным. Для проверки данного предположения был проведен расширенный ADF-тест по первым разностям уровней этой переменной (табл. 3)

Таблица 3

Результаты расширенного теста Дики–Фуллера для первых разностей временного ряда переменной X1

Таким образом, по результатам ADF-теста гипотеза о нестационарности временного ряда (наличии единичного корня) отвергается на всех рассмотренных уровнях значимости, следовательно, ряд первых разностей переменной X1 является стационарным, а исходный ряд – интегрированным первого порядка I(1).

Анализируя результаты исследования свойств временных рядов остальных экзогенных и эндогенных переменных, было получено, что они являются нестационарными с порядком интегрированности I(1). В свою очередь, первые разности данных временных рядов являются стационарными, то есть имеют порядок интегрированности I(0).

Результаты проведенного анализа показали, что временные ряды рассматриваемых показателей могут быть подвергнуты коинтеграционному анализу для выявления долговременных связей между ними. Далее в работе проводился коинтеграционный анализ пар временных рядов экономических показателей, у которых ранее (с помощью теста Грэнжера) было выявлено наличие причинно-следственной зависимости.

Исследуем временные ряды показателей X7 (денежные доходы в среднем на душу населения) и Y5 (начисленная среднемесячная номинальная заработная плата одного работника) на коинтеграцию. С этой целью было построено графическое изображение динамики изменения временных рядов данных показателей (рис. 5).

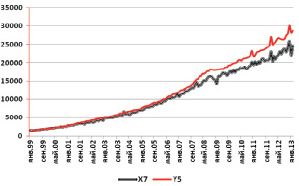
Рис. 5. Динамика денежных доходов в среднем на душу населения (X7) и начисленной среднемесячной номинальной заработной платы одного работника (Y5) за период с января 1999 года по январь 2013 года

Графический анализ динамики временных рядов показателей Y5 и X7 показал, что их тенденции совпадают. Чтобы исключить возможность ложной корреляции (согласно методу Энгла–Грэнжера), остатки модели парной линейной зависимости Y5 и X7 были исследованы на стационарность. С помощью метода наименьших квадратов (МНК) было получено следующее выборочное уравнение парной линейной зависимости:

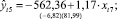R2 = 0,995.

Далее выдвигалась основная гипотеза: временные ряды показателей Y5 и X7 не коинтегрированы. Для проверки основной гипотезы были найдены остатки регрессии et полученного уравнения, которые исследовались на стационарность с помощью расширенного теста Дики–Фуллера (табл. 4).

По результатам ADF–теста остатки регрессии et стационарны, следовательно, нулевая гипотеза об отсутствии коинтеграции между временными рядами показателей Y5 и X7 отвергается. Таким образом, временные ряды исследуемых показателей Y5 и X7 коинтегрированы.

Аналогично исследовались пары временных рядов каждой переменной правой части уравнений СОУ с каждой зависимой переменной 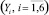левой части уравнений СОУ. Были вычислены наблюдаемые значения t-статистики расширенного теста Дики–Фуллера для каждой пары переменных. Результаты расчетов представлены в табл. 5.

Таблица 4

Результаты расширенного теста Дики–Фуллера для остатков регрессии et

Таблица 5

Наблюдаемые значения t-статистики ADF-теста

На основе полученных результатов был сделан вывод о том, что рассмотренные пары временных рядов отобранных экономических показателей коинтегрированы на 10 %-м уровне значимости (критическое значение теста Дики-Фуллера при 10 %-м уровне значимости равно –1,62). Полученные выводы были использованы при построении эконометрической модели стабилизационных процессов в виде СОУ, в которой в качестве исходных данных использовались непосредственно уровни рассматриваемых рядов. Это позволило учесть информацию, содержащуюся в исходных данных, в полном объеме, не переходя, например, к первым разностям уровней. Полученный результат особенно важен при исследовании стабилизационных процессов, так как в этом случае нужно учитывать наличие необходимой для общества тенденции развития. Моделирование таких процессов без учета тенденции не позволит проанализировать долговременную зависимость между переменными и получить качественный прогноз.

Учитывая результаты коинтеграционного анализа, была получена структурная форма СОУ следующего вида:

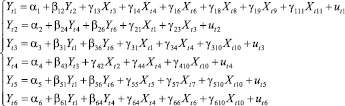
где uti – случайные компоненты; αi, αik, γip – структурные параметры, которые были оценены по выборке ( ).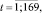

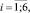
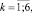
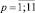После оценивания структурных параметров предложенной модели двухшаговым методом наименьших квадратов (так как проверка условий идентифицируемости показала, что все уравнения СОУ сверхидентифицируемы) была получена следующая система уравнений:

Построенная эконометрическая модель удовлетворяет требованиям адекватности. Практически все оценки параметров уравнений регрессии статистически значимы на 5 %-м уровне значимости (в модели в скобках указаны расчетные значения t-статистики для соответствующих оценок параметров, здесь же указаны значения коэффициентов детерминации R2). Статистически значимы (по F-критерию) и все уравнения системы.

Полученная система одновременных уравнений может быть использована для анализа структуры взаимосвязей рассмотренных экономических показателей, а также для построения точечных и интервальных прогнозов [3].

Рецензенты:

Корнеева Т.А., д.э.н., профессор кафедры бухгалтерского учета и экономического анализа, ФГБОУ ВПО «Самарский государственный экономический университет», г. Самара;

Репин О.А., д.ф.-м.н., профессор, заведующий кафедрой математической статистики и эконометрики, ФГБОУ ВПО «Самарский государственный экономический университет», г. Самара.

Библиографическая ссылка