Большинство роботов, перемещающихся с отрывом от поверхности, также называющихся прыгающими, в качестве модуля, разгоняющего устройство и позволяющего отрываться от поверхности, используют ногу, состоящую из нескольких звеньев, которые могут образовывать пары вращательного или поступательного движения [6–11]. Приземление прыгающих роботов может происходить как на ногу, так и на корпус, в первом случае нога должна изготавливаться с учетом ударных нагрузок при приземлении, а во втором этого не требуется, нога может быть достаточно легкой и менее прочной, корпус устройства при этом чаще всего оснащается упруго-вязкими элементами для гашения удара.
В работе представлен прыгающий робот, технология прыжка которого основывается на втором случае, т.е. разгон осуществляется при помощи ноги, а приземление происходит на корпус. Особенностью исследуемого робота является то, что нога может поворачиваться внутри корпуса на любой требуемый угол, когда последний взаимодействует с поверхностью, это означает, что независимо от стороны корпуса, на которую произойдет приземление, робот сможет совершить следующий прыжок под необходимым углом к горизонту.
Целью данной работы является выявление влияния параметров робота на условия приземления, т.е. на точки корпуса, которые будут находиться на поверхности после прыжка объекта и с которых будет проходить следующий прыжок.
Описание прыгающего робота
Исследуемый четырехзвенный прыгающий робот состоит из звеньев 1–4, звено 1 которого является стопой, звенья 2 и 3 представляют собой телескопическую ногу, а звено 4 – корпус (рис. 1, а). Приводы 5 и 6, установленные на звеньях 4 и 2 соответственно, обеспечивают повороты звеньев 3 и 1 относительно звеньев 4 и 2. Привод 7, закрепленный на звене 2, позволяет звеньям 2 и 3 поступательно перемещаться друг относительно друга. Привод 7 включает в себя двигатель 8, жестко связанный с ним кулачок 9, и пружины 10. Взвод пружин осуществляется кулачком, а их подвижные концы соединены со звеном 2 ноги. Робот периодически контактирует с горизонтальной опорной поверхностью [2, 4, 5].
а 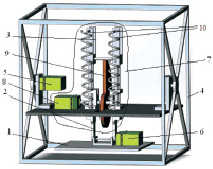 б
б 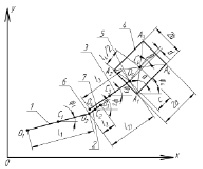
Рис. 1. Прыгающий робот: а – конструктивная схема; б – расчетная схема
Каждый прыжок объекта представляет собой последовательность этапов, характеризующихся определенными видами движения звеньев [3]. В начальный момент времени корпус робота находится на поверхности, звенья 1–3 втянуты в него и зафиксированы под произвольными углами. На первом этапе происходит поворот звеньев 1–3, жестко связанных между собой, приводом 5 относительно точки закрепления в корпусе до достижения некоторого заданного значения угла 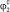 наклона звена 2 к поверхности. После чего на втором этапе звено 1 поворачивается приводом 6 на угол, при котором оно будет параллельно поверхности. На следующем (третьем) этапе наблюдается перемещение звеньев 1 и 2 приводом 7 до взаимодействия звена 1 с поверхностью, после чего (четвертый этап) происходит разгон звеньев 3 и 4 тем же приводом до отрыва звена 1 от поверхности, звенья робота при этом приобретают скорость
наклона звена 2 к поверхности. После чего на втором этапе звено 1 поворачивается приводом 6 на угол, при котором оно будет параллельно поверхности. На следующем (третьем) этапе наблюдается перемещение звеньев 1 и 2 приводом 7 до взаимодействия звена 1 с поверхностью, после чего (четвертый этап) происходит разгон звеньев 3 и 4 тем же приводом до отрыва звена 1 от поверхности, звенья робота при этом приобретают скорость 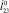 . Полет робота, характеризующийся отсутствием взаимодействия всех точек объекта с поверхностью, соответствует пятому этапу, при этом звенья 1 и 2 полностью втягиваются в корпус силой
. Полет робота, характеризующийся отсутствием взаимодействия всех точек объекта с поверхностью, соответствует пятому этапу, при этом звенья 1 и 2 полностью втягиваются в корпус силой 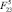 , генерируемой приводом 7. Этап приземления (шестой этап) наступает, когда одна или две точки корпуса начнут контактировать с поверхностью, после чего происходит позиционирование объекта (седьмой этап) до тех пор, пока две точки корпуса не будут взаимодействовать с поверхностью. После этого прыжок завершится. Значения моментов и силы, создаваемых приводами 5–7, будем считать постоянными на каждом из этапов прыжка, а временные интервалы этапов – переменными, что позволяет роботу реализовывать прыжки под разными углами к горизонту и с разной начальной скоростью.
, генерируемой приводом 7. Этап приземления (шестой этап) наступает, когда одна или две точки корпуса начнут контактировать с поверхностью, после чего происходит позиционирование объекта (седьмой этап) до тех пор, пока две точки корпуса не будут взаимодействовать с поверхностью. После этого прыжок завершится. Значения моментов и силы, создаваемых приводами 5–7, будем считать постоянными на каждом из этапов прыжка, а временные интервалы этапов – переменными, что позволяет роботу реализовывать прыжки под разными углами к горизонту и с разной начальной скоростью.
Математическая модель прыгающего робота
Расчетная схема исследуемого робота приведена на рис. 1, б. Введем абсолютную неподвижную систему координат Оху, в которой будем рассматривать прыжок устройства с горизонтальной шероховатой поверхности, совпадающей с осью Ох. Положим, что звенья 1–4 представляют собой абсолютно твердые тела, причем звенья 1–3 являются стержнями длинами li, звено 4 – прямоугольником А1А2А3А4 с размерами 2а×2b. Каждое звено робота обладает массой mi, которая сосредоточена в центре его симметрии – точке Сi. Длина ноги определяется расстоянием l23 между точками О2 и О5, положение последней в корпусе определяется расстоянием l4/2 и углом β между прямой, соединяющей точки С4 и О5, и стороной корпуса А1А4.
Вектор координат, описывающий положение звеньев робота, имеет вид
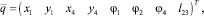 (1)
(1)
где х1, y1, х4, у4 – координаты центров масс звеньев 1 и 4, φ1, φ2 и φ4 – углы поворота звеньев 1, 2 и 4, l23 – длина ноги робота.
Система дифференциальных уравнений, описывающих движение робота, записывается с использованием уравнений Лагранжа второго рода. Кинетическая энергия системы и i-го звена определяются по формулам
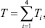 (2)
(2)
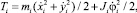 (3)
(3)
где 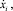
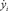 – проекции скорости центра масс i-го звена на оси Ох и Оу;
– проекции скорости центра масс i-го звена на оси Ох и Оу; 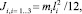
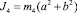 – центральные моменты инерции звеньев;
– центральные моменты инерции звеньев; 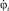 – угловая скорость i-го звена.
– угловая скорость i-го звена.
Дифференциальные уравнения движения робота представим в матричной форме
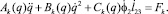 (4)
(4)
Матрицы Ak(q), Bk(q), Ck(q), Fk определяются на каждом из этапов k движения робота в соответствии с разработанной технологией движения.
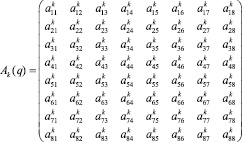 ; (5)
; (5)
– матрица коэффициентов при ускорениях,
 (6)
(6)
– матрица коэффициентов при центробежных силах инерции,
 (7)
(7)
– матрица коэффициентов при силах Кориолиса,
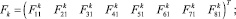 (8)
(8)
– матрица обобщенных сил.
В качестве модели взаимодействия звеньев 1 и 4 с поверхностью будем рассматривать силу симметричного сухого трения, которая будет возникать в одной из крайних точек каждого звена [1]. Причем ограничимся случаем, когда модуль силы трения не будет превышать предельного значения, это означает, что точка опоры с силой трения будет неподвижно зафиксирована на поверхности.
Моделирование движения робота
Для моделирования движения робота разработанная математическая модель реализации одного прыжка преобразована к безразмерному виду при помощи масштабных коэффициентов М = 0,05 кг, Т = 0,1 с, L = 0,1 м. Массогабаритные характеристики объекта: m1 = 1, m2 = 1, m3 = 1, m4 = 7, а = 1, b = 1, l1 = 0,5, l2 = 0,9, l3 = 0,9,  = 0,4,
= 0,4, 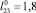 . Начальные условия моделирования: t = 0, x4 = а,
. Начальные условия моделирования: t = 0, x4 = а, 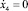 , y4 = b,
, y4 = b, 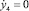 , j4 = 0,
, j4 = 0, 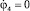 , j1 = π,
, j1 = π, 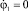 , j2 = π/2,
, j2 = π/2, 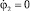 .
.
В работе определены зависимости точек корпуса, на которые будет происходить приземление робота, от ряда варьируемых параметров, в качестве которых рассматриваются: угол β и расстояние l4, определяющие положение точки закрепления ноги в корпусе, скорость 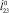 , достигаемая объектом к началу этапа полета, сила
, достигаемая объектом к началу этапа полета, сила 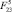 , посредством которой происходит втягивание звеньев 1 и 2 в корпус во время полета, и угол
, посредством которой происходит втягивание звеньев 1 и 2 в корпус во время полета, и угол 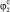 , под которым приложена сила, обеспечивающая отрыв робота от поверхности.
, под которым приложена сила, обеспечивающая отрыв робота от поверхности.
По приведенным на рис. 2, 3, 5 диаграммам точек приземления робота видно, что при прохождении силы, отрывающей робота от поверхности, через центр масс корпуса последнего (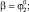 ,
, 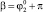 ) во время этапа полета корпус не вращается относительно точки С4 (φ4 = 0) и приземление осуществляется одновременно на две точки корпуса А1А4, с которых происходил отрыв от поверхности (область 0). При диапазонах угла
) во время этапа полета корпус не вращается относительно точки С4 (φ4 = 0) и приземление осуществляется одновременно на две точки корпуса А1А4, с которых происходил отрыв от поверхности (область 0). При диапазонах угла 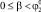 ,
, 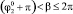 (область 1) на этапе полета робот поворачивается против часовой стрелки на угол, не превышающий π/2 (рис. 4, в), поэтому первой точкой приземления является А1, на седьмом этапе (этапе приземления) наблюдается вращение робота по часовой стрелке до тех пор, пока корпус не начнет взаимодействовать с поверхностью во второй точке – А4. При угле
(область 1) на этапе полета робот поворачивается против часовой стрелки на угол, не превышающий π/2 (рис. 4, в), поэтому первой точкой приземления является А1, на седьмом этапе (этапе приземления) наблюдается вращение робота по часовой стрелке до тех пор, пока корпус не начнет взаимодействовать с поверхностью во второй точке – А4. При угле 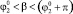 корпус робота во время полета вращается по часовой стрелке (рис. 4, в), угол поворота не достигает значения –π/2, поэтому первой точкой приземления будет А4. Вторая точка может изменяться, что видно по диаграммам, в области 2 это будет точка А1, когда поворот робота по часовой стрелке на этапе приземления не превышает π/4 (рис. 4, а), а в области 3 – А3, что возможно при невыполнении указанного условия (рис. 4, б). Граница между областями 2 и 3 представляет собой кривую, приближающую параболу, выпуклость которой направлена вниз, независимо от третьего варьируемого параметра –
корпус робота во время полета вращается по часовой стрелке (рис. 4, в), угол поворота не достигает значения –π/2, поэтому первой точкой приземления будет А4. Вторая точка может изменяться, что видно по диаграммам, в области 2 это будет точка А1, когда поворот робота по часовой стрелке на этапе приземления не превышает π/4 (рис. 4, а), а в области 3 – А3, что возможно при невыполнении указанного условия (рис. 4, б). Граница между областями 2 и 3 представляет собой кривую, приближающую параболу, выпуклость которой направлена вниз, независимо от третьего варьируемого параметра – 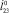 ,
, 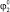 и l4.
и l4.
Причем чем дальше от центра масс корпуса расположена точка О5 закрепления ноги, т.е. чем больше расстояние l4, тем при меньшем значении силы 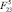 будет осуществляться переход из второй области в третью при
будет осуществляться переход из второй области в третью при 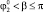 , и, наоборот, для
, и, наоборот, для 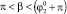 переход с ростом l4 будет наблюдаться при большем значении (рис. 2).
переход с ростом l4 будет наблюдаться при большем значении (рис. 2).
а 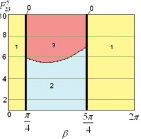 б
б 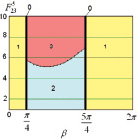 в
в 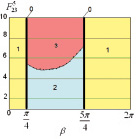
Рис. 2. Диаграммы точек приземления робота при 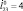 ,
, 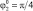 : а – l4 = 0,1; б – l4 = 0,15; в – l4 = 0,2; 0 – φ4 = 0, приземление на две точки А1А4 одновременно;1 – приземление на точки А1А4, 2 – приземление на точки А4А1, 3 – приземление на точки А4А3
: а – l4 = 0,1; б – l4 = 0,15; в – l4 = 0,2; 0 – φ4 = 0, приземление на две точки А1А4 одновременно;1 – приземление на точки А1А4, 2 – приземление на точки А4А1, 3 – приземление на точки А4А3
По диаграммам рис. 3 видно, что пороговое значение силы 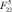 , при котором происходит переход из области 2 в область 3, возрастает с уменьшением скорости
, при котором происходит переход из области 2 в область 3, возрастает с уменьшением скорости 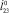 , достигаемой объектом к моменту отрыва от поверхности, т.к. чем меньше значение
, достигаемой объектом к моменту отрыва от поверхности, т.к. чем меньше значение 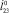 , тем меньше будет модуль угла поворота корпуса в полете (рис. 4, в).
, тем меньше будет модуль угла поворота корпуса в полете (рис. 4, в).
Анализируя диаграммы, показанные на рис. 5, можно сделать вывод о том, что граница между областями 2 и 3 будет проходить при меньшей силе 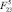 с увеличением угла
с увеличением угла 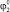 .
.
а 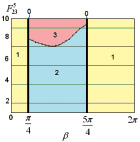 б
б 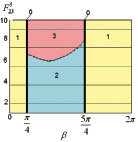 в
в 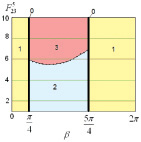
Рис. 3. Диаграммы точек приземления робота при l4 = 0,1, 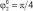 : а –
: а – 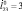 ; б –
; б – 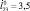 ; в –
; в – 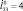 ; 0 – φ4 = 0, приземление на две точки А1А4 одновременно:1 – приземление на точки А1А4; 2 – приземление на точки А4А1; 3 – приземление на точки А4А3
; 0 – φ4 = 0, приземление на две точки А1А4 одновременно:1 – приземление на точки А1А4; 2 – приземление на точки А4А1; 3 – приземление на точки А4А3
а 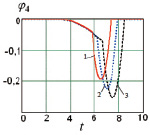 б
б 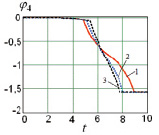 в
в 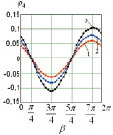
Рис. 4. Графики:а – φ4(t) при 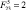 , β = π/2, б – φ4(t) при
, β = π/2, б – φ4(t) при 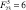 , β = π/2, в – φ4(β) при
, β = π/2, в – φ4(β) при 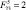 : 1 –
: 1 – 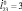 ; 2 –
; 2 – 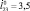 ; 3 –
; 3 – 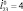 ; а –
; а – 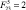 , б –
, б – 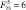
а 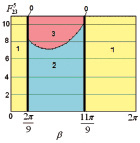 б
б 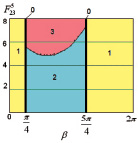 в
в 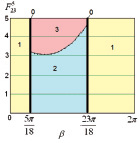
Рис. 5. Диаграммы точек приземления робота при l4 = 0,1, 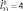 :а –
:а – 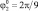 , б –
, б – 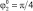 , в –
, в – 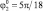 ; 0 – φ4 = 0, приземление на две точки А1А4 одновременно, 1 – приземление на точки А1А4, 2 – приземление на точки А4А1, 3 – приземление на точки А4А3
; 0 – φ4 = 0, приземление на две точки А1А4 одновременно, 1 – приземление на точки А1А4, 2 – приземление на точки А4А1, 3 – приземление на точки А4А3
Заключение
В статье рассмотрен четырехзвенный прыгающий робот, в качестве разгонного модуля использующий ногу, звенья которой могут позиционироваться относительно корпуса, когда последний находится на поверхности, приземление объекта происходит на корпус. Такая конструктивная схема позволяет объекту совершать прыжок с любой из сторон корпуса, что расширяет его функциональные возможности.
В работе в соответствии с разработанной математической моделью прыжка проведено численное моделирование движения робота и выявлено влияние ряда параметров объекта на условия приземления. Установлено, что в случае прохождения линия действия силы, обеспечивающей втягивание ноги в полете, через центр масс корпуса, вращения последнего в полете не происходит и приземление осуществляется на те же точки корпуса, которыми объект взаимодействовал в начале прыжка. В противном случае наблюдается поворот корпуса робота по или против часовой стрелки, причем при вращении против часовой стрелки точки приземления не меняются при вариации угла 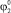 наклона разгоняющей силы, скорости
наклона разгоняющей силы, скорости 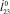 отрыва робота от поверхности, положения точки закрепления ноги (l4, β) и силы
отрыва робота от поверхности, положения точки закрепления ноги (l4, β) и силы 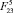 , с которой нога втягивается в полете, а при вращении по часовой стрелке при малых значениях параметров
, с которой нога втягивается в полете, а при вращении по часовой стрелке при малых значениях параметров 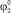 , l4,
, l4, 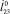 ,
, 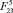 точки приземления остаются неизменными, а с увеличением указанных величин наблюдается увеличение угла поворота корпуса в полете и изменение точек приземления.
точки приземления остаются неизменными, а с увеличением указанных величин наблюдается увеличение угла поворота корпуса в полете и изменение точек приземления.
Рецензенты:
Кобелев Н.С., д.т.н., профессор, заведующий кафедрой теплогазоснабжения и вентиляции, ЮЗГУ, г. Курск;
Игнатенко Н.М., д.т.н., профессор, заведующий кафедрой общей и прикладной физики, ЮЗГУ, г. Курск.
Работа поступила в редакцию 15.07.2013.
Библиографическая ссылка
Пановко Г.Я., Яцун С.Ф., Локтионова О.Г., Волкова Л.Ю., Серебровский В.В. ДИНАМИКА ПРИЗЕМЛЕНИЯ ЧЕТЫРЕХЗВЕННОГОПРЫГАЮЩЕГО РОБОТА // Фундаментальные исследования. 2013. № 8-5. С. 1055-1060;URL: https://fundamental-research.ru/ru/article/view?id=32083 (дата обращения: 24.12.2025).



