Для изучения процесса развития остеоартоза выполняются различные типы экспериментальных исследований. Наиболее экономически выгодным и раскрывающим сущность фундаментального исследования является математическое моделирование [1‒9].
Для изучения патологического процесса нами совместно с кафедрой теории упругости и пластичности Нижегородского государственного университета им. Н.И. Лобачевского создана математическая модель питания суставного хряща.
Целью исследования является изучение процесса питания суставного хряща.
Материал и методы исследования
Для изучения развития изменений в питании суставных тканей была построена математическая модель. Гипотезой послужило предположение о мере интенсивности нагрузки, вызывающей патологические изменения в суставе, распределения питательных сред в хрящевой ткани, в частности распределения уровней внутрисуставной жидкости и артериальной крови субхондральной кости.
При исследовании процессов снабжения ткани хряща головки бедренной кости питательными веществами и кислородом с использованием математического моделирования ввели следующие основные предположения. Считаем, что во время всего процесса моделирования параметры системы неизменны: деградация свойств материалов вследствие отмирания тканей не учитывается, так как целью является изучение условий, приводящих к возможному отмиранию тканей. Характерным периодом времени, в течение которого нужно рассматривать процессы, происходящие в хряще, является период цикла нагружения TF. Обеспечение хрящевой ткани кислородом обусловлено уровнем артериальной крови в субхондральной кости C. Обеспечение хрящевой ткани питательными веществами обусловлено составом внутрисуставной жидкости U. Для упрощения задачи на первом этапе будем проводить моделирование в одномерной постановке, причем рассматривать задачу будем в декартовой системе координат, таким образом, проводится рассмотрение радиального столбца бесконечно малой площади поперечного сечения, вырезанного из хрящевой ткани и находящегося в наихудшей области.
При моделировании будем рассматривать радиальный столбик хрящевой ткани. Начало координат свяжем с головкой бедренной кости, тогда ордината x ∈ [0, l], где l – толщина хряща.
Для изучения распределения артериальной крови в субхондральной кости была создана следующая математическая модель.
С учетом соотношений и введенной выше системы координат начально-краевая задача для нахождения концентрацией артериальной крови в субхондральной кости C примет вид:
уравнение диффузии
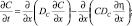
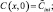
краевого условия на границе с бедренной костью
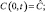
краевого условия на границе с тазом
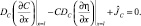
В соотношениях коэффициент диффузии определяется уравнением
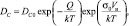
где DC0 – значение коэффициента диффузии для артериальной крови в субхондральной кости в случае нулевой температуры и нулевых напряжений.
Гидростатическое давление определяется по формуле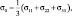 
при этом оно есть функция времени и пространства.
Для изучения распределения концентрации внутрисуставной жидкости в хряще предложена следующая математическая модель.
С учетом соотношений и введенной выше системы координат начально-краевая задача для нахождения концентрацией внутрисуставной жидкости в хряще U примет вид:
уравнение диффузии
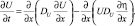
Для данного соотношения вводится коэффициент диффузии, который определяется выражением
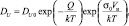
где DU0 – значение коэффициента диффузии для внутрисуставной жидкости в хряще в случае нулевой температуры и нулевых напряжений.
Для получения зависимости гидростатического давления от пространственных координат была построена 3D конечно-элементная модель, описывающая взаимодействие хряща головки бедренной кости и вертлужной впадины. Вид данной модели показан на рис. 1.
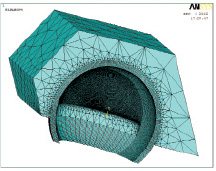
Рис. 1. Конечно-элементная модель взаимодействия хряща головки бедренной кости и вертлужной впадины
С использованием результатов конечно-элементного моделирования по направлению опасного радиуса в хряще была построена зависимость модуля гидростатического давления от координаты x. Указанная зависимость показана на рис. 2 как линия «данные». Для возможности дальнейшего использования полученных результатов указанные данные были аппроксимированы полиномом 4-й степени, имеющим вид
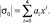
Исходя из особенностей геометрии тазобедренного сустава, характерный размер площадки контакта существенно больше толщины хряща. С учетом данного зависимость всех параметров напряженно-деформированного состояния в зоне контакта, в частности, и гидростатического давления, от усилия в суставе приближается к линейной.
Зависимость гидростатического давления от пространства и времени может быть описана следующей функцией
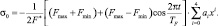
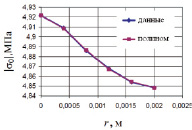
Рис. 2. Зависимость модуля гидростатического давления от пространственной координаты
В данном соотношении F* – то значение усилия в суставе, при котором были получены коэффициенты в полиноме. Знак «минус» появляется в связи с тем, что данное соотношение для величины, а не для модуля.
Результаты исследования и их обсуждение
Было проведено численное решение поставленных краевых задач. При этом предполагалось, что на начальный момент времени концентрация как артериальной крови в субхондральной кости, так и внутрисуставной жидкости в хряще равны нулю, то есть в соотношениях в правой части стоят нули. С учетом предположений, высказанных различными авторами, в качестве усилия в тазобедренном суставе было выбрано значение силы 4 кН. Данное значение было принято как максимальное значение силы, минимальное значение силы было принято равным нулю: Fmax = 4 кН и Fmin = 0 кН.
В качестве меры интенсивности нагружения хряща был рассмотрен период цикла нагружения. Данная величина была рассмотрена в диапазоне от 0,125 до 4 c. В качестве нормальных условий нагружения был рассмотрен период цикла нагружения, равный 2 c.
Распределения концентрации артериальной крови в субхондральной кости в конце цикла нагружения при различных значениях периода цикла нагружения, полученные по результатам решения начально-краевой задачи, приведены на рис. 3.
Распределения концентрации внутрисуставной жидкости в хряще в конце цикла нагружения при различных значениях периода цикла нагружения, полученные по результатам решения начально-краевой задачи, приведены на рис. 4.
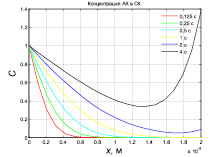
Рис. 3. Распределения концентрации артериальной крови в субхондральнойкости в конце цикла нагружения
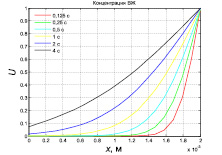
Рис. 4. Распределения концентрации внутрисуставной жидкости в хряще в конце цикла нагружения
Рассмотрена также суммарная концентрация питательных жидкостей в хряще, которая взята в виде алгебраической суммы концентраций C и U. Ее распределение в конце цикла нагружения при различных значениях периода цикла нагружения приведены на рис. 5.
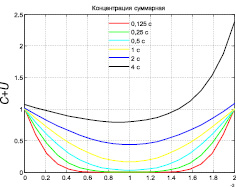
Рис. 5. Распределения концентрации питательных жидкостей в хряще в конце цикла нагружения
Для изучения влияния уровня максимальной нагрузки в цикле было проведено моделирование при нескольких значениях уровня нагрузки. Данная величина изменялась в диапазоне от 2 до 8 кН.
Анализ результатов численного моделирования позволяет сделать следующие выводы:
1) выбор в качестве меры интенсивности нагрузки при изучении картин распределения питательных сред в хрящевой ткани оказался верным: вид функции распределения концентрации внутрисуставной жидкости и артериальной крови субхондральной кости полностью определяется периодом цикла нагружения (данное утверждение также подтверждается результатами численного моделирования при различных значениям максимального усилия в цикле);
2) при периодах цикла нагружения, больших нормального (4 с), наблюдается повышенная концентрация артериальной крови на границе хрящевой и костной ткани;
3) при периодах цикла нагружения, меньших нормального (TF < 2 c), в толще хряща начинают появляться области, в которых уровни либо артериальной крови, либо внутрисуставной жидкости стремятся к нулю (является малой). Подобное явление должно приводить к недостаточности питания ткани хряща в данных областях и, как следствие, являться причиной последующей деградации ткани хряща.
Полученные результаты могут быть использованы для определения предельных допустимых интенсивностей нагрузок, не приводящих к деградации хрящевой ткани в изучаемом суставе на основании допускаемых уровней внутрисуставной жидкости [U] и артериальной крови субхондральной кости [C]. Смысл данных параметров следующий: если в какой-либо области хрящевой ткани уровень концентрации той или иной питательной среды к концу цикла нагружения ниже, чем введенные значения, то ткань может деградировать, а если больше либо равен данным параметрам, то ткань не деградирует за заданную базу эксперимента.
После введения допускаемых концентраций питательных жидкостей можно ввести по аналогии с механикой деформируемого твердого тела понятие предела выносливости хрящевой ткани. Под пределом выносливости хрящевой ткани будем понимать нагрузку с таким периодом нагружения TFR, что при нагрузке, характеризующейся любым периодом, большим данной величины, материал хряща не деградирует (в течение некоторой базы эксперимента), а при нагрузке с любым меньшим периодом нагружения материал хряща деградирует за конечный интервал времени.
Таким образом, математическое моделирование показало, что процесс диффузии питательных веществ зависит от характера нагрузки, что, в свою очередь, может приводить к развитию патологических изменений в суставном хряще.
Рецензенты:
Малышев Е.С., д.м.н., профессор кафедры хирургии факультета повышения квалификации врачей (курс травматологии и ортопедии), ГБОУ ВПО «НижГМА» Минздрава России, г. Н. Новгород;
Кудыкин М.В., д.м.н., профессор, ФГБУ «ННИИТО» Минздрава России, г. Н. Новгород;
Чалык Ю.В., д.м.н., профессор, кафедра общей хирургии Саратовского государственного медицинского университета, г. Саратов;
Пучиньян Д.М., д.м.н., профессор, зам.директора по науке, ФГБУ «Саратовский научно-исследовательский институт травматологии и ортопедии» Министерства здравоохранения и социального развития Российской Федерации, г. Саратов.
Работа поступила в редакцию 11.07.2013.
Библиографическая ссылка
Ежов М.Ю., Берендеев Н.Н., Петров С.В. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РАЗВИТИЯ ИЗМЕНЕНИЙ В СУСТАВНЫХ ТКАНЯХ ПРИ РАЗЛИЧНЫХ ПО ИНТЕНСИВНОСТИ ФИЗИЧЕСКИХ НАГРУЗКАХ // Фундаментальные исследования. 2013. № 7-3. С. 550-554;URL: https://fundamental-research.ru/ru/article/view?id=32053 (дата обращения: 02.04.2025).