Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Индыгашева Е.В. 1 Митянина О.Е. 1

---

1 ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет»

Управление, моделирование и анализ совмещенных процессов осложнены наличием нескольких стационарных состояний. Существующие методы анализа множественности стационарных состояний основаны на математических моделях процесса.В статье сформирована фундаментальная неравновесная модель реакционно-ректификационного процесса, предназначенная для оптимизации, анализа, проектирования совмещенных процессов. Был проведен расчет изменения количества вещества за счет массопереноса,рассчитаны коэффициенты массопереноса, удельная поверхность контакта фаз и движущая сила процесса реакционной ректификации. Было проведено сравнение полученной неравновесной модели с данными расчета [8] и равновесной моделью. Отклонение результата расчета по неравновесной модели от равновесной модели незначительно, поэтому для проектирования и моделирования совмещенных процессов рекомендовано использовать равновесную модель.

Статья в формате PDF

1464 KB

реакционная ректификация

неравновесная модель

метил-трет-бутиловый эфир (МТБЭ)

массоперенос

1. Астарита Дж. Масссопередача с химической реакцией. – М.: Химия, 1974. – 224 с.

2. Динамика нестационарной ректификации, совмещенной с реакцией переэтерификации в жидкой фазе / В.В. Дильман, В.А. Лотхов, А.А. Глаголева, Н.Н. Кулов, С.Я. Квашнин // Теоретические основы химической технологии. – 2002. – Т. 36, № 3. – С. 248.

3. Анализ равновесной и неравновесной моделей реакционно-ректификационной колонны синтеза МТБЭ / М.А. Самборская, О.Е. Митянина, А.В. Кравцов, К.В. Дерина // Нефтегазопереработка: тезисы докл. междунар. научно-практическая конф.(Уфа, 24–27 Мая 2011 г.). – Уфа, 2011 – С. 200–201.

4. Серафимов Л.А. Технология основного органического синтеза. Совмещённые процессы. – М.: Химия, 1993. – 410 с.

5. Ульянов Б.А., Бадеников В.Я., Ликучев В.Г. Процессы а аппараты химической технологии в примерах и задачах. – Ангарск, 2006. – С. 275–285.

6. Doherty M.F., Fidkowski Z.T., Malone M.F., Taylor R. Perry’s chemical engineers handbook, 8th edition, section 13, Distillation. – USA, The McGraw-Hill Companies, 2008. – Р. 50–51.

7. Hauan S., Hertxberg T. Why Methyl tert-Butyl Ether Production by Reactive Distillation May Yield Multiple Solutions – Industrial & Engineering Chemistry Research, 1995, no. 34(3).

8. Huss R.S., Chen F., Malone, Doherty M.F. Reactive distillation for methyl acetate production // Computers and Chemical Engineering. – 2003. – № 27. – Р. 1855–1866.

9. Murphree E.V. Reactive Column Calculations // Ind. Eng. Chem. – 1925. – № 17. – Р. 747–750.

10. Wang, S.J., Wang D.S.H., Lee E.K. Effect of Interaction Multiplicity on Control System Design for a MTBE Reactive Distillation Column // J. Proc. Contr. – 2003. – № 13. – Р. 503–515.

В последние годы в химической промышленности все большее значение приобретает такой технологический вариант процесса, как совместное проведение химический реакции с разделением реакционной смеси в одном и том же аппарате. Рациональное использование явления переноса массы в момент протекания химической реакции обеспечивает дополнительные преимущества как в кинетическом, так и в термодинамическом аспектах [1].

На сегодняшний день реакционно-ректификационные процессы приобретают все большую актуальность в силу того, что они имеют ряд технологических и экономических преимуществ перед стандартными схемами разделения. Таким образом, проектирование, исследование и внедрение данных процессов в производство является актуальной задачей для российской экономики. С целью создания более экономичной технологии, а также технологии безотходных производств очень часто выгодно проводить несколько процессов в одном аппарате.

В настоящее время опубликовано большое количество научных работ, посвященных моделированию и анализу динамического поведения процесса получения МТБЭ в колонне реакционной ректификации, в которых отмечается наличие множественных стационарных состояний с сильно различающимися выходами целевых продуктов, а также неидеальность парожидкостного равновесия [4, 7]. Поэтому качественное проектирование, исследование и оптимизация реакционной ректификации является актуальной научной и технологической задачей, для решения которой можно использовать популярное специализированное программное обеспечение на основе математических моделей.

Существует несколько основных типов моделей реакционной ректификации. Наиболее распространенной является равновесная модель, основным допущением которой является равновесие между жидкостью и паром. Подобные модели разрабатывались как за рубежом – в работах [8], так и в нашей стране [2]. Равновесные стационарная и динамическая модели, благодаря своей наглядности и простоте, успешно используются при проектировании, различных исследованиях и управлении реакционно-ректификационными аппаратами [10], авторы которых полагают, что для качественного исследования динамики реакционно-ректификационной колонны необходимо использовать модели, учитывающие неидеальность парожидкостного равновесия, то есть учитывающие массо- и теплоперенос в аппарате.

Задачами данной работы является формирование неравновесной математической модели реакционной ректификации, а также сравнение результатов расчета материального баланса колонны по равновесной и неравновесной модели.

На кафедре ХТТ и ХК ИПР ТПУ исследовалась равновесная модель реакционно-ректификационной колонны синтеза МТБЭ[3].

При расчете по неравновесной модели необходимо рассчитать изменение количества вещества на каждой из тарелок колонны за счет массопереноса [6].

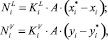(1)

где Ni – изменение количества вещества за счет массопереноса; Ki – коэффициент массопереноса, м/с; А – удельная поверхность контакта фаз, отнесенная к единице массы, м2/м2; xi, yi – средние составы жидкости и паров, поднимающиеся с i-й тарелки и поступающие на нее; 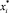,  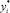– равновесный состав жидкости и пара i-ю тарелку.

Таким образом, для формирования неравновесной модели реакционной ректификации необходимо:

– определить коэффициенты диффузии;

– рассчитать коэффициент массопереноса;

– рассчитать площадь поверхности контакта фаз;

– рассчитать градиент концентрации.

Определение удельной поверхности контакта фаз на тарелках ректификационной колонны

Поверхность контакта фаз на тарелках ректификационной колонны трудно подается определению. Тем не менее разработаны методы и выполнены измерения поверхности. Ниже представлена формула, позволяющая рассчитать удельную поверхность, отнесенную к единице активной площади, для ситчатых тарелок [5].

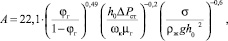(2)

где А – удельная поверхность контакта фаз, отнесенная к единице площади тарелки, м2/м2; φг – газосодержание, м3/м3; ΔРст – сопротивление столба жидкости, Н/м2; ΔPст = h0∙ρж∙g; h0 – высота слоя жидкости, м; wk – скорость газа в сечении колонны, м/с.

Высота запаса жидкости (h0) для ситчатых тарелок определяется по уравнению:

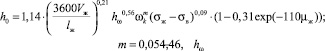(3)

где Vж – объемный расход жидкости, м3/с; lw – длина сливной перегородки, м; σж, σв – поверхностное натяжение жидкости и воды; hw – высота сливной перегородки, м; hf – высота пены, м; fc – доля свободного сечения тарелки [5].

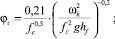(4)

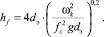(5)

В колоннах реакционной ректификации часто используется ситчатый тип тарелок.

Данные о характеристике ситчатых тарелок взяты из [5].

Таблица 1

Исходные данные

Пользуясь формулами (2)–(5), рассчитали удельную поверхность контакта фаз. Полученные результаты представлены в табл. 2.

Таблица 2

Расчетные данные удельной поверхности

После проведенных расчетов, получили удельную поверхность контакта фаз, отнесенной к единице площади тарелки, равной 9,204 м2/м2.

Расчет коэффициента массопереноса

Производительность массопереноса на тарелке часто выражается путем безразмерной группы, называемой числом единиц переноса [6].

Эти безразмерные числа определяются с помощью уравнений:

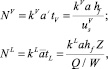(6)

где hf – высота пены, м; Z – длина пути потока жидкости, м; 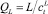 – объемная скорость потока жидкости, м3/с; us = V/ 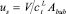– поверхностная скорость пара, м/с; Аbub – кипящий слой на тарелке, м2; hL – высота жидкости на тарелке, м; a’ – межфазная поверхность на единицу поверхности пара, м2/м3;  – межфазная поверхность на единицу поверхности жидкости, м2/м3.

Эти межфазные поверхности связаны с межфазной поверхности на единицу объема пены следующим образом:

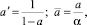(7)

где a = hL/hf – относительная плотность пены на тарелке. Также tL и tV время пребывания в паровой и жидкой фазах, определяются:

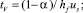(8)

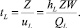(9)

Для определения числа единиц переноса мы используем корреляционную модель AIChE. В этой модели выражение для определения числа единиц переноса выглядит следующим образом:

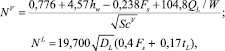(10)

где hw – высота перегородки, м; ScV – число Шмидта, равное ScV = μV/(ρVDV); Fs – фактор, кг/мс; Fs = usV(ρV)0,5; QL – объемная скорость потока жидкости, м3/с, 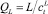[6].

Ниже представлена таблица с данными для расчета коэффициентов массопереноса.

Таблица 3

Данные для расчета коэффициента массопереноса

Данные для расчетов по тарелкам взяты из справочника программы Хайсис. Пользуясь формулами (6)–(11), рассчитали поэтапно коэффициенты массопереноса, средние значения коэффициентов массопереноса по тарелкам: kV = 0,491, kL = 147 м/с.

Определение движущей силы процесса

Движущую силу процесса рассчитываем, учитывая эффективность контактного устройства, используя закон Мерфри [9]:

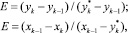(11)

где уk, уk-1 – средние составы паров, поднимающиеся с k-й тарелки и поступающие на нее; 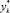– состав пара, равновесный с составом жидкости, покидающей k-ю тарелку; хk, хk-1 – средние составы жидкости, покидающие k-ю тарелку; 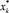* – состав жидкости, равновесный с составом пара, поднимающегося на k-ю тарелку.

После преобразований получили уравнение для расчета рабочей концентрации компонентов в паровой и жидкой фазах:

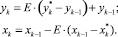(12)

Эффективность контактного устройства приняли среднее для ситчатых тарелок: Е = 0,8;

При расчете движущей силы процесса использовались равновесные концентрации на тарелках колонны синтеза МТБЭ, представленные в [7].

Расчет массопереноса

Сформированная неравновесная модель представлена ниже:

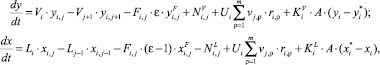(13)

где i – индекс компонента; j – индекс номера тарелки; x, y – мольная доля в жидкой и паровой фазах соответственно; V, L, F – расход пара, расход жидкости, расход орошающей жидкости соответственно, моль/с; U – удержание жидкости на тарелке, м/с;vi,ρ– стехиометрический коэффициент j-го вещества в реакции с номером ρ; ri,r – скорость химической реакции, моль/(м3·с).

Результаты расчета по неравновесной модели в сравнении с данными, представленными в [7] и с результатами расчета по равновесной модели для жидкой и паровой фазы, приведены на рис. 1 и 2 соответственно.

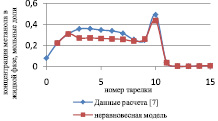
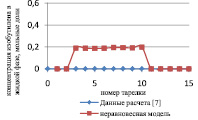
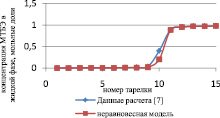
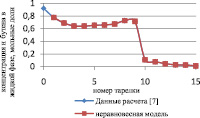
Рис. 1. Сравнение неравновесной модели с экспериментальными данными в жидкой фазе

Как видно из рис. 1, среднее отклонение расчетов в жидкой фазе по неравновесной модели от данных расчета [7] не превышает 3 %.

Как видно из рис. 2, отклонение расчета неравновесной модели от данных расчета [7] в паровой фазе превышает отклонение от данных расчета [7] в жидкой фазе, и можно сделать вывод, что неравновесная модель адекватно описывает процесс.

Сравнение результатов расчета неравновесной модели с результатами расчета по равновесной модели для жидкой и паровой фазы приведены на рис. 3 и 4 соответственно.

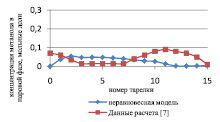
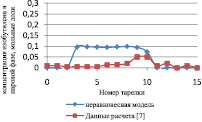
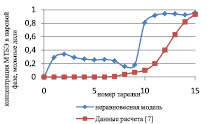
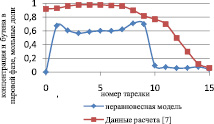
Рис. 2. Сравнение неравновесной модели с экспериментальными данными в паровой фазе

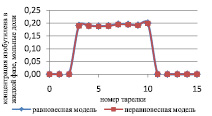
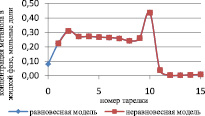
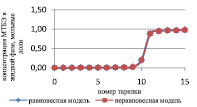
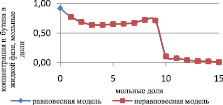
Рис. 3. Сравнение неравновесной и равновесной модели в жидкой фазе

Как видно из рис. 3 и 4, неравновесная модель практически не отличается от значений равновесной модели. Отклонения от значений равновесной модели составили не более чем 4 %, поэтому целесообразно использовать для расчетов, моделирования, проектирования, анализа множественности стационарных состояний и оптимизации равновесную модель.

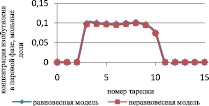
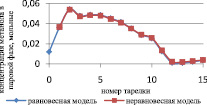
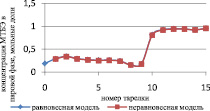
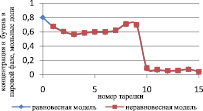
Рис. 4. Сравнение неравновесной и равновесной модели в паровой фазе

Рецензенты:

Ивашкина Е.Н., д.х.н., доцент кафедры химической технологии топлива и химической кибернетики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Томск;

Иванчина Э.Д., д.т.н., профессор кафедры ХТТиХК, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Томск.

Работа поступила в редакцию 01.07.2013.

Библиографическая ссылка