Трудовой потенциал страны, конкретного региона является на сегодняшний день одним из важных индикаторов экономического развития данных субъектов: в условиях демографического кризиса в нашей стране он позволяет указать потенциальные возможности устойчивого экономического роста субъекта [2, 3].
Исследования по вопросам формирования и использования трудового потенциала региона немногочисленны и имеют описательный характер. Они должны использовать различные методы: экономические, социальные, математические и т.д., которые позволяют оценить влияния трудового потенциала на экономическое развитие и обосновать способы управления им [1, 4].
В данной работе предложена экономико-математическая модель оптимального распределения трудового потенциала региона по отраслям экономики, которая апробирована на статистических данных по Ставропольскому краю.
Обозначим через A (человек) – общее число трудового потенциала региона, распределенного по различным отраслям экономики. Пусть в регионе выделено n-отраслей экономики (в том числе и такая специфическая отрасль, как «безработица»). Пронумеруем отрасли числами 1, 2, ..., n. Пусть в 1-й отрасли работает на данный момент времени k1 человек, во 2-й – k2 человек, ..., в n-й отрасли (для определенности считаем, что эта отрасль – «безработица») – kn человек. Тогда,
k1 + k2 + ... + kn = A.
Пусть за одну единицу времени, например, за один год, вложения (затраты) региона (в у.е. – условных единицах) в 1-ую отрасль региона составляют q1 (у. е.), во 2-ю – q2 (у. е.), ..., в n-ю отрасль – qn (у. е.). Общая сумма вложений составляет
q1 + q2 + ... + qn = Q (у. е.).
Обозначим через p1 (у. е.) – доход, полученный регионом за счет 1-й отрасли (за год), p2 (у. е.) – за счет 2-й отрасли, …, pn (у. е.) – за счет n-ой отрасли. Суммарный доход составляет
p1 + p2 + ... + pn = P (у. е.).
Можно рассчитать, какой доход принесет один работник своей отрасли за единицу времени, т.е. один год:
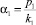 (у. е.) – средний доход, который приносит региону один работник 1-й отрасли;
(у. е.) – средний доход, который приносит региону один работник 1-й отрасли;
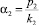 (у. е.) – средний доход, который приносит региону один работник 2-й отрасли;
(у. е.) – средний доход, который приносит региону один работник 2-й отрасли;
…….....................................……………
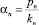 (у. е.) – средний доход, который приносит региону один работник n-й отрасли (так как на данный момент работник n-ой отрасли по соглашению является безработным, то он требует определенных вложений на свое содержание, т.е. приносит убыток региону; следовательно, αn будет отрицательным числом).
(у. е.) – средний доход, который приносит региону один работник n-й отрасли (так как на данный момент работник n-ой отрасли по соглашению является безработным, то он требует определенных вложений на свое содержание, т.е. приносит убыток региону; следовательно, αn будет отрицательным числом).
Рассмотрим затраты за единицу времени из бюджета региона на каждого работника по отраслям:
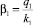 (у. е.) – среднее значение вложений из бюджета региона в работника 1-й отрасли;
(у. е.) – среднее значение вложений из бюджета региона в работника 1-й отрасли;
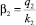 (у. е.) – среднее значение вложений из бюджета региона в работника 2-й отрасли;
(у. е.) – среднее значение вложений из бюджета региона в работника 2-й отрасли;
………….....................................………
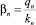 (у. е.) – среднее значение вложений из бюджета региона в работника n-й отрасли.
(у. е.) – среднее значение вложений из бюджета региона в работника n-й отрасли.
Будем предполагать, что полученные таким образом величины αi, βi, i = 1, ..., n, являются постоянными на некотором интервале времени [0; T]. На этом интервале времени изменяются следующие величины:
x1 – количество работников, занятых в 1-й отрасли;
x2 – количество работников, занятых во 2-й отрасли;
..................................................................
xn – количество работников, занятых в n-ой отрасли.
Очевидно, xi ≥ 0, i = 1, ..., n. Множество всевозможных наборов (x1, x2, ..., xn) обозначим 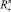 , т. е.
, т. е. 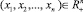 .
.
Предположим, что на 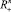 определена (например, методами регрессионного анализа) функция u(x1, x2, ..., xn), характеризующая «полезность» набора (x1, x2, ..., xn) (функция полезности).
определена (например, методами регрессионного анализа) функция u(x1, x2, ..., xn), характеризующая «полезность» набора (x1, x2, ..., xn) (функция полезности).
Цель данной работы: используя статистические данные о трудовых ресурсах и экономических показателях некоторого региона предложить математическую модель распределения трудового потенциала по отраслям, позволяющую максимизировать u(x1, x2, ..., xn) на 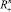 .
.
Согласно введенным обозначениям, требуемая модель имеет вид:
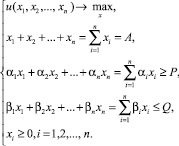 (1)
(1)
Задача оптимизации (1) является задачей нелинейного программирования. Для ее решения можно воспользоваться любой компьютерной программой статистической обработки данных (например, Excel, Statistica, Matlab).
Используем модель (1) для распределения трудового потенциала Ставропольского края по отраслям его экономики, согласно [5], в крае выделятся следующие отрасли, представленные в табл. 1.
Таблица 1
Распределение численности занятого населения Ставропольского края по видам экономической деятельности за 2009 год, тысяч человек[1]
|
№ п/п |
Всего занято в экономике |
799,2 |
|
в том числе: |
||
|
1 |
Добыча полезных ископаемых |
4,1 |
|
2 |
Обрабатывающие производства |
148,3 |
|
3 |
Производство и распределение электроэнергии, газа и воды |
36,9 |
|
4 |
Строительство |
87,3 |
|
5 |
Оптовая и розничная торговля; ремонт автотранспортных средств, мотоциклов, бытовых изделий |
218,1 |
|
6 |
Гостиницы и рестораны |
25,7 |
|
7 |
Транспорт и связь |
93,6 |
|
8 |
Финансовая деятельность |
13,4 |
|
9 |
Операции с недвижимым имуществом, аренда и предоставление услуг |
54,8 |
|
10 |
Безработные |
117,0 |
В табл. 2 представлены результаты затрат предприятий и организаций Ставропольского края на рабочую силу в 2009 году по выбранным отраслям экономики.
Таблица 2
Затраты предприятий и организаций на рабочую силу в 2009 году, рублей (по обследуемому кругу предприятий, рублей в расчете на одного работника в год)
|
№ п/п |
Всего по обследуемым видам деятельности |
2037621,6 |
|
в том числе: |
||
|
1 |
Добыча полезных ископаемых |
246501,6 |
|
2 |
Обрабатывающие производства |
201170,4 |
|
3 |
Производство и распределение энергии, газа и воды |
198495,6 |
|
4 |
Строительство |
185923,2 |
|
5 |
Оптовая и розничная торговля, ремонт автотранспортных средств |
162267,6 |
|
6 |
Гостиницы и рестораны |
103820,4 |
|
7 |
Транспорт и связь |
273952,8 |
|
8 |
Финансовая деятельность |
401944,8 |
|
9 |
Операции с недвижимым имуществом, аренда и предоставление услуг |
228745,2 |
|
10 |
Безработные |
2900 |
Из представленных данных следует, что в (1) Q = 2037621,6 рублей.
В табл. 3 представлены финансовые результаты предприятий и организаций Ставропольского края в 2009 году по выбранным отраслям экономики.
Таблица 3
Финансовый результат деятельности организаций по видам экономической деятельности за 2009 год, млн рублей
|
№ п/п |
Всего по обследуемым видам деятельности |
250235,3 |
|
в том числе: |
||
|
1 |
Добыча полезных ископаемых |
2211,6 |
|
2 |
Обрабатывающие производства |
34541,0 |
|
3 |
Производство и распределение электроэнергии, газа, тепловой энергии, воды |
17000,3 |
|
4 |
Строительство |
20155,7 |
|
5 |
Оптовая и розничная торговля, ремонт автотранспорта, бытовых изделий и предметов личного пользования |
57460,6 |
|
6 |
Деятельность гостиниц и ресторанов |
5185,2 |
|
7 |
Транспорт и связь |
30616,4 |
|
8 |
Финансовая деятельность |
65431,6 |
|
9 |
Операции с недвижимым имуществом, аренда и предоставление услуг |
17632,9 |
|
10 |
Безработные |
0 |
Из представленных данных следует, что в (1) P = 250235,3 млн рублей.
Рассчитаем значения коэффициентов αi и βi (см. табл. 4, 5).
Таблица 4
Значения αi на одного человека в рублях
|
α1 |
α2 |
α3 |
α4 |
α5 |
α6 |
α7 |
α8 |
α9 |
α10 |
|
539414,6 |
232913 |
460712,7 |
230878,6 |
263459,9 |
201758,8 |
327098,3 |
4882955 |
321768,2 |
0 |
Таблица 5
Значения βi в (1)
|
β1 |
β2 |
β3 |
β4 |
β5 |
β6 |
β7 |
β8 |
β9 |
β10 |
|
246501,6 |
201170,4 |
198495,6 |
185923,2 |
162267,6 |
103820,4 |
273952,8 |
401944,8 |
228745,2 |
2900 |
Экономико-математическая модель (1) оптимального распределения трудового потенциала Ставропольского края будет иметь вид:
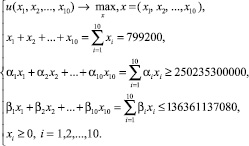 (2)
(2)
где αi и βi представлены в табл. 4 и 5 соответственно. В качестве целевой функции u(x1, x2, ..., x10) в (2) выберем функцию
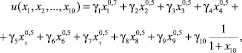 (3)
(3)
где 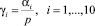 , вычисляются по данным табл. 3 и приведены в табл. 6.
, вычисляются по данным табл. 3 и приведены в табл. 6.
Таблица 6
Значения γi
|
γ1 |
γ2 |
γ3 |
γ4 |
γ5 |
γ6 |
γ7 |
γ8 |
γ9 |
γ10 |
|
0,00884 |
0,13803 |
0,06794 |
0,08055 |
0,22963 |
0,02072 |
0,12235 |
0,26148 |
0,07047 |
0,00000 |
Решив задачу нелинейного программирования (2), (3), найдем x1 = 44072, x2 = 104152, x3 = 17043, x4 = 31720, x5 = 227730, x6 = 1519, x7 = 78220, x8 = 274892, x9 = 19852, x10 = 0. При этом максимальный суммарный доход составит 1 497 770 060 296 рублей.
Таким образом, для получения максимального суммарного дохода в размере 1 497 770 060 296 рублей при заданных ресурсах необходимо запланировать количество трудовых ресурсов по отраслям в соответствии с указанными значениями xi.
Рецензенты:
Гурнович Т.Г., д.э.н., профессор кафедры финансового менеджмента и банковского дела, Ставропольский государственный аграрный университет, г. Ставрополь;
Калмыков И.А., д.т.н., профессор, заместитель директора по научной работе института информационных технологий и телекоммуникаций, ФГАОУ ВПО «Северо-Кавказский федеральный университет», г. Ставрополь.
Работа поступила в редакцию 04.06.2013.
[1] По 2009 г. включительно занятое население учитывалось по фактическому виду деятельности, начиная с 2010 г., распределение численности занятого населения осуществляется по основному виду деятельности организации
Библиографическая ссылка
Зайцева И.В., Зайцева И.В., Семенчин Е.А., Гимбицкий В.А. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОПТИМАЛЬНОГО РАСПРЕДЕЛЕНИЯ ТРУДОВОГО ПОТЕНЦИАЛА РЕГИОНА ПО ОТРАСЛЯМ ЭКОНОМИКИ // Фундаментальные исследования. 2013. № 8-2. С. 413-416;URL: https://fundamental-research.ru/ru/article/view?id=31934 (дата обращения: 15.02.2026).



