Разработка электрохимических процессов и технологических режимов абразивной активации и анодного удаления дефектного слоя с поверхности зеркал лучеводов на финишных операциях вибрационным электрохимическим хонингованием (ВЭХХ) (при вибрации и вращении катода-инструмента (КИ)) является важной задачей. Математически эта задача сводится к решению системы нелинейных уравнений типа
F(x) = y, (1)
где x – вектор искомых технологических параметров; y – вектор, определяющий заданную форму рефлектора зеркала; F – неявно заданное отображение, определяемое моделью процесса ЭХРО.
Изменение параметров процесса электрохимической размерной обработки (ЭХРО) в межэлектродном канале и абразивного механического удаления анодных пленок описывается системой уравнений переноса для одномерной модели в квазистатическом приближении при вибрации катода-инструмента (КИ) и его вращении с числом оборотов n с учетом влияния движения КИ на динамические характеристики электролита в межэлектродном промежутке (МЭП) и его температуру [2].
Система уравнений может включать:
1. Уравнение переноса массы:
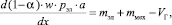 (2)
(2)
где α – газосодержание; w – объемный расход электролита; pэл – плотность электролита на входе в межэлектродный зазор; a – величина межэлектродного зазора.
Масса металла и анодных пленок, удаленных с поверхности зеркала лучевода абразивным механическим способом нетокопроводящими секторами КИ, может быть представлена выражением:
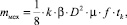 (3)
(3)
где β – центральный угол токоизолированного сектора с абразивным покрытием; k – количество токоизолированных секторов; D ‒ диаметр КИ; μ – величина массы металла и анодной пленки, срезанные за 1 секунду единицей площади токоизолированного сектора с абразивным покрытием; f – частота вибрации; tk – общее время контакта КИ и детали за 1 секунду процесса обработки.
Массу металла, аноднорастворенную при электрохимической обработке токопроводящими секторами КИ, можно рассчитать по формуле
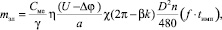 (4)
(4)
где Cме – электрохимический эквивалент растворения металла детали; γ – удельный вес металла детали; η – выход металла по току; U – рабочее расположение; Δφ – сумма анодного и катодного потенциалов; χ – удельная электропроводность электролита; n – число оборотов; tимп – время импульса технологического тока.
Масса выделенного водорода в межэлектродном промежутке определяется из выражения:
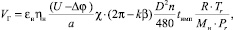 (5)
(5)
где εн – весовой электрохимический эквивалент водорода; ηн – коэффициент выхода по току при выделении водорода; R – универсальная газовая постоянная; Tr – абсолютная температура газожидкостной смеси; Pr – давление в газожидкостном слое; Mн – молекулярный вес водорода.
Уравнение переноса массы газа определим:
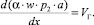 (6)
(6)
Время действия импульса технологического тока определяется:
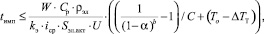
где C – температурный коэффициент электропроводности; b – показатель степени, обычно b = 1,5; To– температура электролита на входе в межэлектродный зазор; ΔTT – повышение температуры электролита в межэлектродном промежутке за счет силы трения при вращении КИ; Sэл.акт – площадь электропроводных секторов катода инструмента; kэ – коэффициент, учитывающий ту часть мощности электрического тока, которая тратится на нагрев.
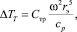
где Сср – коэффициент трения диска КИ о слой электролита в МЭП; ω – частота вращения КИ; Ср – теплоемкость электролита; rэ – радиус КИ.
2. Уравнение переноса энергии:
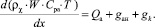 (7)
(7)
Плотность теплового потока за счет прохождения электрического тока и механического воздействия при вращении:
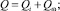 (8)
(8)
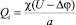 – плотность теплового потока при прохождении электрического тока, где Ср – теплоемкость электролита; Т – температура электролита; Q – средняя объемная плотность теплового потока при прохождении рабочего тока через МЭП.
– плотность теплового потока при прохождении электрического тока, где Ср – теплоемкость электролита; Т – температура электролита; Q – средняя объемная плотность теплового потока при прохождении рабочего тока через МЭП.
Где χ – удельная электропроводность электролита; U – напряжение на электродах; Δφ – сумма анодного и катодного потенциалов.
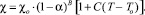 (9)
(9)
Тепловые потоки с поверхности катода и анода.
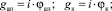 (10)
(10)
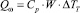 – плотность теплового потока электролита при вращении КИ.
– плотность теплового потока электролита при вращении КИ.
3. Уравнение изменения количества движения:
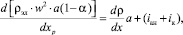 (11)
(11)
где p – давление в зоне обработки; iан, iк – касательные напряжения на аноде и катоде.
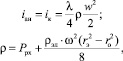 (12)
(12)
где ω – частота вращения КИ; rэ– радиус КИ; rо– радиус отверстия КИ на входе в МЭП.
Для ламинарного режима 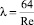 , для турбулентного режима
, для турбулентного режима
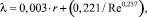
где число Рейнольдса 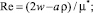
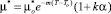 – динамическая вязкость среды, при То и αо = 0, m = 0,019; k = 5,5;
– динамическая вязкость среды, при То и αо = 0, m = 0,019; k = 5,5; 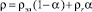 – плотность газожидкостной смеси в МЭЗ.
– плотность газожидкостной смеси в МЭЗ.
4. Уравнение изменения межэлектродного зазора:
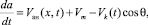 (13)
(13)
где Vан, Vm, Vk – скорости анодного растворения анода, абразивного механического удаления продуктов пленочного образования и подачи КИ; Vk = af, где f – частота вибрации привода; θ – угол между вектором скорости и нормалью к обрабатываемой поверхности.
Для канала (рис. 1) требуется найти распределение параметров процесса ВЭХХ по длине межэлектродного зазора (МЭЗ) α(х), D(х), Т(х), χ(х), ρг(х), ρ(х), α(х) и определить требуемый профиль КИ (рис. 2). Граничные условия для данной задачи следующие: заданы давление электролита на входе в канал Po и на выходе из канала P10, газосодержащие α, температура на входе в канал To, частота вращения КИ ω и вибрации f, амплитуда αo. Расчет распределения параметров по длине канала и изменение межэлектродного зазора проводилась численным методом Эйлера [1]. Для нахождения скорости подачи электролита на входе в канал использовался метод секущих [3].
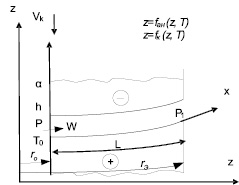
Рис. 1. Расчетная схема параметров формообразования ЭХРО по длине межэлектродного канала
В задачу расчета параметров ВЭХХ зеркала лучевода входило: определение профиля КИ, скорости его подачи, напряжение на электродах, давление и температура электролита на входе и на выходе из межэлектродного зазора, частоты вибрация и вращение КИ.
Вектор искомых параметров:
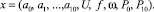 (14)
(14)
Необходимая форма профиля зеркала, заданная чертежом 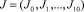 , а отображение F(x) есть форма обрабатываемой поверхности при заданной форме КИ и технологических параметрах
, а отображение F(x) есть форма обрабатываемой поверхности при заданной форме КИ и технологических параметрах
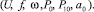 (15)
(15)
Заданная задача может иметь множество технологических параметров обработки, поэтому ее можно заменить следующей экстремальной задачей: найти вектор, при котором достигается величина
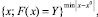 (16)
(16)
где x0 – вектор наиболее рациональной технологии, обеспечивающий оптимальную точность, производительность и качество поверхности. Здесь 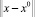 – евклидова норма вектора x – x0, т.е.
– евклидова норма вектора x – x0, т.е.
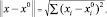 (17)
(17)
где 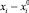 – координаты векторов x и x0 соответственно.
– координаты векторов x и x0 соответственно.
Предполагая, что функционал невязки выпуклый 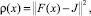 рекомендуется искать решение задачи (15) методом невязки, т.е. методом минимизации по функционалу.
рекомендуется искать решение задачи (15) методом невязки, т.е. методом минимизации по функционалу.
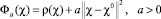 . (18)
. (18)
Выбор параметра регуляции α проводится по принципу невязки 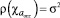 , где σ – уровень погрешности разностной схемы, реализующей систему дифференциальных уравнений на ЭВМ. Для минимизации функционала (17) применим метод Гаусса–Ньютона
, где σ – уровень погрешности разностной схемы, реализующей систему дифференциальных уравнений на ЭВМ. Для минимизации функционала (17) применим метод Гаусса–Ньютона
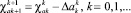 (19)
(19)
Одновременно с изменением номера итераций меняется параметр ak. В векторном равенстве (18) вектор поправок 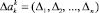 является решением системы уравнений
является решением системы уравнений
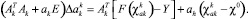 (20)
(20)
А параметр ah измеряется по закону
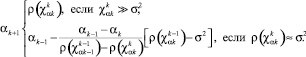 (21)
(21)
В формуле (15) 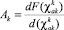 – матрица частных производных в точках
– матрица частных производных в точках 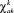 , вычисляемая по разностным формулам.
, вычисляемая по разностным формулам.
Система уравнений (21) решается с помощью вычислительной схемы [1], использующей перерасчеты факторизации Холецкого [3]. Итерационный процесс (20) прекращается, когда поправки для ak и χak становятся достаточно малыми. С использованием дифференциальных уравнений (1)–(12) и представленного метода производился расчет параметров ВЭХХ и профиля катода-инструмента для чистовой обработки зеркала лучевода из сплава 32 НДК. Проверка методики расчета проводилась путем расчета и экспериментального распределения съема металла для криволинейного канала, как и в работе [2]. При решении задачи формообразования необходимо было обеспечить равномерный съем на глубину 0,2 мм дефектного слоя зеркала лучевода, полученного после механической обработки лезвийным инструментом на станке с ЧПУ. Зеркало представляло собой вырезку цилиндром Ø128 мм из параболоида вращения:
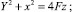 (22)
(22)
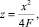
где F = 150 мм – фокусное расстояние.
Расчетные координаты x и z зеркала представлены в таблице.
Расчетные координаты зеркала
|
x, мм |
242,7 |
252 |
262 |
272 |
282 |
292 |
|
z, мм |
98,17 |
105,84 |
114,406 |
123,306 |
132,54 |
142,1 |
|
x, мм |
300 |
302 |
312 |
322 |
332 |
342 |
|
z, мм |
150 |
152,006 |
162,2 |
172,806 |
183,706 |
194,94 |
Отклонение рабочей поверхности зеркала от теоретической поверхности параболоида должно быть не более 0,05 мм, шероховатость поверхности Ra ≤ 0,8 мкм. В связи с отмеченным невязка при расчете была в пределах ±10–12 мм. Максимальная длина межэлектродного канала составляла 92 мм, минимальная – 70 мм. Наличие межэлектродного канала большой длины при ЭХРО обычно приводит к существенному влиянию газовыделения и перегрева электролита на равномерность съема металла по зазору и точность обработки. Для устранения указанных недостатков была разработана специальная конструкция катода-инструмента [4], метод электрохимического хонингования [5] и произведен расчет его рабочего профиля, а также параметров процесса с учетом уравнений (1)–(22) [6]. Для решения указанной задачи были разработаны алгоритм (рис. 3) и программа. Уточнение формы КИ проведено с варьированием U, Vk, Pвх, ω, f, W, что позволило получить распределение съема по зазору металла в пределах допуска с максимальной шероховатостью поверхности Ra = 0,2 мкм. Расхождение теоретических и экспериментальных данных на практике по съему в пределах 6,5–8 % позволило изготовить зеркала лучеводов с размеростабильными параметрами из сплава 32 НКД с требуемой точностью и шероховатостью поверхности (отклонения поверхности от теоретической не более 0,05 мм, шероховатость Ra = 0,16–0,2 мкм).
Разработанная модель позволяет рассчитать с применением ЭВМ профиль КИ и технологические параметры ВЭХХ в зависимости от геометрических размеров поверхности зеркала, заданных чертежом, и времени обработки. Разработанные алгоритм и программа могут быть использованы для создания метода ВЭХХ зеркал лучевода и других деталей АФУ с автоматизированным управлением. Учет технологических параметров процесса позволит управлять скоростями подачи, вращения, а также и частотой вибрации КИ, напряжением на электродах, температурой и давлением подачи электролита при ВЭХХ.
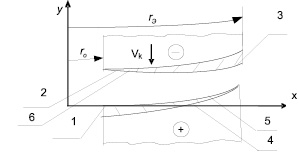
Рис. 2. Расчетная схема профиля катода-инструмента:1 – требуемый профиль обрабатываемой поверхности по чертежу; 2 – первоначальный профиль катода-инструмента; 3 – уточненный профиль катода – инструмента; 4 – полученный профиль детали; 5 – невязка (погрешность между полученным профилем детали и требуемым по чертежу); 6 – корректировка катода-инструмента
На основании поведенных теоретических исследований разработаны обобщенная модель для расчета распределения параметров процесса снижения шероховатости по поверхности зеркала лучеводов вибрационным электрохимическим хонингование и профиля катода-инструмента.
Определены способы решения технологической задачи путем ее замены экстремальной задачей и выбором параметров регуляризации по методу невязки, т.е. минимизации по χ функционала.
Предложены методы решения дифференциальных уравнений для определения параметров формообразования при ВЭХХ, разработан алгоритм расчета профиля катода-инструмента и распределения параметров процесса по длине межэлектродного канала.
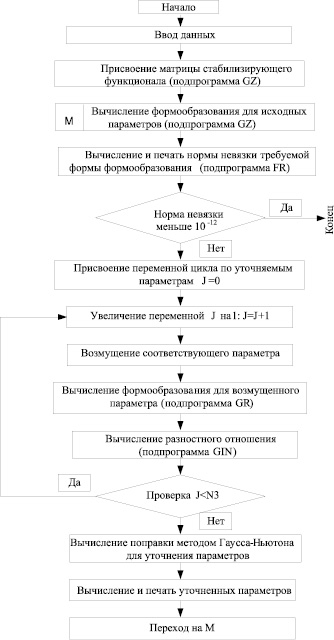
Рис. 3. Алгоритм расчета профиля катода-инструмента и распределения параметров по длине межэлектродного зазора
Рецензенты:
Шиманский А.Ф., д.х.н., профессор, заведующий кафедрой «Композиционные материалы и физикохимия металлургических процессов», Красноярский институт цветных металлов, г. Красноярск:
Кишкин А.А., д.т.н., профессор, заведующий кафедрой «Холодильная, криогенная техника и кондиционирование» Сибирского государственного аэрокосмического университета имени академика М.Ф. Решетнева, г. Красноярск.
Работа поступила в редакцию 06.06.2013.
Библиографическая ссылка
Оборина Л.И., Трифанов И.В., Рыжов Д.Р., Исмаылов Б.Н., Берсенев С.М. РАСЧЕТ ПАРАМЕТРОВ ПРОЦЕССА УДАЛЕНИЯ ДЕФЕКТНОГО СЛОЯ С РАБОЧЕЙ ПОВЕРХНОСТИ ЗЕРКАЛ ЛУЧЕВОДОВ ВИБРАЦИОННЫМ ЭЛЕКТРИЧЕСКИМ ХОНИНГОВАНИЕМ // Фундаментальные исследования. 2013. № 8-2. С. 295-301;URL: https://fundamental-research.ru/ru/article/view?id=31912 (дата обращения: 15.02.2026).



