В процессе эксплуатации тепловой станции решаются две основные задачи минимизации затрат при производстве электроэнергии. Первая связана с соблюдением оптимального текущего режима при фиксированном составе основного оборудования. Вторая – с необходимостью планирования перспективного развития, направленная на наращивание мощностей за счет ввода в работу новых агрегатов. При решении данных задач интерес представляют возможности и объемы используемых ресурсов, необходимых для производства энергии.
В качестве математической модели рассматривается производственная функция с зависимой переменной Р (значение активной мощности) и зависимых переменных В (затрачиваемое топливо) и К (основные средства). Тогда функция Р будет иметь вид: 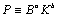 , где
, где ![]() и
и ![]() – положительные параметры, которые предстоит оценить, например, с помощью нелинейного метода наименьших квадратов. Решение поставленной задачи может быть реализовано как на оперативном, так и на перспективном уровне.
– положительные параметры, которые предстоит оценить, например, с помощью нелинейного метода наименьших квадратов. Решение поставленной задачи может быть реализовано как на оперативном, так и на перспективном уровне.
Для решения задачи «затраты – выпуск» на оперативном уровне представим функцию Р в виде ![]() , где
, где ![]() – затраты, связанные с расходом топлива и приобретением основных средств соответственно. Индекс
– затраты, связанные с расходом топлива и приобретением основных средств соответственно. Индекс ![]() обозначает номер агрегата станции. Поскольку выпуск электроэнергии меняется каждый час, то в динамике
обозначает номер агрегата станции. Поскольку выпуск электроэнергии меняется каждый час, то в динамике ![]() , где
, где 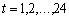 . Поскольку в процессе оперативной работы основные средства практически остаются неизменными, функцию Р можно представить как
. Поскольку в процессе оперативной работы основные средства практически остаются неизменными, функцию Р можно представить как
![]() , (1)
, (1)
где ![]() – положительный параметр, учитывающий наличие основных средств. С учетом того, что функция (1) исходит из нуля, а расходная характеристика должна учитывать ограничение условий работы агрегата, а именно: недопустимости выдачи электроэнергии на холостом ходу (
– положительный параметр, учитывающий наличие основных средств. С учетом того, что функция (1) исходит из нуля, а расходная характеристика должна учитывать ограничение условий работы агрегата, а именно: недопустимости выдачи электроэнергии на холостом ходу (![]() ) и перегрузочной способности блока (
) и перегрузочной способности блока (![]() ), сдвинем (1) в системе координат Охр:
), сдвинем (1) в системе координат Охр:
![]() (2)
(2)
Прибыль от работы ТЭС образуется как разность доходов от реализации электроэнергии и затратами на топливо. Тогда задача поиска эффективного использования оборудования будет иметь вид:
![]() (3)
(3)
при условии, что
![]() ,
,
![]() , (4)
, (4)
где ![]() тариф на отпущенную электроэнергию ТЭС;
тариф на отпущенную электроэнергию ТЭС; ![]() стоимость единицы топлива;
стоимость единицы топлива; ![]() спрос на электроэнергию.
спрос на электроэнергию.
Если хотя бы один ресурс не затрачивается агрегатом, т.е. ![]() или
или ![]() , объем выпуска продукции будет равен нулю, т.е.
, объем выпуска продукции будет равен нулю, т.е. ![]() . Тогда задача оптимизации представляет задачу на глобальный максимум (при
. Тогда задача оптимизации представляет задачу на глобальный максимум (при ![]() ). Точки локального абсолютного максимума
). Точки локального абсолютного максимума ![]() находятся среди решений системы уравнений
находятся среди решений системы уравнений ![]() . Вторые частные производные суммарной производственной функции
. Вторые частные производные суммарной производственной функции ![]() из (3) таковы, что
из (3) таковы, что ![]() . Отсюда следует, что суммарная функция
. Отсюда следует, что суммарная функция ![]() на
на ![]() представляет собой выпуклую вверх гиперповерхность. Решение (3) с учетом ограничений (4) может быть найдено с помощью метода неопределенных множителей Лагранжа. Представленная математическая модель позволяет определить оптимальную величину затрат ресурсов по каждому блоку станции при ее работе в краткосрочном периоде.
представляет собой выпуклую вверх гиперповерхность. Решение (3) с учетом ограничений (4) может быть найдено с помощью метода неопределенных множителей Лагранжа. Представленная математическая модель позволяет определить оптимальную величину затрат ресурсов по каждому блоку станции при ее работе в краткосрочном периоде.
Оптимизация затрат на ТЭС может быть достигнута и при помощи рационального (оптимального) распределения фонда оплаты труда между категориями работников. Задача состоит в оптимизации функции эффективности производства ![]() , где
, где ![]() скалярная функция векторного аргумента,
скалярная функция векторного аргумента, ![]() вектор параметров,
вектор параметров, ![]() ошибка аппроксимации. Аргументами функции эффективности
ошибка аппроксимации. Аргументами функции эффективности ![]() являются пропорции в распределении средней зарплаты между категориями работающих.
являются пропорции в распределении средней зарплаты между категориями работающих.
Доля средней зарплаты работников ![]() ой категории равна
ой категории равна ![]() , где
, где ![]() число категорий,
число категорий, ![]() – средняя зарплата
– средняя зарплата ![]() ой категории,
ой категории, ![]() – фактическая оплата труда работников
– фактическая оплата труда работников ![]() ой категории,
ой категории, ![]() численность
численность ![]() ой категории.
ой категории.
Пусть предприятие имеет возможность увеличить в году ![]() фонд оплаты на величину
фонд оплаты на величину ![]() . Задача состоит в ее оптимальном распределении по критериям, т.е. в определении величины
. Задача состоит в ее оптимальном распределении по критериям, т.е. в определении величины ![]() .
.
В соответствии с ранее введенными переменными имеем соотношения:
![]() (1)
(1)
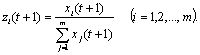 (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
Итак, задача состоит в поиске значений переменных ![]() , минимально отстоящих от чисел
, минимально отстоящих от чисел ![]() – оптимального значения доли средней зарплаты работников
– оптимального значения доли средней зарплаты работников ![]() ой категории в суммарной средней зарплате всего персонала:
ой категории в суммарной средней зарплате всего персонала:
![]() (6)
(6)
Задача нелинейного программирования (1)–(6) после некоторых упрощений может быть сведена к задаче линейного программирования. Пусть, например, известно не только приращение ![]() , но и новое в год
, но и новое в год ![]() – значение суммы средних зарплат по категориям
– значение суммы средних зарплат по категориям ![]() . С учетом этого уравнение (2) преобразуется к виду
. С учетом этого уравнение (2) преобразуется к виду ![]() . Далее изменим квадратичную форму (6) на сумму с модулем (изменим метрику):
. Далее изменим квадратичную форму (6) на сумму с модулем (изменим метрику): ![]() . При помощи введения новых переменных
. При помощи введения новых переменных ![]() этот кусочно-линейный функционал сводится к линейному:
этот кусочно-линейный функционал сводится к линейному: ![]() . Таким образом, задача поиска оптимальных значений переменных
. Таким образом, задача поиска оптимальных значений переменных ![]() сводится к задаче линейного программирования, методы решения которой известны.
сводится к задаче линейного программирования, методы решения которой известны.
СПИСОК ЛИТЕРАТУРЫ:
1. Автоматное управление асинхронными процессами в ЭВМ и дискретных системах (под редакцией В.И. Варшавского). М.: Наука, 1986.
2. Носков С.И., Ким В.Х. Математическое моделирование влияния структуры фонда оплаты труда на эффективность производства. Иркутск: ВСИ МВД РФ, 2000.
3. Носков С. И. Технология моделирования объектов с нестандартным функционированием и неопределенностью в данных. – Иркутск: «Облинформпечать», 1996.
Библиографическая ссылка
Ермилова Н.А. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЭКОНОМИЧЕСКИ ВЫГОДНОЙ РАБОТЫ ТЕПЛОВОЙ СТАНЦИИ // Фундаментальные исследования. 2007. № 6. С. 61-63;URL: https://fundamental-research.ru/ru/article/view?id=3171 (дата обращения: 07.03.2026).



