Экструзия электродных покрытий из керамической пластифицированной электродообмазочной массы на металлический электродный стержень широко известна и достаточно подробно изучена [1, 2].
Однако необходимость малотоннажного производства специальных покрытых электродов различной номенклатуры и назначения требует знания научно-обоснованных рекомендаций по подготовке и переработке пластифицированных электродообмазочных масс, разработки методик оценки их реологических характеристик, разработки режимно-конструктивных параметров комплекса технологического оборудования для таких производств.
Технологические свойства электродообмазочных масс в значительной мере зависят от характеристики связующего компонента (в нашем случае водный раствор жидкого стекла), гранулометрического состава компонентов сварочных материалов, соотношения заданного состава компонентов и связующего в пластифицированной электродообмазочной массе.
В процессах экструзии электродных покрытий на металлический стержень осуществляется течение пластифицированной массы в каналах различной формы. Реологические свойства такой массы по-разному проявляются в зависимости от геометрии потока. Знание реологических свойств электродообмазочной массы позволяет сформировать условия, необходимые для получения электродного покрытия с заданным уровнем технологических свойств.
В настоящее время существует несколько типов приборов для оценки реологических свойств [3]. К ним относятся ротационные приборы с рабочими узлами типа конус-плоскость, с коаксиальными цилиндрами, параллельными пластинами, а также капиллярные и трубчатые вискозиметры. Методы капиллярной и трубчатой вискозиметрии для определения кривых течения оказываются удобнее и проще методов ротационной вискозиметрии. Капиллярные и трубчатые системы позволяют оценить пристенные и ориентационные эффекты и, кроме того, они являются простейшими модельными системами, в которых поле наполнений и скоростей деформации неоднородно, а кинематика течения наиболее проста.
На основе анализа картин течения в капилляре была разработана методика и капиллярный вискозиметр определения реологических характеристик пластифицированных керамических электродообмазочных масс [4, 5].
Основа методики [6] базируется на том, что течение пластифицированной массы в капилляре рассматривается как простой сдвиг жидкости при установившемся ламинарном изотермическом течение в капилляре постоянного течения и бесконечной длины с учетом «входовых», «концевых» и «пристеночных» эффектов.
Кривые течения (зависимости напряжения сдвига от скорости сдвига) как характеристика исследуемого материала устанавливаются путем измерения перепада давления по длине капилляра и определения скорости течения.
На рис. 1 схематически показаны изменения перепадов давления в резервуаре и в капилляре. Общий перепад давления между точкой в верхней части вискозиметричеокого резервуара и областью выхода из трубы состоит из 3-х слагаемых:
ΔР = ΔРвх + ΔРкап + ΔРвых. (1)
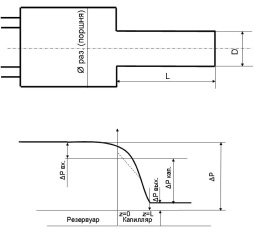
Рис. 1. Схема распределения давления в резервуаре и в капилляре
Для вязкоупругих жидкостей общий перепад давления на входе в капилляр ΔРвх можно условно разделить на две составляющие: вязкую ΔРвязк и высокоэластичную ΔРэл.
ΔРвх = ΔРвязк + ΔРэл. (2)
Так как ΔРвязк составляет менее 5 % от общего значения, то практически можно полагать:
ΔР = ΔРэл. (3)
ΔРвх определяется только скоростью сдвига и практически не зависит от отношения L/D. Бегли [7] полагал, что высокие значения перепада давления на входе в капилляр можно рассматривать как фиктивное увеличение длины капилляра, а также при фиксированной скорости сдвига зависимость общего падения давления от отношения длины капилляра к его диаметру должна быть линейной. Такие зависимости часто называют зависимостями по Бегли (рис. 2). Экстраполяция этих позиций к нулевому давлению дает отношение фактического значения длины капилляра к его диаметру при определенной скорости сдвига.
Исходя из этого, Бегли предложил следующее уравнение для расчета истинного напряжения сдвига на стенке капилляра τW:
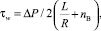 (4)
(4)
где ΔР – общая разность давлений в двух точках: в вискозиметрическом резервуаре и на выходе из капилляра; L/R – отношение длины капилляра к его радиусу; nв – входная поправка при фиктивном удлинения капилляра.
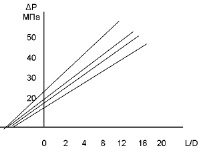
Рис. 2. Зависимость общего перепада давления от отношения длины капилляра к его диаметру при различных скоростях сдвига
Кривые течения как характеристики исследуемого материала не должны зависеть от геометрических параметров канала. Входовая поправка необходима для получения кривых течения, инвариантных относительно геометрических параметров капилляра.
Значение поправки nв можно определить, построив график зависимости ΔP = f/(L/R). Этот метод определения предполагает проведение измерений на нескольких капиллярах с различными отношениями L/R. Простейший прием учета входовых потерь требует использования двух капилляров разной длины (L1 и L2), но одинакового радиуса. Измерения на обоих капиллярах должны производиться при одинаковых расходах или пересчитываться как одинаковые расходы, тогда:
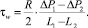 (5)
(5)
Уравнение течения жидкости для устойчивого течения с развившимся профилем скоростей (течение в капилляре) может быть записано в цилиндрических координатах:
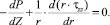 (6)
(6)
Интегрируется в пределах от r = 0 до произвольного r, получим:
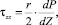 (7)
(7)
где dP/dZ градиент давления в области полностью развившегося течения, не зависит от r.
Напряжение сдвига на стенке τW (т.е. при r = R)
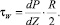 (8)
(8)
При течении ньютоновской жидкости из резервуара в капилляр с радиусом R и длинной L эффективную скорость сдвига γэф можно определить:
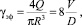 (9)
(9)
где Q – объемная скорость течения; V – средняя скорость течения жидкости; D – диаметр капилляра.
Объемная скорость течения Q может быть найдена из профиля скорости υz(r) в капилляре:
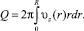 (10)
(10)
Принимая, что скольжение на стенке капилляра отсутствует, т.е. υz(r) = 0, интегрируется по частям с учетом предыдущих формул и имея для постоянной скорости сдвига dυz/dr = γ. Получим:
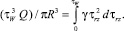 (11)
(11)
Дифференцируя и используя правило Лейбница:
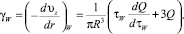 (12)
(12)
Поставим γэф уравнения (9) в (12):
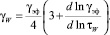 (13)
(13)
Это соотношение, впервые полученное Вайссенбергом [8], известно как уравнение Рабиновича-Муни и используется при расчете истинной скорости сдвига при течении ньютоновской жидкости.
С другой стороны, из экспериментальных данных хорошо известно, что для многих материалов зависимость τW = f(γэф) в двойных логарифмических координатах выражается прямой линией в достаточно широкой области значений γэф.
Можно записать эмпирическое уравнение:
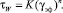 (14)
(14)
В этом уравнении n – угловой коэффициент графика зависимости lg τW = f(lg γэф):
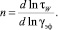 (15)
(15)
Тогда уравнение для γэф можно переписать:
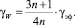 (16)
(16)
Подставив эту формулу в выражении для τW, получим:
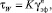 (17)
(17)
где К = К1∙[4n/(3n + 1)]n. (18)
При n = 1 эта формула сводится к выражению, описывающему течение ньютоновских жидкостей:
τW = Kγэф. (19)
где К – ньютоновская вязкость среды.
Можно сделать вывод, что значения n, отличные от 1, указывают на отклонение свойств материала от характеристики ньютоновской дикости. Уравнении τW = KγWn известно как степенной закон течения Оствальда-де-Вилла, а жидкости, ему подчиняющиеся, – «степенные».
Распределение скорости в капилляре для «степенной» жидкости определим, интегрируя:
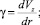
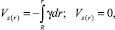 (20)
(20)
т.е. скольжение на стенке капилляра отсутствует.
Из дальнейших преобразований получим:
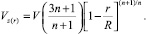 (21)
(21)
Таким образом, для построения кривой течения (зависимости напряжения сдвига от скорости сдвига) достаточно произвести измерение перепада давления по длине капилляра и определить скорость течения. С помощью уравнения (17) и кривых течения, встроенных в двойных логарифмических координатах, можно определить две реологические константы K и n в степенном законе течения: n – по углу наклона кривой; K – это τW, при γw = 1. Из кривых течения можно рассчитать также вязкость:
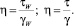 (22)
(22)
Для жидкости, подчиняющейся степенному закону, выражение для вязкости получим, подставив (17) в (22):
τW = Kγn – 1. (23)
Отсюда следует, что при n < 1 вязкость уменьшается с возрастанием скорости сдвига γ. Из литературы [9, 10] известно, что для ряда исследованных материалов вязкость остается постоянной при низкой скорости сдвига вплоть до определенного значения γ, а затем дальнейшее возрастание скорости сдвига вызывает снижение вязкости. При исследовании процессов течения систем могут проявляться пристенные и ориентационные эффекты, например, проскальзование на стенке. Результатом этих эффектов может быть значительное изменение граничных условий при течении материала. В результате проскальзывания наблюдается снижение эффективного радиуса по сравнению с номинальным радиусом измерительного угла (капилляра), который по обработке данных входит в расчетную формулу в третьей степени. Поэтому погрешность при определении кривой течения может быть существенной. При оценке влияния пристенного скольжения на результаты измерений в капиллярных вискозиметрах исходят из предположения, что скорость движения среды относительно стенки капилляра определяется скачком скорости в пристенном слое (Vск скорость скольжения), а также скоростью сдвига ламинарно пересекающихся слоев в объеме. Если Vск – однозначная функция напряжения сдвига, то средняя скорость сдвига γ определяется:
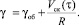 (24)
(24)
Измерение γ для капилляров с различными радиусами R при нескольких постоянных значениях позволяет определить функции течения γоб(τW) и скольжения Vск(τW) (метод Муни).
Реологические характеристики пластифицированной массы определяются в следующей последовательности:
1. Готовят набор капилляров следующих геометрических соотношений – L/D (L – длина капилляра, D – диаметр капилляра) (мм): 4/2, 8/2, 12/2, 20/2, 6/3, 12/3, 18/3, 30/3, 5/10, 5/20, 5/30, 5/50.
2. Для каждого капилляра проводят серию экспериментов пристеночных скоростей течения. Для этого рабочий узел, состоящий из капилляра и вискозиметрического резервуара с исходным материалом, териостатируют, затем материал подвергают нагружению при различных скоростях движения поршня . При этом для каждой скорости измеряют величину давления прессования. Далее для каждого капилляра соответствующей скорости поршня рассчитывают:
– давление Р по усилию F на прессе Р = F/S, где S – площадь поперечного сечения поршня или замеряют давление датчиками, установленными на капилляре;
– объемную скорость истечения Q (объемный расход в единицу времени)
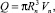 (25)
(25)
где Rn – радиус поперечного сечения поршня; Vn – скорость движения поршня. Если в качестве нагрузочного устройства используется шнек, то расход Q определяется в процессе экструзии, например, весовым способом. При этом объем истекающего из капилляра материала за единицу времени рассчитывается по формуле:
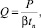 (26)
(26)
где Р – вес образца: β – удельный вес; tn – время выхода образца; эффективную скорость сдвига γэф при течении ньютоновской жидкости из резервуара в капилляр с радиусом R и длиной L:
γ = 40/πR3, (27)
где Q – объемная скорость течения.
3. Для расчета сдвиговых напряжений на стенке капилляра τW с учетом поправок на входные эффекты необходимо:
– построить график зависимости давления от эффективной скорости сдвига Р = f(γэф) для капилляров с различными геометрическими соотношениями, например: L/D = 2, 4, 6, 10;
– построить график зависимостей давления от геометрических параметров Р = f(L/D) при различных скоростях сдвига. Для этого, значения давления Р для различных соотношений L/D определяют по графику (рис. 3) при определенной скорости сдвига γэф. Например, кривая для γ1 (рис. 4) построена по точкам 1, 2, 3, 4 соответствующим аналогичным точкам графика (рис. 3). Таким образом, каждая кривая характеризует течение материала в капиллярах с разной геометрией при равных скоростях сдвига;
– рассчитать входовые («концевые») поправки (поправки по Бэгли nв или Рв). Для этого необходимо проэкстраполировать кривые гррафика зависимостей по Бегли (рис. 4) до нулевого значения. На оси давления отсекаются отрезки, равные Рв, а на оси L/D отрезки nв. Для учета «концевых» эффектов можно использовать любую из этих поправок, например, воспользуемся поправкой Рв и построим зависимость Рв от эффективной скорости скольжения γэф. Для этого с графика (рис. 4) снимают значения отрезков Рв, соответствующие различным скоростям сдвига;
– вычислить сдвиговые напряжения на стенке капилляра τw с учетом поправки, находя значения по графику (рис. 5) для любой (соответствующей нашему расчету) скорости сдвига γэф.
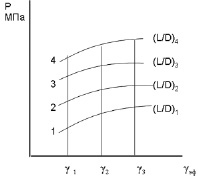
Рис. 3. Зависимость давления от эффективной скорости сдвига для капилляров с различными L/D
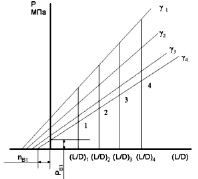
Рис. 4. Зависимость для определения входовых поправок
Построим кривую течения, т.е. зависимость напряжения сдвига на стенке капилляра τw от эффективной скорости сдвига γэф. Полученный график позволяет определить наличие эффектов скольжения. На рис. 6 приведены примеры:
а) проскальзывание материала на стенках капилляра отсутствует;
б) скольжение существенно, т.к. для капилляров с различными радиусами своя кривая течения τw = f(γэф).
При учете эффектов скольжения эксперимент необходимо провести на капиллярах с внутренней кольцевой нарезкой (глубина нарезки 1/50–1/100).
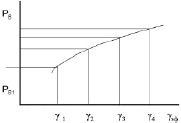
Рис. 5. Зависимость для определения сдвиговых напряжений с учетом поправки по Бегли
4. Для расчета вязкости материала, полагая, что поведение материала можно описать в рамках степенного закона (18) и построив кривую течения в двойных логарифмических координатах lg τw – lg (γэф) (рис. 7) находим:
– n – показатель степени в 18 – угловой коэффициент графика зависимостей lg τw – lg (γэф) (рис. 7).
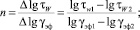 (28)
(28)
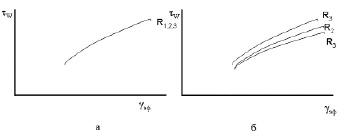
Рис. 6 Кривые течения при отсутствии проскальзывания (а) на стенках капилляра и при наличии скольжения (б)
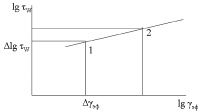
Рис. 7. Логарифмическая зависимость между сдвиговым напряжением и эффективной cкоростью сдвига
– γW – истинная скорость на стенке капилляра рассчитывается по формуле Рабиновича-Муни (13) с учетом (18):
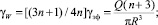 (29)
(29)
– К – константа в степенном уравнении (18) с учетом истинной скорости:
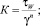 (30)
(30)
– рассчитать эффективную вязкость материала по формуле:
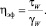 (31)
(31)
Для жидкости, подчиняющейся степенному закону, выражение для вязкости (18) имеет вид:
η = Kγn–1. (32)
Разработанный нами капиллярный вискозиметр устанавливался на разрывной машине Р5. Усилие передавалось через соответствующие динамометры сжатия.
Сухая смесь электродообмазочной массы готовилась из материалов постоянного гранулометрического состава, перемешивалась с дозой жидкого стекла (содержание стекла в обмазочной массе – 22 % мас; модуль – 2,54; плотность – 1,54 г/см3) в течение одного и того же промежутка времени (t = 12 мин) после чего у приготовленной массы одновременно были определены реологические характеристики, получены и исследованы образцы на прочность сырой обмазочной массы.
Анализ результатов показывает, что получение качественных электродных покрытий возможно при значениях сдвигающихся напряжений τСД массы в пределах 2–4∙104 Па, предел прочности на разрыв такой обмазочной массы составляет 0,36–0,44 кг/см2.
Рецензенты:
Беленький В.Я., д.т.н., профессор, зам. директора, Западно-Уральский аттестационный центр, г. Пермь;
Кривоносова Е.А., д.т.н., профессор, ведущий специалист, Западно-Уральский аттестационный центр, г. Пермь,
Работа поступила в редакцию 08.05.2013.
Библиографическая ссылка
Наумов С.В., Канина А.Е., Игнатова А.М., Игнатов М.Н. ОПРЕДЕЛЕНИЕ РЕОЛОГИЧЕСКИХ СВОЙСТВ ЭЛЕКТРОДООБМАЗОЧНЫХ МАСС НА ОСНОВЕ ГАББРО-ДИАБАЗОВ ДЛЯ ПРОИЗВОДСТВА СВАРОЧНЫХ ПОКРЫТЫХ ЭЛЕКТРОДОВ // Фундаментальные исследования. 2013. № 6-5. С. 1068-1074;URL: https://fundamental-research.ru/ru/article/view?id=31687 (дата обращения: 28.12.2025).



