Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Бараков В.С. 1

---

1 ФГБОУ ВПО «Волгоградский государственный университет»

В статье проводится анализ развития экономического потенциала макрорегионов с учетом модернизационных преобразований, в котором особое внимание уделяется трем существенным факторам, оказывающим влияние на величину валового регионального продукта: социально-экономический; инвестиционный и инновационный факторы. Для проведения моделирования экономического развития макрорегионов РФ используются эконометрические методы, такие как регрессионный и корреляционный анализ. В результате проведения анализа ведется построение линейных регрессионных моделей, показывающих зависимость валового регионального продукта от выделенных показателей признаков, отражающих сущность трех факторов. В работе проводится детальный анализ и проверка на значимость полученных уравнений регрессий и их коэффициентов. Разработанные модели экономического развития макрорегионов РФ позволяют оценивать и прогнозировать величину результирующего показателя – валового регионального продукта.

Статья в формате PDF

681 KB

экономическое развитие

оценка

инвестиции

регион

корреляционный анализ

регрессионный анализ

инновации

1. Буянова М.Э. Оценка риска социально-экономического развития регионов Юга России // Вестник Волгоградского государственного университета. Серия 3. Экономика. Экология. – 2012. – № 1(20). – С. 85–94.

2. Вуколов Э.А. Основы статистического анализа. Практикум по статистическим методам и исследованию операций с использованием пакетов STATISTICA и EXCEL: учебное пособие. – М.: ФОРУМ: ИНФРА-М, 2004. – С. 160.

3. Калинина А.Э., Калинина В.В. Многофакторная оценка состояния промышленности регионов Южного федерального округа (ЮФО) // Современные проблемы науки и образования. – 2012. – № 5. – URL: http://www.science-education.ru/105-6821.

4. Регионы России. Социально-экономические показатели. 2010: Стат. сб. / Росстат. - М. – Режим доступа http://www.gks.ru/bgd/regl/B05_14p/Main.htm.

5. Регионы России. Социально-экономические показатели. 2012: стат. сб. / Росстат. - М., 2012. - 990 с.

Тенденции развития экономического потенциала макрорегионов в значительной степени зависят от трех существенных факторов: во-первых, от социально-экономического положения региона; во-вторых, от тех инвестиций, которые будут осуществлены в регионах; в-третьих, от инноваций, которые разрабатываются и применяются в регионах. Для выявления процессов экономического развития в России в макрорегиональном срезе возможно также применение эконометрических методов анализа [1, 2, 3]. Особый интерес представляет оценка влияния факторов на величину валового регионального продукта в макрорегионе. Решение этой задачи требует определения результирующего показателя, характеризующего эффективность оценки потенциала модернизации экономического развития. В соответствии с методологическими пояснениями российского статистического ведомства валовой региональный продукт (ВРП) – обобщающий показатель экономической деятельности региона, характеризующий процесс производства товаров и услуг для конечного использования. ВРП рассчитывается в текущих основных ценах (номинальный объем ВРП), а также в постоянных ценах (реальный объем ВРП) [5]. Оценка уровня потенциала модернизации экономического развития в макрорегионах, входящих в состав РФ, является актуальной проблемой, поскольку выступает интегральной характеристикой и определяется достаточно большим множеством факторов. Построение такого показателя в рамках детерминированных моделей затруднительно, поэтому целесообразно построить систему линейных моделей множественной регрессии по трем выделенных группам факторов, составляющих потенциал модернизационных преобразований региона: социально-экономического, инвестиционного и инновационного. Зависимой, обобщающей переменной в данном случае будем использовать валовой региональный продукт на душу населения.

Многофакторная модель строится в соответствии с функциональной зависимостью типа:

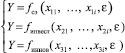(1)

Исходная система данных рассчитана по восьми макрорегионам России за 2000–2011 гг/ [4, 5]. На первом этапе проведем моделирование влияния социально-экономического фактора на результативный показатель «валовой региональный продукт на душу населения»:

Y = fсэ(x11, …, x18, ε), (2)

где Y – валовой региональный продукт на душу населения, тыс. руб.; х11 – уровень безработицы (%); х12 – среднедушевые денежные доходы населения (руб. в месяц); х13 – уровень экономической активности населения (%); х14 – индекс промышленного производства (в % к предыдущему году); х15 – удельный вес убыточных организаций (в % от общего числа организаций); х16 – степень износа основных фондов, %; х17 – численность населения с денежными доходами ниже величины прожиточного минимума (в % от общей численности населения субъекта); х18 – среднегодовая численность занятых в экономике (тыс. чел); ε – cлучайная составляющая.

Проведем анализ корреляционной зависимости 8 факторов, предположительно влияющих на итоговый показатель – валовой региональный продукт на душу населения. Корреляционная матрица независимых факторных признаков показывает, что они слабо коррелируют между собой, и поэтому с применением метода пошаговой регрессии появляется возможность построить значимую модель линейной регрессии (табл. 1).

Таблица 1

Корреляционная матрица независимых факторных признаков

Далее проводим ступенчатый отсев регрессоров. Процесс повторяется до тех пор, пока не останутся только значимые регрессоры. В результате получено уравнение множественной регрессии следующего вида:

Yсэ = –133,7 – 7,92х11 + 0,02х12 + +1,3х15 + 2,6х16 + 1,98х17 – 0,003х18. (3)

Коэффициенты регрессионной модели на заданном уровне значимы. Статистические оценки модели и ее параметров оказались полностью состоятельными (рис. 1). Коэффициент множественной корреляции показывает, что 96 % суммарной вариации результирующего показателя объясняется вариабельностью включенных в модель факторов.

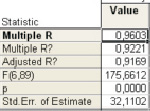
Рис. 1. Параметры оценки регрессионной модели

Где R – коэффициент множественной корреляции (описывает степень линейной зависимости между Y и факторами); F – F-статистика; p – вычисленный уровень значимости модели. О неслучайной природе полученных значений коэффициентов регрессии свидетельствуют их стандартные ошибки. В наших расчетах принят 5 %-й (р = 0,05 уровень вероятности ошибки. В модели расчетные значения стандартных ошибок для всех коэффициентов регрессии меньше задаваемого уровня. Проанализируем график остатков (рис. 2). Все остатки укладываются в симметричную относительно нулевой линии полосу шириной ±2S. Это означает, что дисперсии ошибок наблюдений постоянны.

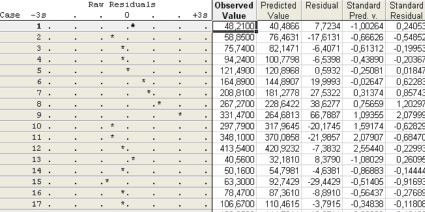
Рис. 2. График остатков

Теперь проверим гипотезу о нормальности распределения остатков. Результаты представлены на следующем графике (рис. 3). Из графика видно, что точки расположены близко к прямой, значит, можно предположить, что остатки распределены по нормальному закону. Таким образом, можно считать, что предположения регрессионного анализа выполняются.

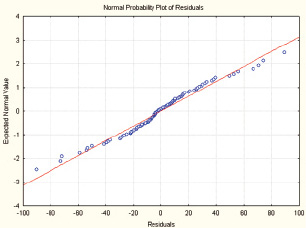
Рис. 3. Остатки на графике Normal Probability Plot

На втором этапе проведем моделирование влияния инвестиционного фактора на результативный показатель «валовой региональный продукт на душу населения»:

Y = fнвест(x21, …, x28, ε), (4)

где Y – валовой региональный продукт на душу населения, тыс. руб.; х21 – темп роста валового накопления основного капитала (%); х22 – доля инвестиции в основной капитал организаций с участием иностранного капитала (%); х23 – инвестиции в основной капитал на душу населения (тыс. руб); х24 – индекс физического объема инвестиций в основной капитал (в % к предыдущему году); х25 – удельный вес инвестиций в основной капитал в валовом региональном продукте; х26 – доля собственных средств в источниках финансирования инвестиций в основной капитал, %; х27 – доля банковских кредитов в привлеченных источниках финансирования инвестиций в основной капитал, %; х28 – доля бюджетных средств в привлеченных источниках финансирования инвестиций в основной капитал, %; ε – случайная составляющая.

Аналогично первому этапу проведем анализ корреляционной зависимости 8 факторов, предположительно влияющих на итоговый показатель – валовой региональный продукт на душу населения. Корреляционная матрица независимых факторных признаков показывает, что они слабо коррелируют между собой, и поэтому с применением метода пошаговой регрессии появляется возможность построить значимую модель линейной регрессии (табл. 2).

Таблица 2

Корреляционная матрица независимых факторных признаков

Далее снова проводим ступенчатый отсев регрессоров. В результате получаем уравнение множественной регрессии следующего вида:

Yинвест = 200,7 – 0,3х21 + 3,2х23 – – 5,3х25 – 0,7х26 + 3,2х27. (5)

Коэффициенты регрессионной модели на заданном уровне значимы. Коэффициент множественной корреляции показывает, что 96 % суммарной вариации результирующего показателя объясняется вариабельностью включенных в модель факторов. В модели расчетные значения стандартных ошибок для всех коэффициентов регрессии меньше задаваемого уровня. Все остатки укладываются в симметричную относительно нулевой линии полосу шириной ±2S. Это означает, что дисперсии ошибок наблюдений постоянны. Таким образом, предположения регрессионного анализа выполняются.

На последнем, третьем этапе проведем моделирование влияния инновационного фактора на результативный показатель «валовой региональный продукт на душу населения»:

Y = fиннов(x31, …, x38, ε), (6)

где Y – валовой региональный продукт на душу населения, тыс. руб.; x31 – число организаций, выполнявших научные исследования и разработки; x32 – численность персонала, занятого научными исследованиями и разработками (чел.); x33 – внутренние затраты на научные исследования и разработки (млн руб.); x34 – число созданных передовых производственных технологий; x35 – число используемых передовых производственных технологий; x36 – затраты на технологические инновации (млн. руб.); x37 – объем инновационных товаров, работ, услуг (млн руб.); ε – случайная составляющая.

Также проведем анализ корреляционной зависимости 8 факторов, предположительно влияющих на итоговый показатель – валовой региональный продукт на душу населения (табл. 3).

Таблица 3

Корреляционная матрица независимых факторных признаков

Далее проводим ступенчатый отсев регрессоров. В результате получено уравнение множественной регрессии следующего вида:

Yиннов = 117,7 – 0,08х31 + 0,0006х33 + + 0,002х36 – 0,0002х37. (7)

Коэффициенты регрессионной модели и параметры данного уравнения на заданном уровне значимы.

Таким образом, представим полную систему линейных регрессионных уравнений, отражающую влияние социально-экономического, инвестиционного и инновационного факторов на величину валового регионального продукта на душу населения:

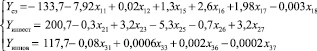(8)

Полученные уравнения множественной регрессии показывают высокую тесноту связи между динамикой валового регионального продукта по макрорегионам РФ и выделенными приоритетными признаками-показателями. Об этом свидетельствуют высокие значения полученных коэффициентов множественной корреляции, превышающие критический его уровень (0,7).

Заключение

По величине коэффициентов при факторных признаках уравнений регрессии представляется возможным выделить приоритеты изучаемых факторов по степени их влияния на результат валового регионального продукта. Положительное влияние на величину валового регионального продукта на душу населения оказали следующие факторы-признаки: рост среднедушевых денежных доходов населения; удельный вес убыточных организаций; величина износа основных фондов; численность населения с денежными доходами ниже величины прожиточного минимума; увеличение инвестиций в основной капитал на душу населения; рост доли банковских кредитов в привлеченных источниках финансирования инвестиций в основной капитал; увеличение внутренних затрат на научные исследования и разработки; увеличение затрат на технологические инновации; рост объема инновационных товаров, работ, услуг. Отрицательное влияние на величину валового регионального продукта на душу населения оказали следующие факторы-признаки: высокий уровень безработицы; среднегодовая численность занятых в экономике; доля инвестиции в основной капитал организаций с участием иностранного капитала, удельный вес инвестиций в основной капитал в валовом региональном продукте; доля собственных средств в источниках финансирования инвестиций в основной капитал; число организаций, выполнявших научные исследования и разработки. Таким образом, система уравнений линейной множественной регрессии, а также отмеченные выше статистически состоятельные оценки параметров модели показывают, что результат валового регионального продукта имеет высокую тесноту связи с выделенными приоритетными факторными признаками.

Рецензенты:

Мосейко В.О., д.э.н. профессор, директор института управления и региональной экономики, ФГАОУ ВПО «Волгоградский государственный университет», г. Волгоград;

Буянова М.Э., д.э.н., профессор кафедры мировой и региональной экономики, ФГАОУ ВПО «Волгоградский государственный университет», г. Волгоград.

Работа поступила в редакцию 07.05.2013.

Библиографическая ссылка