Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Трудов А.В. 1

---

1 ФГВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского»

Большинство научных работ по космической тематике [3, 6] направлено на исследование влияния технической компоненты системы эксплуатации РКТ на эффективность процесса подготовки ракет космического назначения (РКН) к применению. Исследованию влияния свойств расчетов, реализующих этот процесс, на показатели его эффективности уделялось значительно меньшее внимание. Научные работы, выполненные в этом направлении, посвящены в основном исследованию характеристик операторов, а не расчета в целом [4]. Исключение составляют работы, в которых исследуется влияние численности расчетов на характеристики процесса подготовки [2]. В статье предлагается метод формирования структуры расчетов подготовки РКН к пуску. В основу метода положена теоретико-множественная модель этого процесса, отображающая свойства персонала расчетов, которые непосредственно влияют на его результативность. В качестве показателя результативности принимается вероятность своевременного пуска РКН.

Статья в формате PDF

1038 KB

взаимозаменяемость

смежная специальность

отношение на множестве

фактор–множество

сечение множества

мультиграф

суграф

1. Вагнер Г., Основы исследования операций. – Т. 2. – М.: Мир, 1973. – 486с.

2. Волков Л.И. Методика оценки надежности ракетного комплекса в зависимости от численности обслуживающего личного состава // Двойные технологии. – 2001. – № 1. – С. 14–16.

3. Волков Л.И. Управление эксплуатацией летательных комплексов. – М.: Высшая школа, 1981. – 368 с.

4. Душков Б.А., Ломов Б.Ф., Смирнов Б.А. Хрестоматия по инженерной психологии. – М.: Высшая школа, 1991. – 287 с.

5. Калинин В.Н., Резников Б.А., Варакин Е.И. Теория систем и оптимального управления. Часть 1. – Л.: ВИКИ имени А.Ф. Можайского, 1979. – 319 с.

6. Северцев Н.А., Дедков В.К. Системный анализ и моделирование безопасности. – М.: Высшая школа, 2006. –464 с.

Многолетний опыт эксплуатации ракетно-космической техники показывает, что процесс подготовки (ПП) ракет космического назначения (РКН) и их составных частей к применению по назначению на космодромах продолжает оставаться длительным и трудоемким. Это обусловлено особенностями конструкции современных РКН и технологией подготовки их к пуску. Для подготовки РКН к пуску формируется расчет подготовки и пуска (РПП) РКН, состоящий из специалистов различных специальностей. Высокая цена неверных действий или неквалифицированное выполнение технологических операций предопределяет высокие требования к уровню подготовки специалистов, входящих в состав РПП. В связи с этим возникает задача научного обоснования структуры таких расчетов и обязанностей их персонала. Для этого необходимо охарактеризовать те свойства личного состава, которые непосредственно влияют на результаты процесса подготовки, в частности, последовательность использования специалистов при выполнении работ по подготовке РКН к пуску.

Исходные данные, необходимые для решения задачи

Способ формирования РПП, состоящего из специалистов требуемых специальностей, будем характеризовать отношениями [5]:

,

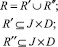где R′ – отношение, характеризующее принадлежность номеров РПП основным специальностям; R″– отношение, характеризующее возможность обучения номеров РПП смежным специальностям; D = {di}, i = 1(1)s – множество специальностей, необходимых для выполнения комплекса работ L; J = {ji}, i = 1(1)u – множество номеров РПП, u = card J – количество личного состава в РПП

Будем считать заданными также отношения:

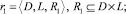
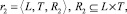
где T = {Δti}, i = 1(1)v2 – множество дискретных промежутков времени, Δti ∈ (0, τn];

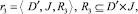
где 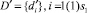– множество специальностей, по которым осуществляется подготовка номеров РПП;

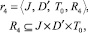
где 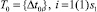– множество дискретных промежутков времени, необходимых для подготовки соответствующих специалистов;

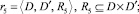
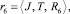
где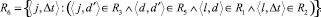

Стохастическое описание результатов ПП от свойств РПП

Результаты ПП во многом зависят от того, каким образом сформирован РПП и обеспечена ли каждая работа требуемым специалистом. Под работой понимается совокупность действий, требующая для своего выполнения только одного специалиста какой-либо специальности.

Для того чтобы охарактеризовать зависимость результатов ПП от свойств РПП, рассмотрим сложное событие, заключающееся в обеспечении выполнения всех работ l ∈ L необходимыми специалистами

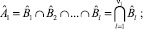
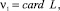(1)

где 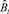– событие, заключающееся в обеспечении отдельной работы l ∈ L необходимым специалистом, card L – мощность множества L.

Рассмотрим подмножество Jl ⊂ J, в которое входят номера РПП, способные удовлетворить потребность работы l ∈ L в специалисте:

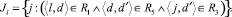(2)

Отметим, что подмножество Jl представляет собой фактор–множество (правое сечение SП по графику R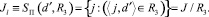3):

(3)

Обозначим через 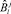событие, заключающееся в обеспечении работы l специалистом j ∈ Jl. Тогда

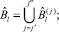
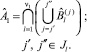(4)

Если j′ = j″, то существует единственный j-й член РПП, способный удовлетворить потребность отдельной работы или группы работ l ∈ L в специалисте. В этом случае

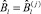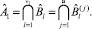и (5)

В основу формирования РПП могут быть положены различные стратегии, связанные с полной или частичной взаимозаменяемостью его номеров, или с отсутствием взаимозаменяемости. Для описания степени взаимозаменяемости номеров РПП введем отношение r7:

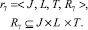(6)

Если боевой расчет формируется таким образом, что каждый номер РПП может выполнить одну или несколько работ и при этом ни один из других номеров РПП не может выполнить эти работы, то можно говорить о том, что в РПП полностью отсутствует взаимозаменяемость его членов (номеров).

Пусть 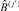– событие, заключающееся в обеспечении отдельной работы или совокупности работ l ∈ L специалистом j. Если взаимозаменяемость специалистов отсутствует и каждый специалист РПП является единственным, кто может выполнить какую-либо работу, т.е. выполняется условие:

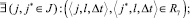(7)

то

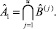(8)

Из соотношения (8) при условии, что

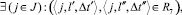
вытекает справедливость формул:

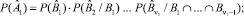(9)

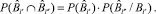(10)

Выражение (10) показывает, что в РПП предусмотрена возможность взаимозаменяемости номеров для выполнения работ в непересекающиеся промежутки времени. Таким образом, 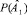является показателем возможностей РПП обеспечивать ПП специалистами.

Если в РПП не предусмотрена взаимозаменяемость специалистов, то

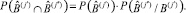(11)

Выше было отмечено, что специалист РПП может отсутствовать на рабочем месте в некоторые промежутки времени. Отсутствие членов РПП j ∈ J на своих рабочих местах в дискретные промежутки времени Δt ∈ T возникновения потребности в них носит случайный характер (болезнь, травма, вызов по служебной необходимости, неплановые отпуск, командировка и т.д.). Это можно выразить через отношение

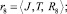
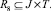(12)

Отметим, что

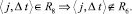(13)

Таким образом, невозможность обеспечения работы l специалистом j можно описать следующим образом. Обозначим V – невозможное событие, U – достоверное событие. Тогда, если

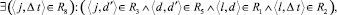(14)

то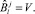

Невозможность обеспечения процесса подготовки специалистами формально описывается так: 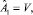если

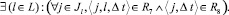(15)

Введем в рассмотрение подмножество 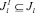, в состав которого входят номера РПП, которые имеют возможность выполнить работу l в дискретный промежуток времени Δt (т.е. не заняты в выполнении других работ и находятся на рабочих местах). Если при проведении работ ПП возможна такая ситуация, что номер расчета j, имеющий соответствующую специальность, должен одновременно выполнять две работы l′ и l″, причем он является единственным в составе расчета, способным выполнить эти работы, то он не может одновременно принадлежать к подмножествам 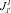и 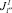. Иными словами, эти подмножества не пересекаются. Формально это записывается следующим образом. Если

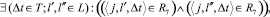(16)

то

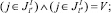
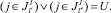(17)

В противном случае, т.е. если в любой момент времени номер расчета j может быть задействован для выполнения только одной работы, то он может принадлежать и к подмножеству 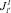, и к подмножеству 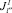. Формально это записывается так. Если

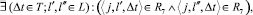(18)

то

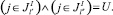(19)

В этом случае РПП можно формировать из специалистов, которые могут выполнять два и более видов работ, т.е. возможна взаимозаменяемость специалистов. Если для любого номера РПП определенной специальности, который способен выполнить работы l′ и l″, не возникает ситуация, при которой он должен эти работы выполнять одновременно (в один и тот же промежуток времени), что невозможно по условиям задачи, то он может входить в оба подмножества 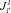и . 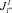Формально это записывается следующим образом:

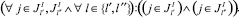(20)

Иными словами, можно агрегировать работы процесса подготовки с точки зрения обеспечения их требуемыми специалистами, то есть вместо двух работ рассматривать только одну:

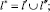
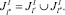(21)

Таким образом, для того, чтобы обеспечить работу l требуемым специалистом с учетом возможности агрегирования работ и взаимозаменяемости специалистов, необходимо, чтобы подмножество специалистов 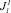обладало следующим свойством. Количество специалистов, способных выполнить работу l (это мощность подмножества 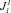), должно быть равным или превышать то количество специалистов, которое в промежуток времени Δt, определенный для выполнения работы l, задействовано для выполнения других работ ПП. В этом случае можно говорить об обеспеченности работы l требуемым специалистом. Формально это выглядит так:

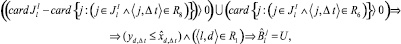(22)

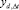где и 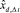количество требуемых и располагаемых специалистов d-й специальности на интервале Δt соответственно.

Дизъюнкция выражений (22) по всем работам ПП дает возможность описать событие 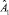, заключающееся в обеспечении всех работ ПП необходимыми специалистами.

С учетом сказанного соотношение (4) можно представить в виде:

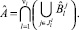(23)

Влияние расхода ресурса времени на обучение специалистов РПП учитывается через отношения r4, r3, r5, r1, так как

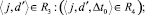(24)

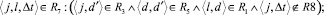(25)

Таким образом, вероятность наступления события 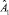выражается следующим образом:

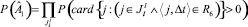(26)

или

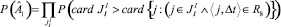. (27)

В этом выражении не учитывается воздействие неблагоприятных факторов на каждый номер РПП (возможность заболевания, получения травмы, привлечение для выполнения других работ в связи с экстренными или иными обстоятельствами и т.д.). Тогда

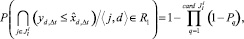(28)

где Pq – вероятность сохранения возможности для q-го номера РПП выполнить свою работу.

С учетом соотношений (1)–(6), (27) и введенных ранее понятий

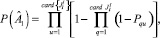(29)

где 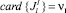– количество работ ПП.

С учетом соотношений (11), (29) вероятность обеспечения ПП специалистами РПП можно записать следующим образом:

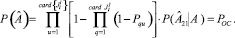(30)

Анализ выражения (30) позволяет определить основные пути повышения показателя эффективности ПП за счет совершенствования свойств РПП:

– агрегирование работ ПП путем обеспечения возможности выполнения различных работ одним специалистом, т.е. снижение величины ;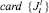

– овладение номерами РПП смежными специальностями, т.е. увеличение величины ;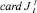

– улучшение условий выполнения ПП и организации его проведения, т.е. увеличение значения величины Pqu.

Второй путь приоритетен так как при его реализации создается резерв специалистов.

Графовая модель боевого расчета

Для разработки процедуры определения минимального количества личного состава РПП и резерва специалистов представим модель РПП в виде смешанного мультиграфа G (рис. 1), где вершины графа ji ∈ {ji} идентифицируют соответствующих членов РПП. Граф G имеет ребра трех видов. В соответствии с видами ребер существуют три части (суграфы) графа G: G1 (рис. 2), G2 (рис. 3), G3 (рис. 4).

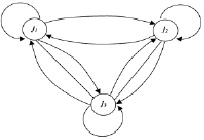
Рис. 1. Граф, характеризующийструктуру РПП

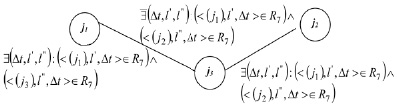
Рис. 2. Суграф G1, характеризующий возможность взаимозаменяемости номеров РПП

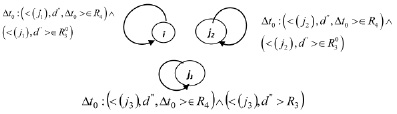
Рис. 3. Суграф G2, характеризующий временные затраты на обучение номеров РПП основным специальностям

В графе G2 каждое ребро является петлей с весом, характеризующим затраты на обучение идентифицируемого номера РПП первичной специальности.

В графе G3 вершины ji, ji+k соединены ориентированным ребром (дугой) с весом Δt0, характеризующим затраты на обучение члена РПП, имеющего первичную специальность (ji), специальности (ji+k).

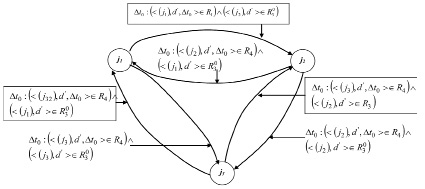
Рис. 4. Суграф G3, характеризующий временные затраты на освоение номерами РПП смежных специальностей

Заключение

Полученные результаты позволяют сформулировать задачу распределения личного состава боевого расчета по смежным специальностям и обосновать метод ее решения.

Дано:

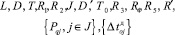
Найти:

.

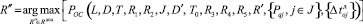Сформулированная задача относится к классу комбинаторных задач. Для её решения целесообразно использовать метод ветвей и границ [1].

Рецензенты:

Петров Г.Д., д.т.н., профессор, начальник кафедры, ВКА имени А.Ф. Можайского, г. Санкт-Петербург;

Арсеньев В.Н., д.т.н., . профессор кафедры, ВКА имени А.Ф. Можайского, г. Санкт-Петербург.

Работа поступила в редакцию 07.05.2013.

Библиографическая ссылка