Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Пивоваров А.О. 1

---

1 ФГБОУ ВПО «Волгоградский государственный технический университет»

Исследование динамики планетарных механизмов трактора показали, что основной причиной преждевременного выхода из строя является неравномерное распределение нагрузки между сателлитами, вызванное погрешностями изготовления и сборки. При этом чувствительность к этим погрешностям обусловлена наличием избыточных связей. На статически определимый механизм изменение размеров звеньев не влияет. Следовательно, статически определимые механизмы дают не только снижение трудоемкости, но и одновременно повышают долговечность. В данной работе была рассмотрена конструкция планетарной передачи без избыточных связей, что подтверждает выполненный структурный анализ и расчет по формулам Малышева и Озола. Использование данной статически определимой конструкции позволяет увеличить долговечность механизма поворота в 2 раза за счет равномерного распределения нагрузки между сателлитами и дает возможность работать механизму поворота трактора в более нагруженных условиях. Полученная конструкция и результаты исследования могут быть полезны разработчикам автотракторной техники при проектировании трансмиссий с планетарными механизмами поворота.

Статья в формате PDF

678 KB

планетарная передача

избыточные связи

гусеничный трактор

долговечность

механизм поворота

1. П м. 108526 РФ, МПК F 16 H 1/48. Планетарная передача / Вл.П. Шевчук, А.О. Пивоваров, А.В. Петренко, В.В. Шеховцов, М.В. Ляшенко, А.В. Калмыков. – Волоград: ВолгГТУ. – 2011.

2. Пивоваров А.О. Повышение долговечности планетарного механизма поворота: монография / А.О. Пивоваров, Вл.П. Шевчук. – Saarbrucken (Germany) : LAP LAMBERT Academic Publishing GmbH & Co. KG, 2012. – 105 с.

3. Пивоваров А.О. Исследование применяемых планетарных передач и механизмов на избыточные связи /А.О. Пивоваров, Вл.П. Шевчук // Вестник Академии военных наук. – 2011. – № 2 (спецвыпуск). – C. 316–321.

4. Редькин И.В. Классификация оптимальных по избыточным связям планетарных передач типа 2КН / И.В. Редькин, Вл.П. Шевчук, А.О. Пивоваров // Успехи современного естествознания. – 2012. – № 6. – C. 79–80.

5. Шевчук Вл.П. Планетарный механизм поворота с составным водилом / Вл.П. Шевчук, А.О. Пивоваров // Политранспортные системы: матер. VII всерос. науч.-техн. конф., г. Красноярск, 25–27 нояб. 2010 г. / Сибирский федеральный ун-т, Сибирский гос. ун-т путей сообщения. – Красноярск, 2010. – C. 113.

В современной автотракторной технике широкое распространение получили планетарные передачи. К достоинствам планетарных передач можно отнести большие передаточные отношения, компактность и малую массу, высокий коэффициент использования нагрузки на единицу массы. В то же время в классическом исполнении планетарные передачи относятся к многократно статически неопределимым системам, поэтому реализация их преимуществ возможна только при условии компенсации погрешностей изготовления. Они требуют повышенной точности изготовления и сложнее в сборке, что приводит к удорожанию производства.

Исследования динамики планетарных механизмов тракторов показали, что основной причиной преждевременного выхода из строя является неравномерное распределение нагрузки между сателлитами и по длине зубчатых зацеплений шестерен, вызванное погрешностями изготовления и сборки. При этом чувствительность к этим погрешностям обусловлена наличием избыточных связей или статической неопределимостью этих механизмов [3].

Избыточными (пассивными) связями называются такие связи, устранение которых не увеличивает подвижности механизма.

Целью работы является создание конструкции планетарной передачи без избыточных связей, позволяющей увеличивать долговечность механизма поворота тракторов за счет равномерного распределения нагрузки между сателлитами и по длине их зубьев. Структурный анализ данной конструкции и выявление избыточных связей при 3, 4, 5 – сателлитном исполнении.

Материалы и методы исследования

Проверить механизм на наличие в нем избыточных связей можно путем подсчета их по структурным формулам. Формула предложена Малышевым А.П. [2]:

или в развернутом виде:

где q – число избыточных связей; n – число подвижных звеньев; w – подвижность механизма; pi – число кинематических пар i-го класса, накладывает ipi условий связи. Другую структурную формулу предложил О.Г. Озол. Он поддерживает целесообразность устранения избыточных связей и дает сразу формулу для определения их числа, т.е:

где k — число независимых контуров в механизме, отличающихся от других контуров по крайней мере одним звеном или одной кинематической парой; f – сумма подвижностей кинематических пар.

Рассмотрим некоторые кинематические пары (рис. 1). Классы обозначены римскими цифрами I, II, III′, III″, IV и V, столбцы – арабскими цифрами 1–5.

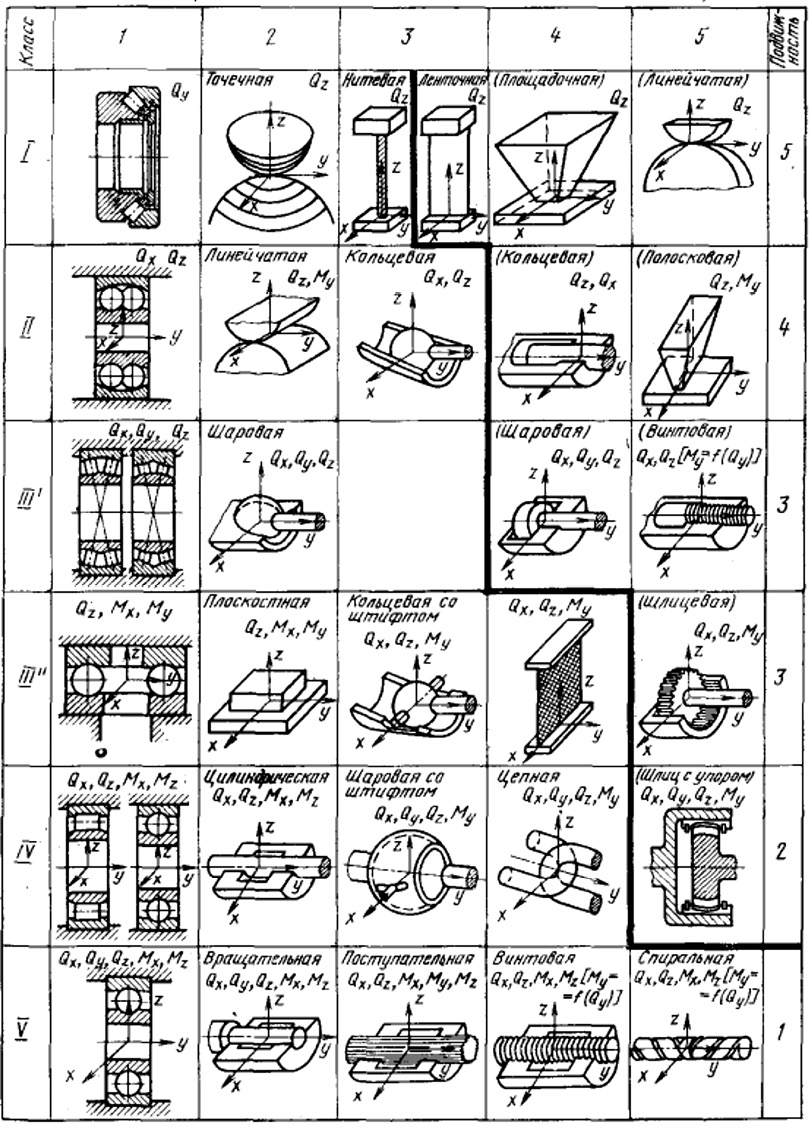
Рис. 1. Классы кинематических пар

Для каждой пары даны силы и моменты, передаваемые ею. По этой таблице можно найти подвижность кинематической пары, т.е. число движений линейных и угловых, которые она оставляет между звеньями. Вообще сумма класса пары и подвижности всегда равна шести. Для получения пары любого класса пары следует соединять параллельно. При этом сумма классов соединяемых пар равна классу получаемой пары, а при наличии избыточных связей эта сумма равна классу получаемой пары плюс число избыточных связей.

Результаты исследования и их обсуждение

Для решения проблемы статически неопределимых систем на кафедре «Автомобиле- и тракторостроение» Волгоградского государственного технического университета была спроектирована конструкция планетарной передачи [1], которая не требует повышенной точности изготовления и сборки и позволяет равномерно распределять загрузку в планетарных механизмах поворота гусеничных машин.

Указанный технический результат достигается тем, что в планетарной передаче (рис. 2), содержащей центральные колеса с внешним и внутренним зацеплением, сателлиты и водило (рис. 3), состоящее из секторов сателлитного блока и ступицы.

Причем каждый сектор представляет часть дуги окружности, секторы соединены последовательно. В средней части каждого сектора расположен сателлитный блок, состоящий из сателлита, оси и подшипника, при этом в промежутках между сателлитами расположены участки узкого шлицевого соединения, имеющие боковые и радиальные зазоры. При этом внутренние шлицы расположены на секторах сателлитного блока (рис. 4), а внешние шлицы расположены на внешних поверхностях секторов венца ступицы, секторы сателлитного блока соединены между собой карданными шарнирами для самоустановки сателлитного блока между центральными колёсами и выравнивания нагрузки между сателлитами и по длине их зубьев, с обеих сторон секторов сателлитного блока выполнены двузубые вилки. При этом с одной стороны внутренние шлицы расположены в зоне двузубых вилок, параллельных плоскости секторов сателлитного блока, а с другой стороны двузубые вилки расположены перпендикулярно плоскости секторов.

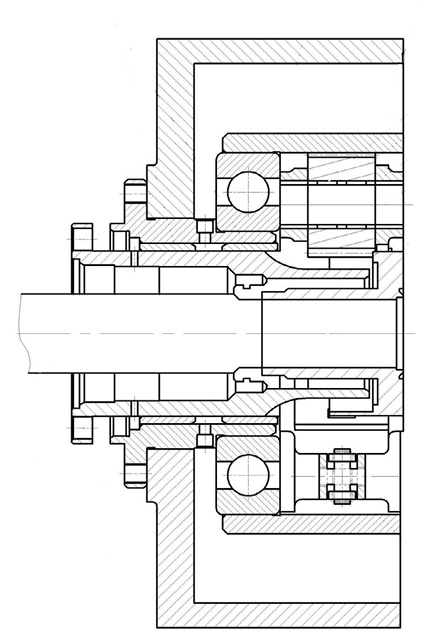
Рис. 2. Общий вид планетарной передачи в разрезе

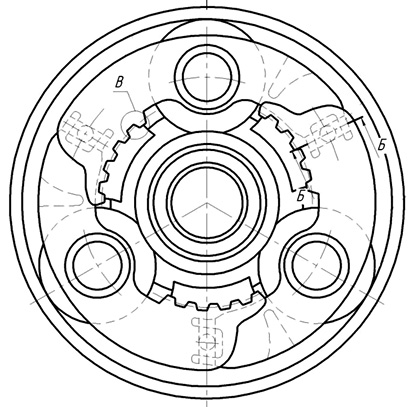
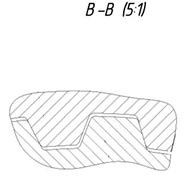
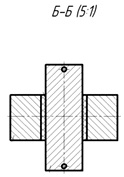
Рис. 3. Водило

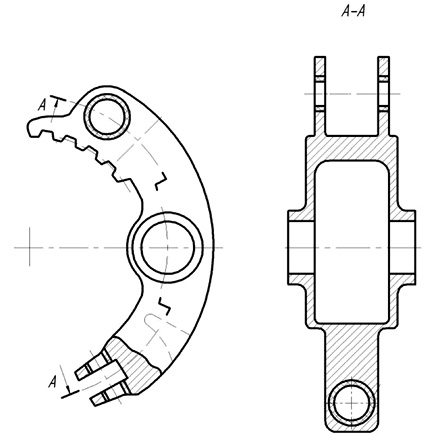
Рис. 4. Сектор сателлитного блока

Участки узкого шлицевого соединения ступицы и сателлитного блока, составленного из секторов, имеют осевые и радиальные зазоры, которые в совокупности с возможностями относительных поворотов секторов сателлитного блока за счет карданных шарниров позволяют сателлитному блоку самоустанавливаться между центральными колёсами, выравнивая нагрузку между сателлитами и по длине их зубьев.

Планетарная передача работает следующим образом.

Крутящий момент, подводимый к центральному колесу внутреннего зацепления, передается сателлитному блоку, составленному из секторов, и валу через зацепления сателлитов с центральными колесами внешнего зацепления и внутреннего зацепления. От сателлитного блока, составленного из секторов, момент передаётся ступице водила посредством участков шлицевого соединения, расположенных в промежутках между сателлитами, имеющими осевые и радиальные зазоры. Внутренние шлицы расположены на двузубых вилках, параллельных плоскости секторов сателлитного блока, а внешние шлицы – на внешних поверхностях секторов венца ступицы.

Описанная конструкция планетарной передачи позволяет повысить долговечность механизма поворота тракторов за счет того, что сателлитный блок, состоящий из секторов, соединенных посредством карданных шарниров, а ступица с сателлитным блоком соединены узким шлицевым соединением, которое в совокупности с карданными шарнирами позволяет одновременно выравнивать нагрузку между сателлитами и по длине зубчатых зацеплений сателлитов с центральными колесами.

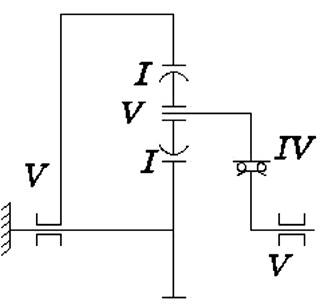
Рис. 5. Структурная схема

Таблица 1

Результаты расчета по формуле Малышева А.П.

Таблица 2

Результаты расчета по формуле Озола О.Г.

Из результатов расчета следует, что планетарная передача не имеет избыточных связей при 3, 4, 5 сателлитах. Это позволяет говорить о том, что данный механизм статически определимый.

Заключение

Итогом работы является создание новой конструкции планетарной передачи без избыточных связей, т.е. статически определимым, что подтверждает выполненный структурный анализ и расчет по формулам Малышева и Озола. Данная конструкция должна не только равносильно заменять существующие, но и увеличивать ресурс работы механизмов поворота гусеничных тракторов в 2 раза, что равняется 12–15 тыс. моточасов, а так же давать возможность работать механизмом в более нагруженных условиях.

Рецензенты:

Ляшенко М.В., д.т.н., профессор, заведующий кафедрой АТС, Волгоградский государственный технический университет, г. Волгоград;

Шеховцов В.В., д.т.н., профессор, Волгоградский государственный технический университет, г. Волгоград.

Работа поступила в редакцию 10.04.2013.

Библиографическая ссылка