Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Волынов М.А. 1

---

1 ГНУ «Всероссийский научно-исследовательский институт гидротехники и мелиорации им. А.Н. Костякова»

В статье рассмотрено влияние плановой геометрии речного русла на процесс рассеяния примесей. Перенос примесей из одних частей речного потока в другие его части осуществляется кроме механизма турбулентной диффузии также и механизмом конвективной дисперсии. С использованием гипотезы Буссинеска и динамического уравнения для потока на повороте русла показано, что подобие течения в этом случае определяется не только числом Фруда, но также произведением степени распластанности русла на коэффициент гидравлического сопротивления. На основе обобщения лабораторных и натурных данных получены формулы для коэффициентов эффективной диффузии примесей в продольном и поперечном направлении по отношению к оси потока. Для течения на повороте русла получено условие равенства продольной и поперечной составляющих напряжения трения. Предложено выражение для коэффициента поперечной эффективной диффузии на повороте речного потока, отражающее влияние распластанности русла, радиуса поворота и коэффициента гидравлического сопротивления. Установлена степень влияния турбулентной составляющей на процесс переноса примесей. Показано, что масштаб турбулентных образований, ответственных за рассеяние примеси в распластанных руслах, соизмерим с глубиной потока. Полученные зависимости для эффективных коэффициентов продольной и поперечной диффузии позволяют производить расчеты рассеяния примесей на прямолинейных участках русел и в излучинах с использованием одномерных и двумерных идеализаций течения.

Статья в формате PDF

1108 KB

речной поток

турбулентная диффузия

конвективная дисперсия

коэффициент эффективной диффузии на прямолинейных участках и поворотах речного русла

1. Каплин В.Т. Превращение органических соединений в водоемах // Гидрохим. материалы. – 1967. – т. 45. – С. 207–226.

2. Монин А.С., Яглом А.М. Статистическая гидромеханика // Механика турбулентности. Ч. 1. – М.: Наука, 1965. – 639 с.

3. Шеренков И.А. Прикладные плановые задачи гидравлики спокойных потоков. – М.: Энергия, 1978. – 240 с.

4. Elder J.W. The dispersion of marked fluid in turbulent shear flow // J. Fluid Mech. – 1959. – № 4. – Р. 544–560.

5. Лятхер В.М., Прудовский А.М. Гидравлическое моделирование. – М.: Энергоатомиздат, 1984. – 390 с.

6. Пааль Л.Л., Тутт М.А. О расчетах концентрации вещества загрязнения в реках при периодических выпусках сточных вод // Доклад и сообщ. по вопросам самоочищения водоемов и смешения сточных вод. – Таллин, 1967. – С. 38–45.

7. Bansal М.К. Dispersion in natural streams // J. Hudr. Div. Proc. ASCE. – 1971. – Р. 1866–1867.

8. Fesher H.P. Longitudinal dispersion and turbulent mixing in open channel flow // Ann Rev. Fluid Mech. – 1973. – № 5. – Р. 59–78.

9. Курдюмов Л.Д. Закономерности эрозионно-аккумулятивного процесса. – Л.: Гидрометеоиздат, 1977. – 134 c.

10. Beltaos S. Transverse mixing in natural streams // Can. Journ. Civ. Eng. – 1979. – Vol. 6. – Р. 4.

Различные примеси, поступающие в речную сеть, имеют значительные периоды распада [1], что позволяет рассматривать их во многих задачах переноса как консервативные. Характерной особенностью речных потоков является их распластанность при ширине, многократно превышающей глубину. Это приводит к сравнительно быстрому выравниванию концентрации по глубине потока, что позволяет рассматривать процесс переноса как двумерный и производить расчет в рамках плановой задачи. Уравнения переноса в этом случае имеют вид [2]:

(1)

где С – средняя по глубине концентрация примеси; Сn, Cs – концентрация примеси соответственно у поверхности и вблизи дна; h = Hср – z0; w – гидравлическая крупность взвеси; s, n, z – криволинейные координаты соответственно продольная, поперечная и вертикальная; – поток примеси через свободную поверхность и дно соответственно; e – коэффициент турбулентной диффузии.

Два указанных механизма рассеяния примесей действуют одновременно и, как обычно считается, независимо один от другого. Эта независимость является в достаточной степени условной, поскольку неравномерность распределения скоростей по поперечному сечению потока тесно связана с его турбулентной структурой. Трудность анализа процесса переноса в трехмерной и даже в двухмерной постановке часто заставляют принимать одномерную модель явления и с использованием гипотезы Буссинеска суммировать эффект этих двух механизмов с помощью так называемого суммарного или эффективного коэффициента диффузии [3]

De = Dк + Dт1, (2)

где Dк – слагаемое, связанное с конвективной дисперсной; Dт1 – коэффициент турбулентной диффузии.

Процесс конвективного переноса примеси в широком канале был рассчитан Дж. Элдером [4], причем установлено, что составляющая Dк коэффициента эффективной диффузии при этом значительно превосходит Dт1. По результатам исследований Дж. Эйлера было установлено, что D = 6,1u*h. Однако экспериментальные исследования показали, что числовой множитель в этом соотношении не остается постоянным, а изменяется в широких пределах от 6 до 25 и более. На величину этого коэффициента оказывает влияние не только вертикальный профиль скорости, но также плановое распределение скорости и интенсивность возникающих вторичных течений. Возможно, именно неустойчивость вторичных течений рождает наиболее крупномасштабные нерегулярности течения в потоке. В тех случаях, когда относительная ширина потока становится небольшой, система вторичных течений изменяется в зависимости от , что сказывается существенно на процессах переноса. Отмечается также [5], что и коэффициент гидравлического сопротивления, характеризующий процесс переноса импульса, начинает зависеть от относительной ширины потока при . Влияние относительной ширины потока особенно сильно проявляется в условиях большой шероховатости, заметной неоднородности дна и боковых частей русла, а также при наличии поворотов потока. Наличие поворотов, неодинаковость шероховатости по смоченному периметру, влияние боковых поверхностей трения приводит к образованию интенсивных циркуляций в потоке, связанных с искривлением траекторий движущихся жидких частиц с отклонением их от направления осредненного течения.

Рассмотрим динамическое равновесие элемента потока, движущегося на повороте русла стационарно с радиусом кривизны r. Уравнение равновесия в проекции на ось x2, совпадающую с радиусом кривизны, имеет вид

(3)

где v – радиальная компонента скорости течения; – поперечный уклон свободной поверхности потока; – поперечная компонента сил трения.

При этой записи уравнения баланса сил геометрия сечения в поперечном направлении считается не изменяющейся. Учитывая пропорциональность между и , и заменяя производную по х2 ее оценкой, преобразуем уравнение баланса к виду

(4)

Считая, что радиус кривизны соизмерим с шириной потока r ~ B имеем

(5)

Отсюда уравнение баланса сил находим в критериальном виде

(6)

Таким образом, при наличии интенсивных поперечных циркуляций (вторичных течений) подобие сил определяется не только числом Фруда, но также и дополнительным критерием , что согласуется с позицией В.М. Ляхтера и А.М. Прудовского по данному вопросу [5].

При анализе данных по коэффициенту эффективной диффузии обычно сопоставляют безразмерный комплекс с величиной . С учетом полученных выше результатов был выполнен анализ лабораторных и натурных данных по величине продольного коэффициента эффективной диффузии. Использованы данные Таллиннского политехнического института [6, Пааль] и данные других авторов. Результаты обобщения данных в координатах представлены на рис. 1.

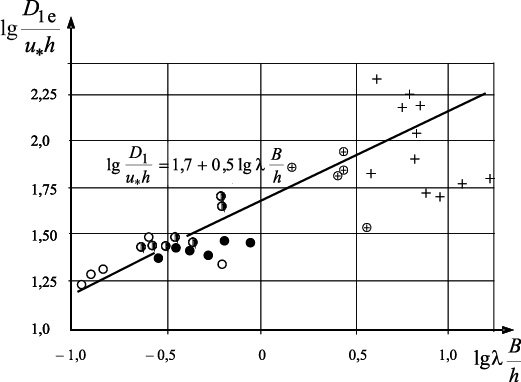
Рис. 1. Данные Таллинского политехнического института [6]: (лабораторные данные)
— шероховатость малая;
— шероховатость средняя;    
— шероховатость большая;
⊗ — незаросшие чистые русла;
+ — русла, заросшие на 10 % и менее

Данные по естественным водотокам отобраны лишь те, которые относятся к чистым и слабозаросшим руслам. Результаты лабораторных и натурных исследований (см. рис. 1) удовлетворительно аппроксимируются зависимостью

(7)

которая может быть записана и в иной форме:

(8)

Зависимость получена по опытным данным в диапазоне изменения . Можно предполагать, что при увеличении степень зависимости от будет ослабевать, однако надежных количественных данных, подтверждающих это предположение, пока не имеется.

Перенос примеси в поперечном направлении также характеризуется эффективным коэффициентом поперечной диффузии D2e, который равен сумме коэффициентов поперечной дисперсии и поперечной турбулентной диффузии. Как показывают расчеты и экспериментальные исследования, интенсивность поперечного переноса значительно более низкая по сравнению с переносом в продольном направлении. По данным исследования М. Бансала [7], обобщившего обширные натурные данные, эффективный коэффициент поперечной диффузии определяется относительной шириной русла (рис. 2).

Данные могут быть аппроксимированы следующей зависимостью:

(9)

Следует отметить также, что зависимость от при весьма больших значениях (вплоть до ) представляется труднообъяснимой.

Ряд исследователей указывает на существенное влияние извилистости русла [8]. При извилистом русле массы жидкости на повороте находятся под действием центробежных сил, направленных по радиусу кривизны r

(10)

где m = ρh∙1∙1 – рассматриваемая масса жидкости.

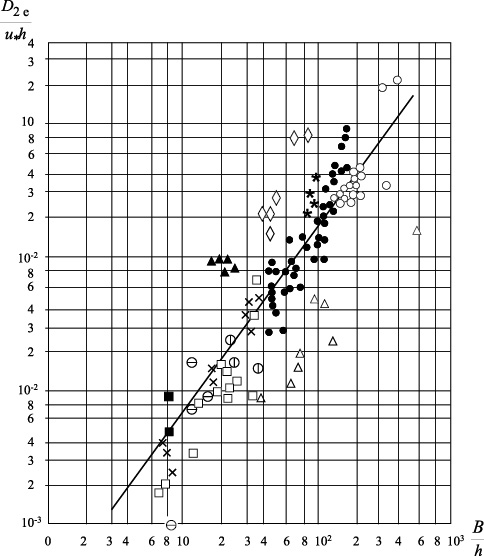
Рис. 2. ◊— р. Миссисипи; — р. Канзас; △— р. Смуки Хилл; y— р. Салина; — р. Соломон; □ — р. Биг Блю; ● — р. Миссури; ╳— р. Патуксент; ■ — р. Патомак; ▲ — р. Грин; * — р. Саут Платт

Одновременно масса жидкости участвует в продольном движении и находится под действием продольных касательных напряжений τ0. Сопоставим величину напряжений, возникающих от действия центробежных сил с продольными касательными напряжениями. Найдем напряжения от действия центробежных сил в виде

(11)

где – продольная динамическая скорость.

Тогда

(12)

Эти напряжения равны по величине, если

(13)

При среднем значении – это соотношение определяет кривизну потока, при которой продольные касательные напряжения и центробежные напряжения равны. При центробежные напряжения превышают продольные касательные напряжения. Можно предположить, что поперечные составляющие пульсации скорости в этих случаях будут связаны с неустойчивостью криволинейного движения и будут определяться величиной центробежных напряжений:

(14)

Поскольку вторичные течения захватывают всю ширину потока, очевидно, что масштаб турбулентности, определяющий эффективный массоперенос в этом случае, будет пропорционален ширине потока В. Тогда эффективный коэффициент диффузии оказывается связанным с интегральными параметрами потока следующим соотношением:

(15)

где – отношение поперечного масштаба к ширине русла.

Таким образом, находим, что

(16)

Как известно, радиус кривизны потока r для естественных водотоков может задаваться произвольно лишь в условиях лаборатории. В условиях естественного водотока r ~ K2B, причем для равнинных условий величина K2 = 5...10 [9]. Следует отметить, что величина масштаба L2e пропорциональна ширине потока, по-видимому, лишь при B/h < 20...30. При большей относительной ширине потока связь между масштабом возмущений и шириной потока должна теряться. (Известно, что при В/h > 20 процесс переноса импульса перестает зависеть от B/h). Поэтому в дальнейшем при обработке экспериментальных данных величина K1 принималась равной 1 при B/h < 30. Если величина r не была известна, то она принималась по соотношению r = K2B при K2 = 7,5В. Результаты обработки экспериментальных данных ряда авторов [10] в координатах представлены на рис. 3.

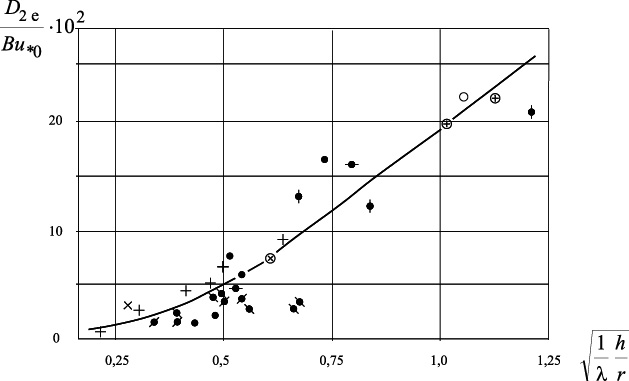
Рис. 3. + — данные Беатлоса (р. Атабаска); ⊕— данные Энгманна (р. Лессерслейс); ○— данные Сэйра (р. Миссури); ╳ — данные Йоцукури (р. Миссури); ⊗ — данные Гловера (р. Колумбия). Лабораторные криволинейные каналы: ●— данные Фишера; — данные Энгманна; — данные Энгманна (ледовый режим); — данные Кришнапанна

Поскольку для имевшихся натурных данных не были известны значения r, при их обработке учитывалось, что

С достаточной для натурных измерений точностью данные, приведенные на рис. 3, могут быть аппроксимированы соотношением:

(17)

которое справедливо для .

Выполненная обработка натурных данных с последующим сравнением результатов с данными лабораторных измерений позволили установить их отчетливую качественную схожесть. Количественное совпадение достигалось подбором К1 при среднем значении К2 = 7,5. Общая сводка результатов обработки, представленная на рис. 3, позволяет отметить хорошее согласие результатов лабораторных и натурных измерений, в том числе и для потоков с относительной шириной В/h > 25...30 при выборе К1 = 0,01. Это указывает на то, что в условиях очень широкого русла масштабы возмущений, ответственных за перенос веществ в поперечном направлении, составляют (1...2)∙h. Приведенная выше аппроксимационная зависимость показывает, что при центробежные напряжения становятся близкими к продольным касательным напряжениям и интенсивность возмущений и их масштаб определяются в основном параметрами продольного течения. В этих условиях поперечный перенос будет носить практически чисто диффузионный характер. Согласно имеющимся данным [10], коэффициент поперечной турбулентной диффузии в этом случае , что отвечает

При значение коэффициента поперечной турбулентной диффузии согласуется с данными, приведенными на рис. 3.

Полученные зависимости для эффективных коэффициентов продольной и поперечной диффузии позволяют осуществлять расчеты переноса примесей в речных потоках с использованием одномерных и двумерных идеализаций явления.

Рецензенты:

Боровков В.С., д.т.н., профессор кафедры гидравлики Московского государственного строительного университета, г. Москва;

Скворцов Л.С., д.т.н., генеральный директор ООО «Экотех-Москва», г. Москва.

Работа поступила в редакцию 16.04.2013.

Библиографическая ссылка