Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Бейсембаев К.М. 1 Шманов М.Н. 1 Жетесов С.С. 1 Мендикенов К.К. 1 Абдугалиева Г.Б. 1

---

1 Карагандинский государственный технический университет

Анализ известных внезапных разрушений сооружений и систем показывает, что причины аварий не однозначны. Разработаны требования и программа, моделирующая движение системы и позволяющая дать трактовку возможности внезапного изменения формы системы при накоплении критического значения повреждений (формообразований), когда происходит скачкообразный рост напряжений в их элементах, инициирующих автоколебания и аварии. Для геомеханической системы недр с движущимися выработками описаны факторы основных проявлений горного давления, обеспечивающих фиксацию формоизменений системы, которые связаны с особенностями расположения и раскрытия трещин в породах и пластах, опусканиями и подъёмами отдельных участков почвы выработок на карагандинских шахтах. Внезапное изменение формы системы способно инициировать и газодинамические явления в виде массовых обрушений пород, внезапных выбросов угля и газа. Результаты работы могут применятся при разработке систем управления лавами.

Статья в формате PDF

550 KB

формоизменение

колебание

программа

внезапные выбросы

1. Александров А.В., Потапов В.Д., Зылев В.Б. // Строительная механика. Книга 2. Динамика и устойчивость упругих систем. – 384 с.

2. Мельников Н.Н., Калашник А.И., Калашник Н.А. Техногенные геодинамические процессы при освоении нефтегазовых месторождений шельфа Баренцева моря // Вестник МГТУ. – 2009. – Т. 12. – № 4. – С. 601–608.

3. Сапожников В.Т. Предельно-напряженное состояние угольного пласта // Физико-технические проблемы разработки месторождений полезных ископаемых. – 1988. – № 3. – С. 56–60.

4. Зональная дезинтеграция горных пород вокруг подземных выработок / Е.И. Шемякин, Б.Л. Фисенко, М.В. Курленя, В.П. Опарин, В.Н. Рева, Ф.П. Глушихин, М.А. Розенбаум, З.А. Тропп, // Физико-технические проблемы разработки месторождений полезных ископаемых. – 1987. – № 1. – С. 3–8.

5. Физические и информационные аспекты формоизменения сооружений / К.М. Бейсембаев, Ю.А. Векслер, М.У. Исабеков, С. Сатаров // Вестник Карагандинского государственного университета им. Е.А. Букетова: серия физика. – Караганда, 2006. – № 2 (42). – С. 53–62.

6. К разработке новых машинотехнологических систем и их моделей / К.М. Бейсембаев, С.А. Жакенов, С.С. Жетесов, И.Н. Демищук, М.Н. Шманов, И.Д. Тир, Н.С. Малыбаев // Уголь. – 2011. – № 4. – С. 69–71.

7. Бейсембаев К.М., Жетесов С.С., Шманов М.Н. Исследование особенностей состояния горных пород в недрах // Алматы: Комплексное использование минерального сырья. – 2009. – № 3. – С. 3–11.

Современные технологии моделирования на компьютерах становятся независимыми от теоретических методов обосновывающих решения [5, 6]. Это приводит к ошибкам в результатах, особенно в прикладных исследованиях, где часто используют вычислители из приложений, например, метод конечных элементов (МКЭ). Проблемы с точностью вычислений возможны в специальных зонах, оказывающих большое влияние на состояние конструкций. Причины возникновения таких зон точно не определены, а ошибки в расчётах выявить трудно. Но они могут быть причинами внезапного разрушения сооружений, (катастрофы парка Трансвааль в России, ряд катастроф в Германии и Польше в начале 2000 годов и аварии при нефтеразработках) [2]. Их причины так и не были определены или предположены. Интересен случай в Волгограде: образование волн деформаций моста через Волгу. Причины некорректного построения расчёта из-за решателя имели место во многих сложных конструкциях, но здесь имеем факторы, принципиально не входящие в существующие регламенты и методики расчёта. По нашему мнению, они происходят из-за внезапного изменения формы всей системы. Близкие к ним расчёты на устойчивость конструкции ранее в основном относили к стержневым конструкциям или оболочкам, где указанные факторы заметны визуально. Так, по Эйлеру, изгиб стержня в форме синуса мог внезапно изменить выпуклости на впадины. Из практики известно и изменение формы тонкостенных конструкций под воздействием температуры, обычно сопровождаемое звуковыми эффектами и колебаниями [1]. Для относительно толстых конструкций визуализация затруднена, поскольку абсолютные величины деформаций невелики. Изменение формы в соответствии с физическим представлением объясняется переходом энергетического состояния системы в другое, когда прежняя уже «не выгодна». В этот момент напряжения в конструкции нелинейно возрастают и их рост вызывает изменение формы, а если конструкция тонкостенна, то и явные автоколебания системы. В работе для подтверждения новых выводов используются ссылки на ранее выполненные исследования авторов.

Фиксация факторов и уточнения решений

Реальный массив при подземной разработке угля лавой подвержен дезинтеграции его элементов, развитию системной трещиноватости и, несмотря на разделение, некоторой части слоёв расслоениями и поперечными трещинами во многих случаях может быть относительно целостным и в то же время иметь достаточные степени свободы и повышенные возможности к деформациям [3, 7]. В такой системе имеются условия для внезапного изменения формы. Фиксация этого явления на практике возможна по быстро затухающему для толстостенной конструкции акустическому излучению. Модель такой геомеханической системы сложна (включает различные породы вокруг лавы и выработок до земной поверхности, схемы обрушений с зависанием консолей и сводо­образованием пород). Для ряда сценариев проведено статическое решение в напряжениях и деформациях, которое заканчивается разного вида разрушением некоторого элемента, после чего автоматически рассчитывается новый сценарий. Обычно на начальном этапе напряжения изменяются не намного, причём для геомеханической системы вблизи лавы они для каждого последующего сценария несколько возрастают, а резкий их рост (здесь же требуется и повышенная точность расчёта) свидетельствует о начале бифуркации или, точнее, многозначности состояния системы [2, 5, 6]. Статические решения, учитывающие формоизменения элементов, не позволяют фиксировать колебания системы, но фиксируют циклические изменения системы, когда она повторяет своё состояние, вызывая зацикливание компьютерной программы. Чтобы создать такую программу, имеющую множество новых элементов, следует её предельно упростить и использовать комплексные решения. Мы рассмотрели пласт с нависающими над ним вначале двумя, а затем тремя консолями пород. Упрощенные конечные элементы вводились между консолями и пластом. Исследовав особенности поведения пласта и консоли, вводили дезинтеграцию пласта (постепенное разделение его на участки с различными физико-механическими свойствами (рис. 1)), что позволило оценить особенности нагружения пластовой зоны. Для ускорения расчёта консоли не разбивались сеткой, а описывались уравнениями теории упругости. В результате легко отслеживались формоизменения, волновой характер распределения нагрузки, особенности отслоений участков слоёв, их порядок в слоях, деформации и осадки участков пласта при дезинтеграции [4, 5]. Чтобы точнее описать изменяющуюся систему, следует рассматривать не только разрушение некоторых элементов системы (поперечное разрушение, отслоение), но и увеличение их подвижности за счёт скачкообразного изменения модуля деформации. Поэтому иногда вместо термина «разрушение» используется термин «формоизменение элементов», который не следует путать с формоизменением системы. Для точной оценки изменения состояния системы компьютерной модели недостаточно, и мы использовали простую стендовую модель из фотоупругого материала, что дало возможность отслеживать качество эксперимента. Затем пригрузку в компьютерной модели, имитирующую вышезалегающие породы, заменили полуплоскостью (имитация пород до поверхности земли) с соответствующими уравнениями взаимодействия полуплоскости и верхней консоли. Таким образом, имея относительно небольшой программный код и соответственно хорошие возможности контроля ошибок программирования и логики решения задачи, мы получили возможности сосредоточиться на программе фиксации формоизменений элементов (разрушений) различного вида, когда приходилось сравнивать виды разрушения и находить универсальную оценку для приоритетного выбора одного из них для каждого расчётного цикла [5, 6], а также программу автоматического учёта формоизменения и продолжения расчёта в новом состоянии, сбросив отчёт в файлы данных. Фиксация нелинейного роста напряжений происходит только тогда, когда система накапливает минимальный уровень формоизменения элементов и становится относительно свободной (предотвратить такие нарушения невозможно из-за необходимости огромных усилий управления) при этом попытки их предотвращения ведут к тому, что они возникают в других зонах. Затем напряжения уменьшаются, и система как бы стремится повторить прежнее состояние, хотя и на новом уровне. Расчётные данные приведены в [6]. Выявлены случаи смыкания поверхностей, где ранее были отслоения, что повторялось не раз. Так, статическое решение позволяет имитировать стремление системы к колебаниям. Заметим, что в компьютерных прикладных исследованиях не должна происходить потеря логики, задачи и формоизменения на отдельных участках разрушения должны надёжно фиксироваться и объясняться. Следует построить процессную модель явления, отражающую «здравый смысл», а неоднозначные результаты объяснять известными физическими принципами, так, зафиксированные некоторые отслоения могли объясняться волнообразным распространением напряжений, полученных вначале на упрощенной, а затем и на твёрдотельной модели, и, наконец, зафиксированных в шахтных условиях [7]. Но для фиксации явления следует проанализировать возможности получения подтверждающих факторов на основе заранее изученных схем основных проявлений горного давления (ОПГД) у выработок. Вначале следует проверить принцип волнообразного распределения давления у обнажений. Причём его проще выявить при наличии зависающих над пластом консолей пород (рис. 1) у лав, а также при наличии выработок, пересекающих пласт, при приближении к ним лавы. При балочных решениях, когда, слои пород принимаются за балку, а пласт за их упругое основание, такое распределение легко получить аналитически. Однако для плоских и объёмных решений на основе теории упругости широко известные работы отсутствуют. Нами оно было получено и при использовании МКЭ с введением зон пластовой дезинтеграции. Таким образом, «длина волны» зависит от длины участка дезинтеграции, в призабойной зоне она короче, чем за её пределами. В таблице приведены некоторые схемы ОПГД, классифицированные ранее и полученные на основе теоретического анализа с их последующей фиксацией в шахтных условиях. Эти проявления практически не встречаются в публикациях, хотя опытным горнякам хорошо известны. Это, в частности, подъемы участков пород и опускания соседних, зияющие трещины в почве и пласте (поперек и вдоль напластования), что обосновано шахтными наблюдениями. Здесь индексы 1.1.1.2, 1.1.1.2.1, 1.1.1.2.1.2 представляют поперечный разлом пласта при опускании его участка (трещина разрыва направлена сверху вниз), 1.1.1.2.3 –трещины сверху и снизу при подъёме–опускании волнообразно деформированного пласта. Индекс 4.2.1 – отрывная трещина в груди забоя вдоль напластования чаще всего при приближении лавы к выработке, пересекающей пласт (обычно под углом к лаве до 15°), или в стенках стационарных параллельных выработок, в результате подъёма части пласта. Его подъём сопровождается опусканием другой части, и происходит видимое расхождение берегов трещины – зияние. Причина этого в том, что через пласт проходит линия относительной симметрии формообразования слоев пород (рис. 1). Т.е. если породы над линией опускаются, то под ней поднимаются.

Выкопировка из схем основных проявлений горного давления (ОПГД) на ш. Кировская, им. Костенко и др.

Во многом аналогична и картина трещинообразования пород снизу и сверху, что зафиксировано в схемах ОПГД. Причём это касается не только трещин давления, кратных шагу захвата комбайна (уголь в лаве вынимается последовательными полосами шириной 0,63 м), но и поперечными к слоям трещинам, имеющим существенно больший шаг, определяемый в основном изгибом пород. Зияющая трещина может открываться и закрываться как при движении лавы, так и в стационарных выработках, но зафиксировать её в последних проще, т.к. время существования трещины намного дольше. По скоростям изменения раскрытия трещины или по скоростям опускания–подъёма почвы можно судить о природе процессов в недрах [7]. Внезапные всплески напряжений могут инициировать процессы массового обрушения пород у горных выработок (ш. Абайская, 2008 г., Караганда), а также такие явления, как внезапные выбросы угля, газа и пород. Заметим, что частично эти закономерности образования системных трещин характерны не только для геомеханики выемочных работ в недрах, но и для других систем, имеющих стесненные условия деформирования и нагрузки, превышающие пределы прочности. Представление системы в виде «склеенных» элементов (рис. 2) позволяет существенно упростить и расчётные условия образования трещин, а значит, и упростить код программы, сконцентрировав анализ логики процессов вначале на основных факторах. Такую систему можно рассматривать как сплошную (при теоретическом решении), склеенную или имеющую по граням контакт – элементы (если используется МКЭ). При этом разрушения упрощенно рассматривается по 2 направлениям – по ребрам элементов. Условия разрушения также существенно упрощаются и возможно использование критерия предельных напряжений. Кроме того, для элементов объекта можно рассмотреть и формообразования внутреннего характера типа «уплотнение–разуплотнение», которое учитывается, например, скачкообразным изменением модуля деформации (упругости) и коэффициентом Пуассона. При этом резко возрастают зазоры между ядрами структуры, в которых упаковка частиц уплотняется [7]. Легко проверить и результаты решения, сравнивая их с экспериментом. Формообразования по 1, 2 в общем случае требуют изменения исходных данных в каждом расчётном цикле и соответствующего построения автоматизированного алгоритма. Причём время обработки данных программой с ростом формообразований типа 2 будет резко возрастать. Действительно, появление 2 требует его учёта за счёт преобразования матрицы линейных коэффициентов уравнений в системе расчёта МКЭ, где вычёркиваются строки и столбцы на пересечении с номером элемента. Если в следующем цикле расчёта возникло и разрушение 3, то надо вернуться к восстановлению матрицы с элементом 2, в которой учтено и 3, поскольку трещина 2 может сомкнуться и «суметь» воспринимать нагрузки сжимающего характера, т.е. в расчёте появляется лишний цикл. При увеличении количества трещин типа 2, 3 растёт число возможных схем вариантов (комбинаторик) восстановления трещин, которые надо проверить, а значит, время расчёта резко возрастёт.

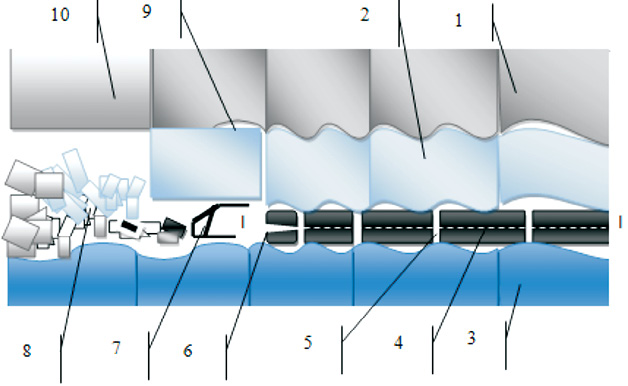
Рис. 1. Схема волнообразных деформаций в лаве: 1, 2 – породы кровли; 3 – почва; 4 – участок пласта; 5 – трещина дезинтеграции пласта; 6 – зияющая трещина; 7 – крепь; 8 – обрушенная порода; 9 – трещина отслоения; 10 – разгруженная зона пород; I–I – линия относительной симметрии

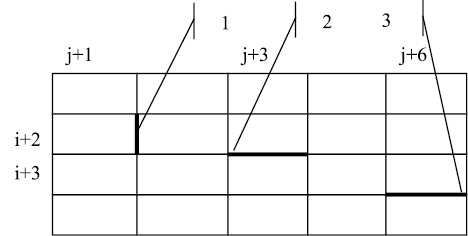
Рис. 2. Модель с системными ослаблениями, где реализуются формообразования с поперечными (1) и продольными (2) направлениями на участках оконтуренных ослаблениями

Выводы и прогнозы

Таким образом, для класса систем в которые могут входить геомеханические системы недр, сооружения и сложные конструкции, разработаны элементы позволяющие уточнить расчёт и получить модель процесса формоизменения системы в целом или на её некотором обширном участке. Внезапное изменение формы системы может прогнозироваться по расчётам программ, определяющих внезапный рост напряжений при достижении критического объёма повреждений. При этом программа расчёта должна обеспечивать учёт движения системы (подвигание работ в лаве, формоизменения закрепляющих элементов) в автоматическом режиме. В натуре этот процесс сопровождается специфическим акустическим фоном. В лаве его можно также фиксировать по проявлениям напряженного состояния массива, отражаемого в записях давления гидростоек и анализу ОПГД вокруг выработок. Не учёт этих явлений может привести к крупной аварии, внезапным газодинамическим явлениям. Заметим, что в недрах эти условия сложнее и складываются редко. Для этого система должна достичь необходимого уровня формоизменений её отдельных элементов, и в тоже время поведение системы должно сохраняться как целостной. Так, породные слои при наличии отслоений и поперечных разломов должны оставаться способными воспринимать на протяжении зоны горных работ изгибные напряжения. Это возможно в том случае, когда основная масса формоизменений в массиве имеет системный характер.

Рецензенты:

Грузин В.В., д.т.н., профессор, заведующий кафедрой «Строительные и дорожные машины», Карагандинский технический университет, г. Караганда;

Глотов Б.Н., д.т.н., профессор, директор института дистанционного и заочного обучения, Карагандинский технический университет, г. Караганда.

Работа поступила в редакцию 11.04.2013.

Библиографическая ссылка