Основы теории нечетких множеств были заложены в работе профессора университета Беркли в Калифорнии Лотфи Заде [5]. В теории множеств обычное («четкое») множество А рассматривают как часть некоторого универсального множества U. Пример: U – множество всех типов аккумуляторов, А – множество свинцово-кислотных аккумуляторов. В этом случае о каждом элементе универсального множества можно сказать однозначно, принадлежит ли он множеству А. Если ввести понятие функции принадлежности элемента четкому множеству А, то она будет принимать два значения: 1 – если элемент принадлежит множеству А и 0 – в противном случае.
Основная идея [5] заключалась в том, что для некоторых типов объектов функция принадлежности может принимать любые значения на отрезке [0; 1]. В этом случае значение функции принадлежности характеризует вероятность принадлежности элемента множеству А.
В дальнейшем в работах Л. Заде и его последователей были введены понятия операций на нечетких множествах, нечеткого логического вывода и введено понятие лингвистической переменной, в качестве значений которой выступают нечеткие множества. В инженерной практике появилось понятие «нечеткого» управления, когда управление сложным техническим объектом происходит в условиях неполной и/или недостаточно формализованной информации. Подобный подход используется как в моделировании сложных технических объектов [2], так и для создания реальных устройств автоматического управления подобными объектами.
В настоящей работе рассматривается применение методов нечеткой логики к моделированию системы управления зарядовым устройством батареи в пакете прикладных программ Mathcad.
Принципы создания модели на основе нечеткой логики
Как было отмечено выше, в основе формализма нечеткой логики лежат понятия нечетких множеств, нечетких высказываний и т.п. Методы нечеткой логики относятся к так называемым «мягким» вычислениям, основанным на вероятностном подходе. В нечеткой логике введено понятие нечеткой функции и разработана концепция построения нечетких регрессионных моделей. В рамках такого подхода было введено понятие нечеткой лингвистической переменной, значения которой могут быть выражены в терминах типа «низкая», «умеренная», «большая», «очень высокая» и т.п. Множество значений нечеткой переменной образуют так называемое терм-множество. Например, переменная «Температура» может обладать терм-множеством значений {«Очень низкая», «Низкая», «Средняя», «Высокая», «Очень высокая»}.
Основными видами функций принадлежности являются треугольные, трапециевидные, кусочно-линейные, гауссовы, сигмоидные и другие функции. Для задания трапециевидной функции принадлежности необходимы четыре параметра, определяющие х – координаты выделенных точек (рис. 1).
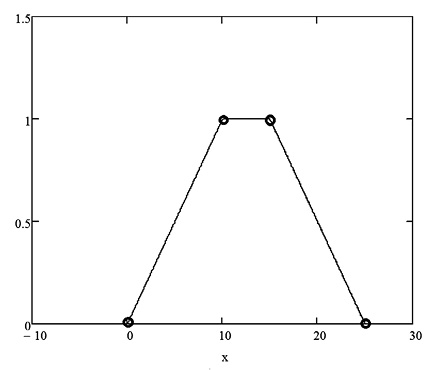
Рис. 1. Параметры трапециевидной функций принадлежности
Говоря о нечеткой логике, чаще всего имеют в виду системы нечеткого вывода, которые лежат в основе различных экспертных и управляющих систем. Основными этапами нечеткого вывода являются:
1. Фаззификация (определение значений) входных параметров, когда задаются «четкие» значения входных переменных, для которых вычисляются значения соответствующих функций принадлежности.
2. Формирование базы правил (базы знаний) системы нечеткого вывода, в основе которой лежат правила типа «если-то».
3. Агрегирование (композиция). На этом этапе строятся «усеченные» функции принадлежности переменной вывода, которые объединяются вместе, чтобы формировать одно нечеткое множество.
Построение усеченной функции принадлежности выходной переменной (треугольная функция fout(x)) показано на рис. 2. Функция принадлежности входной переменной обозначена как f2(x). Четкое значение входной переменной равно 2.
Подобное построение проводится для каждой входной переменной. Затем строится итоговое нечеткое множество для выходной переменной.
В алгоритме Мамдани объединение усеченных функций принадлежности переменной вывода производится с использованием операции МАКСИМУМ, если соответствующее правило соответствует логическому ИЛИ, и с использованием операции МИНИМУМ, если соответствующее правило соответствует логическому И (рис. 3).
4. Дефаззификация (приведение к четкости). На этом этапе получают четкое значение выходной переменной. Если используется центроидный метод, соответствующее значение равно х-координате центра тяжести фигуры, полученной на этапе 3 (на рис. 2 это значение равно 50).
В настоящее время подсистемы Fuzzy Logic входят в состав программного обеспечения многих современных систем вычислительной математики, например, Mathematica и Matlab. Среда Fuzzy Logic пакета прикладных программ Matlab является одним из наиболее удобных средств программирования в данной области. Основное преимущество данного подхода – использование визуального моделирования, когда достаточно сложные программы можно создавать без написания программного кода, который генерируется автоматически. Другим достоинством Matlab является возможность без написания программного кода (который генерируется автоматически) создать методами визуального моделирования компьютерную модель, например, в подпрограмме Simulink получить автоматическую генерацию С-кода, после «заливки» которого в микроконтроллер получить устройство, управляющее реальным техническим объектом.
Тем не менее использование Matlab содержит ряд недостатков:
Применяемый программный продукт является достаточно дорогим и имеет очень ограниченное число вариантов лицензирования.
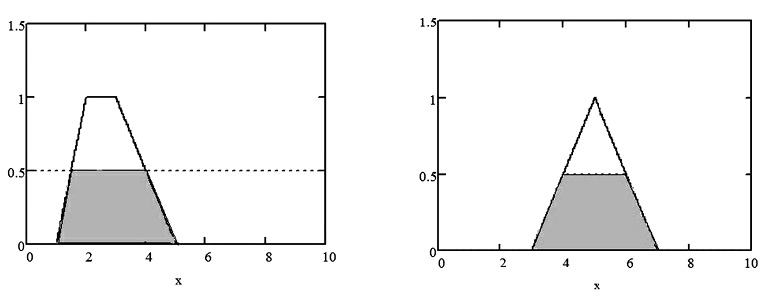
Рис. 2. Построение усеченных функций принадлежности
При создании программ можно использовать только алгоритм Мамдани или алгоритм Сугено.
Использование других алгоритмов требует достаточно сложных методов разработки, для которых Matlab не является наилучшей средой.
В настоящей работе мы в качестве среды моделирования выбран пакет прикладных программ Mathcad.
Модель зарядового устройства батареи на основе нечеткой логики
Рассмотрим упрощенную модель управления зарядовым устройством батареи, основанную на следующих предположениях [1]:
• устройство имеет два режима работы: режим подзарядки и режим быстрой зарядки;
• в режиме подзарядки в батарею поступает малое количество тока;
• в режиме быстрой зарядки весь доступный ток поступает в зарядное устройство;
• если батарея заряжена полностью, поступающий ток приводит к ее нагреву, поэтому если температура «высокая», следует перейти из режима быстрой зарядки в режим подзарядки;
• в режим подзарядки также следует перейти, если «высоким» стало напряжение батареи;
• если температура батареи «низкая» и напряжение также «низкое», следует перейти в режим быстрой зарядки.
Последние три правила формируют базу знаний системы управления устройством.
Для управления процессом зарядки введем две нечеткие переменные: «Напряжение» и «Температура». Нечеткая переменная «Температура» описывается терм-множеством {«Холодно (Cool)», «Тепло (Warm)», «Горячо (Hot)»}. График функции принадлежности для переменной «Температура» показан на рис. 3. Нечеткая переменная «Напряжение» описывается терм-множеством {«Низкое (Low)», «Среднее (Mid)», «Высокое (High)»}. Для описания этой переменной также использовались трапециевидные функции принадлежности с параметрами [0 0 5 10] (Low), [5 10 20 25] (Mid), [20 25 30 30] (High).
Выходной переменной (ChargeMode) является значение в интервале [0; 1], терм-множество которой {Fast (режим быстрой зарядки), Tricle (режим подзарядки)} характеризуется двумя трапециевидными функциями принадлежности с параметрами [0 0 0,4 0,6] и [0,4 0,6 1 1] соответственно. Разработчики должны определить границу значения выходной переменной, которое определяет переход из одного режима в другой. Например, можно считать, что следует перейти в режим подзарядки, если значение выходной переменной превышает 0,5.
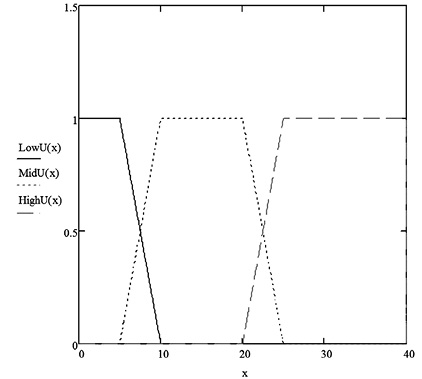
Рис. 3. Функции принадлежности переменной «Температура»
Пример вычислений показан на рис. 4. В качестве алгоритма нечеткой логики выбран алгоритм Мамдани. Четкое значение переменной вывода равно 0,744. В данном случае напряжение и температура являются достаточно высокими и следует перейти в режим подзарядки. Сравнение полученных результатов с аналогичными вычислениями в Matlab [3, 4] показывает идентичность полученных результатов.
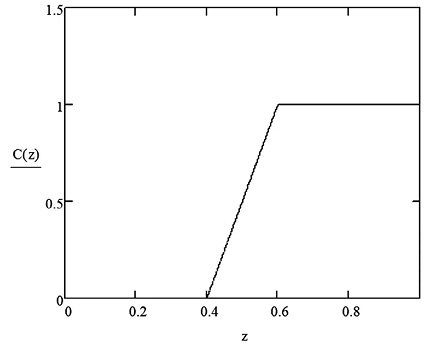
Рис. 4. Пример вычислений по алгоритму Мамдани
Рецензенты:
Мелик-Шахназаров В.А., д.ф.-м.н., ведущий научный сотрудник филиала ФГБУН «Институт кристаллографии им. А.В. Шубникова» Российской академии наук, научно-исследовательский центр «Космическое материаловедение», г. Калуга;
Коржавый А.П., д.т.н., профессор, зав. кафедрой «Промышленная экология и химия» Калужского филиала ФГБУ ВПО «Московский государственный технический университет им. Н.Э. Баумана», г. Калуга.
Работа поступила в редакцию 08.04.2013.
Библиографическая ссылка
Семененко М.Г., Черняев С.И., Черняев С.И. МОДЕЛИРОВАНИЕ СЛОЖНЫХ ТЕХНИЧЕСКИХ ОБЪЕКТОВ НА ОСНОВЕ ФОРМАЛИЗМА НЕЧЕТКОЙ ЛОГИКИ // Фундаментальные исследования. 2013. № 6-2. С. 291-294;URL: https://fundamental-research.ru/ru/article/view?id=31499 (дата обращения: 29.01.2026).



