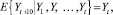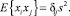Причины возникновения экономической нестабильности видится в самой структуре формирования и функционирования финансового рынка. Как отмечает В. Н. Якимкин, финансовые рынки, по сути, являются «громадной расчетной палатой, где работают взаимозачетные механизмы посредством соответствующих ценовых соотношений, с целью удовлетворения потребностей действующих на них субъектов» [3. С. 19]. Следовательно, мы можем предположить, что все рынки, входящие в финансовый рынок как некие подотрасли, являются системами, в которых масса участников взаимодействуют друг с другом и реагируют на внешнюю информацию с целью определения наилучшего состояния рынка для входа или выхода из экономической системы. В частности, инструменты на финансовом рынке могут иметь различную природу: это могут быть ценные бумаги, различающиеся по видам (акции, облигации), валюта, денежные активы или финансовые производные этих основных инструментов. Рассмотрев процедуру ценообразования на финансовом рынке, мы можем сделать предположение о его непредсказуемости. Это делает необходимым более детальное исследование структурных особенностей функционирования финансового рынка.
Предположим, что финансовый рынок представлен множеством финансовых инструментов, с которыми участники рынка постоянно проводят всевозможные операции. Это множество мы можем изобразить в виде временного ряда. Дальнейшее исследование такого временного ряда приведет нас к другому числовому ряду, который состоит из совокупности чисел, представляющих изменения цен финансовых активов за определенный период. Исследование данного ряда позволяет сделать вывод: цены на финансовые активы ведут себя в большей степени непредсказуемо. Как отмечают Р.Н. Мантенья и Г.Ю. Стенли, «при первом взгляде обнаруживается удивительный парадокс: динамические характеристики временного ряда, например отражающего цену финансового инструмента, в сущности, неотличимы от характеристик стохастического процесса» [1, С. 23]. Одна из основных причин такого поведения цен заключается в том, что механизм ценообразования на финансовом рынке предполагает значительное влияние рисковой составляющей. Практически все финансовые активы на любых рынках, подпадающих под действие законов финансового рынка, подвержены закономерностям функционирования арбитражной модели. Данная модель предполагает покупку и продажу одного и того же финансового актива с целью получения прибыли за счет разницы на различных финансовых рынках. Подобные сделки могут проходить как на одном рынке, так и на разных, причем эти рынки могут находиться в разных странах, что свидетельствует об интернационализации и глобализационных процессах на финансовом рынке. Такое поведение участников рынка приводит его участников к временному установлению эффективной цены.
Так, финансовый рынок в определенное время считался сверхэффективной рыночной системой. Однако сразу стоит отметить, что эффективность рынка в современных условиях и при существующих финансовых рынках является областью фантастики. Несмотря на то, что рынки являются очень сложными системами, аккумулирующими информацию о соответствующем активе в виде временных рядов цен, наибольшее распространение среди экономистов получила концепция, согласно которой рынки в высшей степени эффективны в части определений наиболее рациональных цен торгуемых активов. Данная гипотеза (гипотеза эффективного рынка) была представлена в середине 1960-х гг. Теоретической основой для теории эффективного рынка послужила работа Л. Башелье [7]. В дальнейшем эту тему исследовал П. Самуэльсон. В 1965 г. он сформулировал применимую к рыночным условиям гипотезу эффективного рынка и математически доказал, что ожидаемые цены изменяются случайным образом. Используя гипотезу рационального поведения трейдеров и учитывая рыночную эффективность, Самуэльсон смог продемонстрировать, что Yt+1 непосредственно связана с размерами цен Y0, Y1, Yt, причем связь этих величин можно описать следующим стохастическим процессом:
где E – доходность.
Однако, несмотря на то, что уравнение (1) предполагает следование вероятностному условию, цены на финансовом рынке также подвержены влиянию интуитивно-вероятностной модели справедливой игры. Это приводит к нестабильному изменению цен на финансовые активы. Так, в понимании игрока (инвестора) игра представляется справедливой, когда выигрыши и проигрыши взаимно компенсируются и уравновешивают друг друга. Например, ожидаемое накопление инвестора равно его текущим активам. Значит, вывод из данной формулы представляется таким, что любые ценовые изменения невозможно предсказать по подобному историческому ряду изменений цен за прошлые периоды. В середине ХХ столетия было проведено достаточное количество исследований, посвященных процессу изменения цен на финансовом рынке, которые показали, что корреляция цен в этом ракурсе очень мала.
В 1980-х гг. было доказано, что использование информации, представленной во временном ряде, может предсказывать прибыль в краткосрочной перспективе. Даже исследование временного ряда прибыль/цена или дивиденды не может давать точные данные о доходности актива.
Таким образом, эмпирические наблюдения и результаты исследования, теоретические разработки показывают с определенностью, что ценовые изменения на финансовом рынке трудно предсказать, если исходить только из данных временного ряда ценовых изменений. Иными словами, теория эффективных рынков не принесла ожидаемого результата.
Любой финансовый временной ряд выглядит непредсказуемо и, по сути, его будущие величины предсказать невозможно. Это не значит, что финансовый ряд ни на что не реагирует, что его цены никогда не могут измениться. Скорее наоборот – временной ряд цен на финансовом рынке и, как следствие, цены на финансовые активы несут в себе очень большой объем так называемой «несжимаемой» информации. В связи с этим существующий временной ряд имеет некоторые особенности:
– в связи с огромной информацией в данном ряду очень сложно, практически невозможно выделить влияние на цену фундаментальных экономических факторов (например, мы можем предположить, что цена финансового инструмента в большей степени зависит только от внутренних рыночных факторов, внешние факторы имеют небольшое значение);
– сложность предсказания цены актива связана не с недостатком информации, а скорее наоборот, с ее избытком;
– вся структура финансового рынка не предполагает хоть какой-нибудь привязки к реальному сектору экономики или корреляции с ним, что может являться причиной создания ценовых пузырей на рынке.
Единственным исключением из этого ряда может быть рынок тезавраций, состоящий из активов, которые прирастают в своей стоимости благодаря рыночным условиям, которые создаются на соответствующих рынках (рынок золота, алмазов, изумрудов), т.е. рынках драгоценных металлов и драгоценных камней. Хотя в последнее время динамика роста стоимости золота свидетельствует об очень большой доле «горячих» капиталов на данном рынке.
Возвращаясь к особенностям ценообразования финансовых активов, мы можем констатировать, что цены на активы формируются с учетом закономерностей случайного блуждания, а также на основании стохастических процессов Леви.
Например, финансовый рынок стремится к своей эффективности, при этом он стремится занять положение эффективного рынка. Эффективный рынок – это идеализированная система. Реальные финансовые рынки только приближенно эффективны. Мы можем только предполагать «идеальные» условия, т.е. существование совершенно эффективного рынка, и внутри данной парадигмы лишь развивать теории и проводить их эмпирическую проверку. Достоверность полученных данных будет напрямую зависеть от обоснованности сделанных предположений.
Например, концепция эффективного рынка применительно к финансовым рынкам будет иметь ценность при моделировании финансовых рынков. Приняв эти условия в качестве базовых, мы можем перейти к исследованию случайных процессов, наблюдаемых на финансовых рынках.
Например, для финансовых инструментов характерно возникновение различных рисков, связанных с биржевыми операциями. Ряд исследователей расценивают это как некую рискованную ситуацию [5].
Прежде всего, следует рассмотреть математические особенности экономического инструментария финансового рынка. Рассмотрим сумму n независимых переменных идентично распределенных случайных величин Xi:
Sn ≡ x1 + x2 + ... + xn. (2)
В данном случае Sn ≡ x(n∆t) следует рассматривать как сумму n случайных величин или как положение блуждающих частиц в момент времени t = n∆t , где n – количество сделанных единичных шагов; ∆t – временной интервал между соседними шагами. Так, аналогично распределенные случайные величины xi могут характеризоваться некими моментами 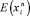 . Подобные величины не будут каким-либо образом зависеть от i.
. Подобные величины не будут каким-либо образом зависеть от i.
Простейшим примером случайного блуждания может быть распределение, осуществляемое при помощи случайных шагов размером s. В этом случае xi случайно может принимать значения +s или –s.
В частности, как первый, так и второй случаи для подобного процесса могут быть описаны следующим образом:
E(xi) = 0 и 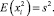 (3)
(3)
Проводя дальнейшие исследования мы придем к выводу, что для подобного случайного блуждания величина доходности Е может вычисляться следующим образом:
Из равенства (4) следует, если применить формулы предельного перехода, то доходность можно записать в вышеуказанном виде.
Так, нестабильность на финансовом рынке возникает как результат самовозрастающего процесса. Подобная особенность поведения цен на финансовом рынке характерна для любого сегмента финансового рынка. В частности, на рынке мы наблюдаем ситуацию случайного блуждания цен на финансовые активы. В зависимости от порядка определения цены на финансовый актив (в особенности это касается рисковой модели, которая влияет на ценообразование) цены на финансовом рынке подвержены хаотичному движению, имеющему зависимость далеко не от рыночных факторов.
В современной теории существуют известные методики определения риска:
1) VaRα(X);
2) CVaRα(X)
3) VaRe = VaRα(X – E(X));
4) CVaRe = CVaRα(X – E(X)) [155].
Данные методики используются для вычисления как риска отдельных финансовых активов, так и риска при инвестировании в портфели, составленные из активов, обращающихся на финансовом рынке. Мы вновь возвращаемся к особенностям финансовых активов, которые заключаются в асимметричном поведении активов на рынке, и к определению блуждающей величины доходности на финансовом рынке. Из равенства (4) мы можем получить формулу предельного перехода:
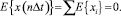 (5)
(5)
Далее выводим значение дисперсии случайного блуждания:
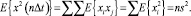 (6)
(6)
Теперь мы можем сделать вывод, что для случайного блуждания дисперсия любого процесса представляется в виде некого линейного процесса, который возрастает с увеличением количества шагов. Так, поведение цен можно рассмотреть как некий предельный переход случайного блуждания.
Предельный переход случайного блуждания на финансовом рынке может быть записан d виде некого стохастического инерционного процесса, который при условии n – ∞ и Δt nΔt будет стремиться к конечной величине. В этом случае мы можем сделать следующее преобразование:
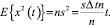 (7)
(7)
В этом случае мы имеем сходимость при n – ∞ и ∆t – 0 при s2 = D∆t , и в данном случае формула будет представлена следующим образом:
E{x2(t)} = Dt. (8)
Подобная линейная зависимость дисперсии s2(t) от t и представляется одной из типичных характеристик поведения цен на финансовом рынке. В подобной ситуации находятся практически все известные рыночные системы, где цены подвержены случайному блужданию [2, С. 57]. Не является исключением и финансовый рынок. Эта зависимость и есть один из видов диффузионного процесса, характеризующегося возможностью изменения цен на финансовых рынках. Данный стохастический процесс мы с полной уверенностью можем причислить к категории винеровских процессов [6].
Например, данное случайное блуждание цен на рынке можно описать в виде гаусовского процесса, т.е. на финансовом рынке применимо следующее утверждение: случайное блуждание эквивалентно гаусовскому процессу, т.е. хаотичному блужданию частиц. Подобное блуждание цен мы можем представить в виде определенного трендового процесса.
На разных рынках, входящих в финансовый рынок, мы видим неравномерность изменения, т.е. фактическое блуждание цен финансовых активов, все эти изменения представляются одной из составных частей гаусовского процесса.
В заключение следует отметить, что особенность формирования цен на финансовом рынке состоит в том, что обращающиеся на данном рынке активы изменяют цены в стохастическом порядке, который представляется характерным для функционирования гаусовского процесса. Эта особенность характерна для порядка ценообразования на любом финансовом рынке и является основной причиной нестабильности цен на финансовые активы.
Рецензенты:
Иваницкий В.П., д.э.н., профессор на кафедре финансовых рынков и банковского дела Уральского государственного экономического университета, г. Екатеринбург;
Марамыгин М.С., д.э.н., профессор, заведующий кафедрой финансовых рынков и банковского дела Уральского государственного экономического университета, г. Екатеринбург.
Работа поступила в редакцию 16.01.2013.
Библиографическая ссылка
Стрельников Е.В. ПРИЧИНЫ ВОЗНИКНОВЕНИЯ ЭКОНОМИЧЕСКОЙ НЕСТАБИЛЬНОСТИ НА ФИНАНСОВОМ РЫНКЕ // Фундаментальные исследования. 2013. № 6-1. С. 141-144;URL: https://fundamental-research.ru/ru/article/view?id=31431 (дата обращения: 22.01.2026).