Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Илюхин А.А. 1 Попов А.К. 1

---

1 ФГБОУ ВПО «Таганрогский государственный педагогический институт имени А.П. Чехова»

В рамках моментной теории упругости в перемещениях построено решение задачи об исследовании поведения цилиндрического тела в результате воздействия на него торцевых усилий. Построенная модель упругого равновесия цилиндрического тела в математическом отношении сведена к построению решения системы дифференциальных уравнений в частных производных. Определены компоненты тензора напряжений, моментных напряжений, изгиба-кручения, удовлетворяющих в области занятой телом, дифференциальным уравнениям равновесия при отсутствии массовых сил, формулам закона Гука, рассматриваемым в рамках моментной теории упругости псевдоконтинуума Коссера, а также граничным условиям на боковой поверхности и основаниях стержня. Найдено среднее значение кручения поперечного сечения цилиндрического тела, отличное от решений задач [6, 7], в которых среднее значение кручения не зависит от площади поперечного сечения стержня. Показано, что взаимосвязь крутки и величины S привносит именно учет моментных напряжений. Граничная задача определения неизвестной функции сведена к задаче Неймана для уравнения Пуассона. Доказана математическая непротиворечивость сделанных выводов.

Статья в формате PDF

2057 KB

моментная теория упругости

псевдоконтинуум Коссера

модель упругого равновесия цилиндрического тела

1. Аэро Э.Л., Кувшинский Е.В. Основные уравнения теории упругости сред с вращательным взаимодействием частиц // ФТТ. – 1960. – Т. 2. – С. 1399–1409.

2. Еремеев В.А., Зубов Л.М. Основы механики вязкоупругой микрополярной жидкости. – Ростов н/Д.: Изд-во ЮНЦ РАН, 2009. – 128 с.

3. Илюхин А.А., Попов А.К. Кручение стержня в рамках псевдоконтинуума Коссера // Вестник ТГПИ. – Таганрог: Изд. отдел ГОУВПО «ТГПИ», 2011. – № 1. – С. 43–50.

4. Илюхин А.А., Попов А.К. Растяжение микрополярного естественно закрученного стержня // Научно-технический вестник Поволжья. – Казань, 2011. – № 6.

5. Илюхин А.А., Тимошенко Д.В. Математическая модель замкнутых молекул ДНК // Известия Саратовского университета. – 2008. –Т.8. – Вып. 3. – С. 32–40.

6. Лурье А.И., Джанелидзе Г.Ю. Задача Сен-Венана для стержней, близких к призматическим // ДАН СССР. – 1939. – т. XXIV. – № 1–№ 3.

7. Риз П.М. Деформация естественно закрученных стержней // ДАН СССР. – 1939. – Т. 3, № 4. – С. 451.

8. Шкутин Л.И. Численный анализ разветвленных форм изгиба арок // Прикладная механика и техническая физика. – 2001. – Т. 42, № 4. – С. 155–160.

При расчете напряженно-деформированного состояния, в том числе исследовании устойчивости конфигураций упругих тел и упруго-вязких жидкостей [1, 8] необходимо учитывать вращательное взаимодействие частиц. Общие теоретические положения моментной теории упругости начали разрабатываться со времен братьев Коссера и повторный интерес к описанию деформации тел на основе континуума Коссера в научных публикациях проявился во второй половине 20 века. В монографии В.А. Еремеева и Л.И. Зубова [2] достаточно полно описана история развития этого раздела теории упругости и приведены обширные литературные обзоры, указаны области приложения, в частности, при анализе устойчивости. В работе [5] показано, что учет моментных напряжений увеличивает жесткостные характеристики упругого тела и, естественно, в критических ситуациях может оказать существенное влияние на поведение упругого элемента. В рамках механической модели ДНК учет вращательных взаимодействий привел к достаточному совпадению конфигураций ДНК, полученных с помощью построенной в работе теории и тех, которые получены в ряде экспериментальных работ с помощью фотографирования с использованием электронных микроскопов. При определении рабочих характеристик элементов ряда точных приборов, нанотрубок, работающих в условиях упругой деформации, как показывает практика расчетов, должно учитываться вращательное взаимодействие их частиц.

Постановка задачи. Решение пространственных задач теории упругости нередко сводится к решению одной из канонических задач, к числу которых относятся задачи, описывающие деформацию призматических тел концевыми нагрузками. Одним из математических достоинств таких задач является возможность сведения ее к плоской задаче теории упругости. Кроме того, эти задачи представляют самостоятельный научный и практический интерес. Авторам работы не удалось найти как в монографиях, так и в научных статьях, решение этой задачи. Поэтому в данной работе предпринята попытка аналитического построения исследуемой задачи с целью восполнить пробел в исследовании деформации такого класса тел.

Пусть призматическое тело длиной L закреплено одним концом, а на свободном конце несет нагрузку, статически эквивалентную силе Р, перпендикулярную к оси тела, приложенную в произвольной точке торцевого сечения. Массовые силы и силы на боковой поверхности тела отсутствуют. Начало координат поместим в произвольной точке торцевого сечения. При этом ось направим параллельно оси тела, а ось – параллельно силе Р. Сечение исследуемого стержня предполагается односвязным. Задача об упругом равновесии стержня при указанных условиях сводится к нахождению компонент тензора напряжений и моментных напряжений μij, удовлетворяющих в области занятой телом, дифференциальным уравнениям равновесия при отсутствии массовых сил, формулам закона Гука, рассматриваемым в рамках моментной теории упругости, а также граничным условиям на боковой поверхности и основаниях стержня.

Решение в перемещениях поставленной задачи будем искать в виде:

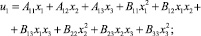
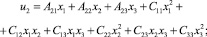(1)

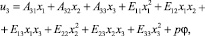
где φ(x1, x2) – некоторая функция, подлежащая определению, p = P/S.

Основные кинематические соотношения, закон Гука и уравнения равновесия в рамках моментной теории упругости представлены в виде [3]:

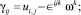
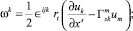
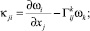
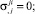
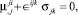(2)

где ui, ωk – ковариантные компоненты вектора перемещений и микроповорота; γij, κji, σij, μij – компоненты тензоров деформации, изгиба-кручения, силовых и моментных напряжений; 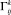– символы Кристоффеля второго рода; ∈skt – компоненты тензора Леви-Чивиты.

Решение поставленной задачи производится в декартовой прямоугольной системе координат. В результате кинематические соотношения (2) могут быть преобразованы к виду:

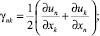
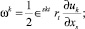
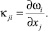(3)

Для того чтобы удовлетворить двум группам уравнений равновесия:

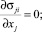
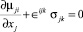, (4)

определим с учетом (1) значения компонент симметричного тензора деформаций:

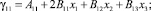
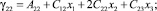
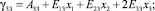
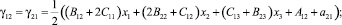(5)

;

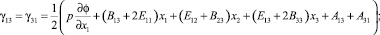
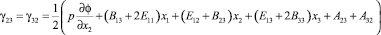тензора изгиба – кручения:

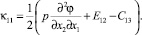
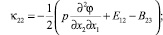
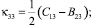
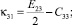(6)

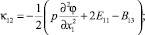
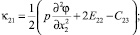
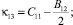
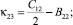
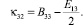
Если среда изотропная, то закон Гука принимает вид:

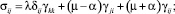
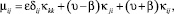(7)

где δij – символы Кронекера.

Учитывая значения компонент тензора деформаций (5) и первое равенство закона Гука (7), получим соответствующие значения компонент тензора силовых напряжений:

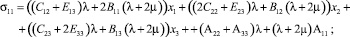
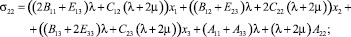
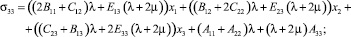
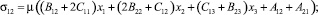
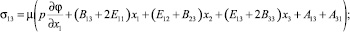
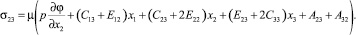(8)

С учетом значения компонент псевдотензора изгиба-кручения (4) компоненты тензора моментных напряжений, получаемые из закона Гука (8), представимы в виде:

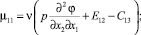
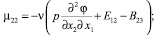
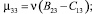
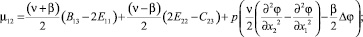
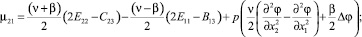
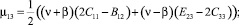
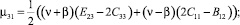
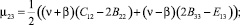
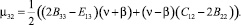(9)

Первая группа уравнений равновесия (4) с учетом значений компонент тензора напряжений (8) и (9), преобразуется к виду:

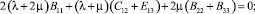
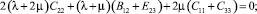
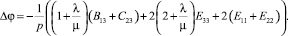(10)

Аналогично записывается вторая группа уравнений равновесия (4):

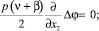
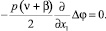(11)

Третье уравнение второй группы уравнений равновесия (4) удовлетворяется тождественно.

Запишем граничные условия на основании x3 = L цилиндрического тела:

V1 = P; M1 = M2 = M3 = 0.

На основании вышеприведенных формул можно получить:

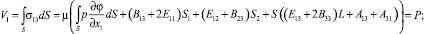
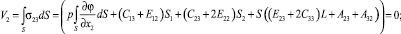(12)

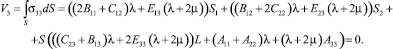
Граничные условия на основании x3 = 0 цилиндрического тела:

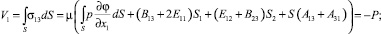
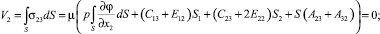(13)

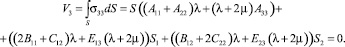
Из равенств (12) и (13) выполняются следующие равенства:

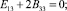
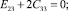
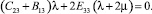(14)

Вычислив компоненты моментов внутренних сил в поперечном сечении, граничные условия (13) можно записать в виде:

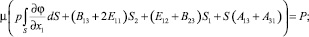
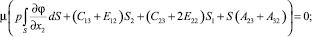
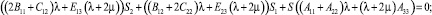
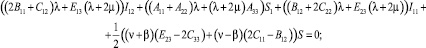
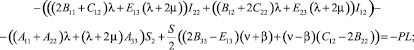
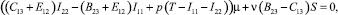(15)

где 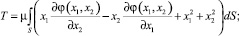; S1 и S2 – статические моменты поперечного сечения стержня относительно осей x1 и x2; I11, I22 и I12 – моменты инерции сечения.

Компоненты единичного вектора нормали к боковой поверхности:

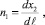
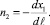
Запишем граничные условия на боковой поверхности стержня с прямолинейной осью:

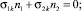
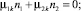k = 1, 2, 3. (16)

Учитывая независимость переменных x1, x2, x3,, друг от друга, константы, стоящие при соответствующих независимых переменных, также приравняем нулю:

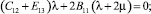
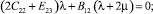
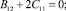
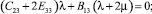
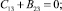
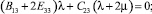
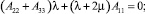
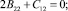(17)

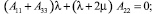
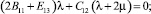
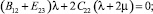
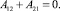
Третье равенство первой группы граничных условий на боковой поверхности стержня (16) с учетом равенства (17) представляется в виде условия Неймана:

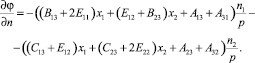(18)

Аналогично для тождественного удовлетворения третьего равенства второго уравнения (16) компоненты тензора моментных напряжений μ13, μ23, достаточно положить равными нулю. Константы, стоящие при независимых переменных, также приравняем нулю:

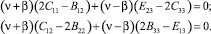(19)

Проинтегрируем первые два равенства второго уравнения (16) вдоль контура L:

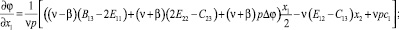(20)

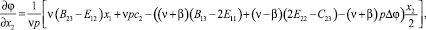
где c1, c2 – константы, возникающие в результате интегрирования.

Условия Неймана (20), полученные из второй группы граничных условий, должны совпадать с условиями Неймана, полученными из первой группы граничных условий (18). Приравняем коэффициенты, стоящие при соответствующих переменных:

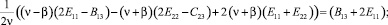
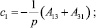
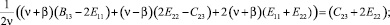(21)

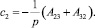
Интегрируя равенства (20) вдоль контура L и применяя формулу Остроградского, получим:

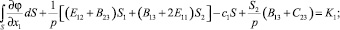
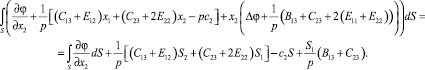
Преобразуем последние уравнения с учетом условия Неймана (20):

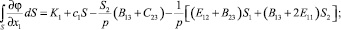
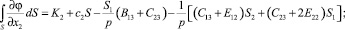
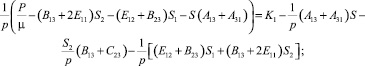
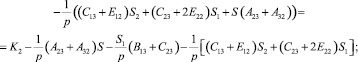
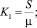K2 = 0 (22)

Из равенств (10), (14), (15), (17), (19), (21), (22) получаем взаимосвязи между константами:

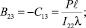
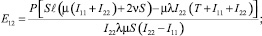(23)

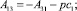
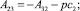
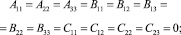
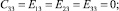
С учетом взаимосвязи (23) между константами третье уравнение (10) преобразуется к виду:

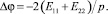(24)

Таким образом, граничная задача определения функции φ(x1, x2), является задачей Неймана (10) для уравнения Пуассона (24). Константы E11, E22, и их сумма E11 + E22 должны быть отличны от нуля, иначе решение поставленной задачи в перемещениях, представимое в виде (1), приведет к противоречиям, заключающимся в том, что константа K1 равна нулю.

В результате найденные компоненты вектора перемещений приобретают вид:

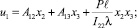
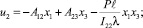
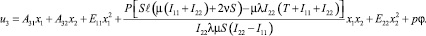
Выпишем выражения для компонент симметричного тензора силовых напряжений:

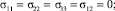
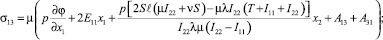
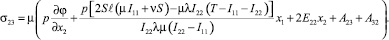
и компонент тензора моментных напряжений:

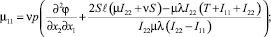
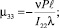
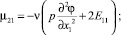
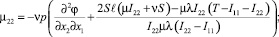
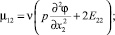
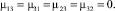
Выводы. В сравнении со случаями исследования прямолинейного стержня [6, 7] депланацию поперечного сечения стержня вызывают не только компоненты тензора силовых напряжений σ13, σ23, но и компоненты тензора моментных напряжений μ11, μ22, μ12, μ21.

Среднее значение кручения поперечного сечения определяется формулой:

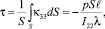(25)

из которой можно сделать вывод, что τ зависит от p и геометрических характеристик стержня (длины стержня L и осевого момента инерции I22) и не зависит от формы поперечного сечения тела. Значит, под действием силы P стержень будет закручиваться в направлении от оси Ox2 к оси Ox1, о чем и говорит минус, стоящий в формуле (25). Заметим, что в формуле (25), для p = 0 – τ равно нулю. В сравнении со случаем кручения прямолинейного стержня [3], в рамках которого среднее значение кручения τ зависит от крутящего момента Mk, аналога геометрической жесткости при кручении T, в исследуемой задаче τ зависит, в том числе, и от площади поперечного сечения стержня S: 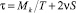. Следовательно, взаимосвязь крутки τ и величины S привносит именно учет моментных напряжений. Как и в случае кручения [3] и растяжения [4] микрополярного естественно-закрученного стержня:

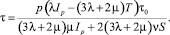
Данная статья написана при финансовой поддержке государственного задания Министерства образования и науки РФ ФГБОУ ВПО «ТГПИ имени А.П. Чехова» по проекту № 1.1885.2011, тема: «Математическое моделирование статики и динамики гибридных механических систем и идентификация их параметров», научный руководитель – Илюхин Александр Алексеевич.

Рецензенты:

Куповых Г.В., д.ф.-м.н., профессор, заведующий кафедрой физики Технологического института Южного федерального университета, г. Таганрог;

Антонов А.В., д.т.н., профессор, декан факультета кибернетики Обнинского института атомной энергетики Национального исследовательского ядерного университета МИФИ Министерства образования и науки Российской Федерации, г. Обнинск.

Работа поступила в редакцию 19.03.2012.

Библиографическая ссылка