Одной из общих закономерностей разрушения твердых тел является существование временной зависимости прочности [1]. При замедленном разрушении стали зарождение и развитие трещины являются термически активированными процессами [1–3]. Сталь, в которой присутствуют остаточные внутренние микронапряжения, например, обладает запасом неравномерно распределенной по объему упругой энергии с ними связанной, даже без приложения внешней нагрузки. Полагали, что остаточные микронапряжения в локальных областях перед вершинами кристаллов мартенсита могут понижать энергию, необходимую для достижения энергетического барьера разрыва атомных связей [6, 7].
Целью работы являлась разработка кинетической модели прочности, описывающей переход от микромеханизма замедленного разрушения к микромеханизму скола мартенситной стали, учитывающей уровень остаточных микронапряжений, скорость нагружения и температуру испытаний.
Кинетика термофлуктуационного замедленного разрушения закаленной стали
Основная формула (1) кинетической теории [1]:
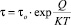 (1)
(1)
устанавливает связь времени до разрушения τ с энергией активации Q, где τo – предэкспоненциальный множитель, зависящий от частоты попыток преодоления потенциального барьера, количества мест активации и их характеристик; К – постоянная Больцмана; Т – температура. Разрушение связывают с накоплением разрывов атомных связей в результате термофлуктуационных колебаний атомов [1].
Согласно кинетической теории прочности для полимерных материалов [1] время до разрушения при действии напряжения определяется формулой (2):
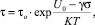 (2)
(2)
где Uo – энергетический барьер; γ – активационный объем; σ– напряжение в зоне разрушения.
Эта модель предполагает аддитивность напряжений разной природы в материале независимо от причин их вызвавших. Для случая неравномерного распределения локальных напряжений в образце с надрезом [2] в выражение (2) необходимо подставить значение максимального локального растягивающего напряжения σ11max (3):
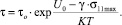 (3)
(3)
Энергия активации в случае отсутствия остаточных внутренних микронапряжений (4) зависит от величины напряжений, вызванных приложением нагрузки извне:
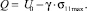 (4)
(4)
Однако наличие в мартенситной стали локальных остаточных внутренних микронапряжений приводит к появлению локальных областей в вершинах мартенситных кристаллов с повышенной потенциальной энергией [2, 3, 6]. В этом случае, энергия активации равна разности энергии барьера и потенциальной энергии активационного объема (5):
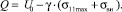 (5)
(5)
Время до зарождения трещины в закаленной стали при одновременном воздействии остаточных внутренних микронапряжений σвн и действии σ11max соответственно равно (6):
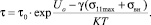 (6)
(6)
Энергия барьера Uo может быть оценена как (7):
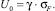 (7)
(7)
Тогда время до зарождения трещины в стали с остаточными микронапряжениями может быть определено по формулам (8), (9) с учетом параметров кинетической теории прочности (К, Т, τ0, γ) и силовыми параметрами микромеханики разрушения (σF, σ11max):
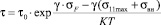 (8)
(8)
или
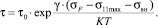 (9)
(9)
Заметим, что при τ = τ0, числитель равен нулю, а γ≠ 0,, тогда σF = σ11max + σвн, что можно рассматривать как нетермоактивируемое зарождение трещины – силовой подход.
Был рассмотрен и другой (энергетический) подход к описанию кинетики замедленного разрушения закаленной стали. Полагали, что остаточные внутренние микронапряжения в вершинах кристаллов мартенсита участвуют в процессе локального разрушения не аддитивно по отношению к локальным растягивающим напряжениям, вызванным внешними нагрузками и концентрацией напряжений. То есть, они участвуют в разных микромеханизмах и на разных этапах зарождения трещины. Энергия активации Q в формуле (1) может быть представлена как разность энергии барьера Uo и потенциальной энергии от напряжений (10), (11), вызванных внешней нагрузкой U(σ11max) и остаточными внутренними микронапряжениями U(σвн)():
Q = U– U(σвн) – U(σ11max) (10)
или
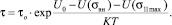 (11)
(11)
Рассмотрим гипотетический случай силового разрушения при действии напряжения от внешней нагрузки в течение времени τ = τ0, тогда энергия активации Q равна нулю:
U – U(σвн) – U(σ11max) = 0. (12)
Тогда, с учетом предположения, что 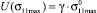 получим (13):
получим (13):
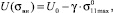 (13)
(13)
где 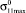 соответствует величине σ11max, при которой действует только силовой механизм разрушения (τ = τ0).
соответствует величине σ11max, при которой действует только силовой механизм разрушения (τ = τ0).
Подставив в (10) выражение (13), определили энергию активации в виде (14):
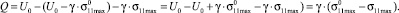 (14)
(14)
Тогда время до зарождения трещины можно представить в виде (15):
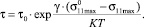 (15)
(15)
Полагали, что значение 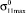 по физическому смыслу и по величине соответствует характеристике сопротивления материала локальному разрушению σF – критическому локальному напряжению (напряжению скола) (16):
по физическому смыслу и по величине соответствует характеристике сопротивления материала локальному разрушению σF – критическому локальному напряжению (напряжению скола) (16):
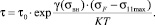 (16)
(16)
Таким образом, с точки зрения кинетической теории прочности в зависимости от исходных предпосылок были получены две гипотезы: одна (силовая) – формула (9) – рассматривает роль остаточных микронапряжений и локальных напряжений от внешней нагрузки в механизме локального разрушения как аддитивную, другая (энергетическая) – формула (16) ‒ как не аддитивную.
Материалы и методы эксперимента
Для проверки первой и второй гипотез были проведены экспериментальные исследования. Исследовали сталь 18Х2Н4ВА (0,19 С; 1,5 Cr; 4,1 Ni; 0,20 Si; 0,37 Mn; 0,82 W; 0,003 S; 0,003 P вес. %), выплавленную в открытой индукционной печи на основе карбонильного железа. Использовали образцы 10×10×55 мм с острым надрезом Шарпи. С целью получения состояний, различающихся уровнем остаточных внутренних микронапряжений, использовали термообработку: закалка 950 °С, вода, отдых 15; 2700; 4600; 8700 мин и низкотемпературный отпуск 100 °С, 2 ч. Образцы перед термообработкой вакуумировали в кварцевых колбах с целью избежать обезуглероживания поверхностных слоев при закалке.
Изучение влияния температуры испытаний и скорости нагружения на склонность к замедленному разрушению закаленной стали проводили сосредоточенным изгибом при различных скоростях движения траверсы испытательной машины от 0,01 до 10 см/мин при различных температурах испытания от 77 до 293 К. С помощью метода конечных элементов [2] приложенную нагрузку пересчитывали в максимальные локальные растягивающие напряжения σ11max в зоне локального разрушения перед концентратором напряжений вблизи границы упругой и пластической зон. Предел текучести, показатель и коэффициент упрочнения, необходимые для расчета локальных напряжений σ11max методом конечных элементов, определяли по результатам испытаний на растяжение гладких образцов МРГ-3 диаметром 4,3 мм [2]. Строили кривые замедленного хрупкого разрушения в координатах: логарифм времени до зарождения трещины – максимальное локальное растягивающее напряжение σ11max (рис. 1).
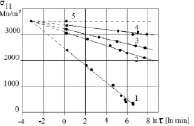
Рис. 1. Кривые замедленного хрупкого разрушения стали 18Х2Н4ВА в закаленном состоянии после различного времени отдыха: 1 – 15; 2– 2700; 3 – 4600; 4 – 8700 мин; 5 – отпуск 100 °С, 2 ч
Зависимости разрушающих максимальных локальных растягивающих напряжений σ11max от скорости нагружения и температуры испытаний (77–293 К) стали с различными уровнями остаточных внутренних микронапряжений представлены на рис. 2 и 3.
Экспериментальные результаты и их обсуждение
Влияние температуры испытаний и скорости нагружения на склонность к замедленному разрушению стали
В том случае, если справедлива первая гипотеза модели замедленного разрушения (9), то при τ = τ0, т.е. при силовом механизме локального разрушения, должно выполняться условие (17), (18):
σF – σ11max – σвн (17)
или
σF = σ11max + σвн. (18)
Это означает, что при τ = τ0 для разных кривых замедленного разрушения τ = f(σ11max, σвн), соответствующих различным уровням остаточных микронапряжений σвн, пересечения кривых в одной точке, т.е. точки «полюса», быть не может. Поэтому следует заключение, что первая гипотеза (9) не подходит для кинетической теории замедленного разрушения стали.
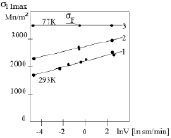
Рис. 2. Влияние скорости нагружения на локальное напряжение в месте зарождения трещины в свежезакаленной стали 18Х2Н4ВА: 1 – 283 К; 2 – 170 К; 3 – 77 К; ¡ – отдых 30 мин; ¢ – отпуск 100 °С, 2 ч
Вторая гипотеза (16), напротив, хорошо подтверждается экспериментом. Полученные экспериментальные зависимости ln τ = (σ11max) для замедленного разрушения стали с различными уровнями остаточных внутренних микронапряжений хорошо описываются выражением (16).
Таким образом, эксперименты подтвердили, что для описания кинетики замедленного разрушения справедлива вторая гипотеза.
Было установлено (рис. 3), что ниже 77 К разрушающее σ11max стали с высоким уровнем остаточных внутренних микронапряжений не зависит от скорости нагружения для разных уровней остаточных внутренних микронапряжений, т.е. остаточные внутренние микронапряжения не дают вклада в напряжение зарождения трещины. В предельном случае, при достаточно низкой температуре образование зародышевой трещины происходит по достижении локальным напряжением σ11max критического значения σF по силовому безактивационному механизму.
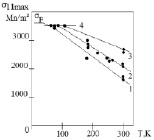
Рис. 3. Влияние температуры на напряжение зарождения трещины в свежезакаленной (отдых 30 мин) 1–3 и низкоотпущенной (¢ – отпуск 100 °С, 2 ч) – 4 стали 18Х2Н4ВА при различных скоростях нагружения: 1 – 0,01; 2 – 0,5; 3 – 10 см/мин
Переход от термофлуктуационного замедленного разрушения к хрупкому разрушению сколом
Преобразуем уравнение (16), выразив напряжение сопротивления сколу σF в явном виде (19)–(21):
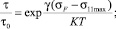 (19)
(19)
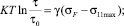 (20)
(20)
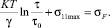 (21)
(21)
Полученное выражение (21) представляет критериальное условие зарождения трещины. Это уравнение показывает, что для достижения критериального значения прочности материала σF необходимо сочетание термоактивационной компоненты 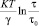 и локального напряжения σ11max. При замедленном термоактивированном разрушении преобладает термоактивационная компонента, а силовая компонента σ11max не достаточна для разрушения сколом σ11max < σF. В результате, реализуется механизм замедленного разрушения, зависящий от температуры и реализуемый за время τ.
и локального напряжения σ11max. При замедленном термоактивированном разрушении преобладает термоактивационная компонента, а силовая компонента σ11max не достаточна для разрушения сколом σ11max < σF. В результате, реализуется механизм замедленного разрушения, зависящий от температуры и реализуемый за время τ.
В том случае, когда локальное напряжение σ11max приближается к значению σF, роль термоактивационной компоненты в зарождении трещины уменьшается и происходит переход к силовому механизму хрупкого разрушения – сколу. При значительных скоростях нагружения (при малых τ) σ11max достигает σF, тогда происходит разрушение сколом.
Выводы
1. Предлагается кинетическая модель замедленного разрушения закаленной стали, описывающая зависимость времени до зарождения трещины от остаточных внутренних микронапряжений, сопротивления сколу, уровня приложенного локального напряжения и температуры испытаний (16).
2. Условия перехода от термически активированного механизма при замедленном разрушении к силовому для локального разрушения закаленной стали могут быть описаны критериальным выражением (21), состоящим из суммы активационной и силовой компонент равных характеристике сопротивления стали локальному разрушению (сколу). Условия этого перехода зависят от уровня остаточных микронапряжений, времени (скорости) нагружения и температуры испытаний.
Рецензенты:
Янукян Э.Г., д.ф.-м.н., декан инженерного факультета, Северо-Кавказский федеральный университет, г. Пятигорск;
Казуб В.Т., д.т.н., профессор, зав. кафедрой физики и математики Пятигорской государственной фармацевтической академии, г. Пятигорск.
Работа поступила в редакцию 07.03.2013.
Библиографическая ссылка
Шиховцов А.А., Мишин В.М. КИНЕТИКА И МИКРОМЕХАНИКА ЗАМЕДЛЕННОГО РАЗРУШЕНИЯ СТАЛИ // Фундаментальные исследования. 2013. № 4-4. С. 858-861;URL: https://fundamental-research.ru/ru/article/view?id=31286 (дата обращения: 16.12.2025).



