При понижении температуры в условиях нагружения стальные детали на сравнительно небольшом температурном интервале – пороге хладноломкости – интенсивно теряют механические свойства [1]. На этом интервале резко падают разрушающая нагрузка и предел прочности. При температурах ниже этого интервала разрушение происходит без остаточной макропластической деформации. На переход от вязкого к хрупкому указывают изменения строения излома и резкое снижение ударной вязкости, наблюдаемое в диапазоне граничных значений вязкого и хрупкого разрушения. При снижении температуры создаются условия, затрудняющие пластическую деформацию, поэтому образование пластической зоны в основании надреза или трещины будет задерживаться. Таким образом, понижение температуры является основным фактором, приводящим к охрупчиванию стали.
Целью данной работы являлась разработка физико-механических основ критерия хладноломкости (вязко-хрупкого перехода), который бы учитывал характеристики сопротивления металла деформации и разрушению, а также основной комплекс совокупно действующих факторов (внешних и внутренних), ответственных за переход стального образца или детали из вязкого состояния в хрупкое. Такой температурный критерий позволил бы прогнозировать температуру хладноломкости образцов произвольной формы или деталей с концентраторами напряжений по результатам испытаний стандартных образцов. Полагали, что в основу механизма такого температурного критерия может быть положен критерий локального разрушения – сопротивление сколу ϬF (критическое максимальное локальное растягивающее напряжение), инвариантное (независимое) к таким внешним факторам, как геометрия концентраторов напряжений и образцов, скорость нагружения и температура испытаний [1-4].
Установление теоретической связи температуры хладноломкости с внутренними характеристиками стали – сопротивления сколу σF, пластичности σT и внешними условиями (скорость нагружения и геометрия концентратора напряжений)
При хрупком разрушении сколом микротрещина зарождается под воздействием сдвиговых напряжений, однако локальное разрушение в целом контролируется величиной максимального локального растягивающего напряжения σ11max перед концентратором напряжений, где напряжение может превосходить предел текучести. Известную схему Иоффе можно развить, рассматривая пересечение характеристики стали хрупкому разрушению – уровня сопротивления сколу (σF), независящего от температуры, скорости нагружения и геометрии образцов и концентраторов напряжений [1, 2], и температурных зависимостей максимального локального растягивающего напряжения (σ11max) перед концентратором напряжений (рис. 1).
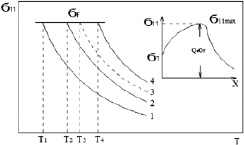
Рис. 1. Схема влияния перенапряжения на критическую температуру хрупкости:1 – гладкий образец; 2 – образец с U-надрезом; 3 – образец с V-надрезом; 4 – образец с трещиной
Согласно этой схеме хрупкое разрушение реализуется при достижении максимальным локальным растягивающим напряжением перед надрезом (σ11max) уровня сопротивления сколу (σF). Из рис. 1 видно, что температура хладноломкости (Т1, Т2, Т3, Т4) зависит от остроты концентратора напряжений. Эта температура (Tкp), в дальнейшем называемая температурой хладноломкости, феноменологически соответствует температуре, при которой нагрузка общей текучести Рот достигает разрушающей нагрузки Рр (рис. 1):
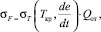 (1)
(1)
где Qoт – перенапряжение общей текучести образца с концентратором напряжений.
Перенапряжение Q xарактеризует превышение максимальным локальным растягивающим напряжением предела текучести стали. При некотором уровне нагрузки – нагрузке общей текучести Рот, рост σ11max за счет стеснения деформации прекращается и перенапряжение достигает своего максимального значения Qoт [5].
Можно выразить зависимость предела текучести σT = f(T, de⁄dt) от температуры испытаний (Т) и скорости нагружения (de/dt):
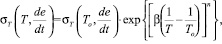 (2)
(2)
где σT = f(T, de⁄dt) – предел текучести при комнатной температуре, определенный при скорости нагружения (de/dt), Тo = 293 К; β, n – коэффициенты, зависящие от типа стали.
Выразив критическую температуру хрупкости явным образом из (1), получили зависимость Ткр = (σF; σT; Qoт), учитывающую влияние сопротивления разрушению (σF), текучести (σT) (зависящей от скорости нагружения (de/dt)) и геометрии образца, концентратора напряжений и способа нагружения (Qoт):
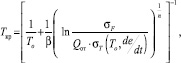 (3)
(3)
где β, n – коэффициенты связи предела текучести с температурой, зависящие от марки стали и приведенные в известных справочниках; To – нормальная температура (20 °С); σT – предел текучести при нормальной температуре (To).
Полученное теоретическое выражение (3) дает возможность расчетом определить критические температуры хрупкости (Ткр) стальных образцов или деталей с концентраторами напряжений различных типов.Для этого необходимо из эксперимента знать критическое максимальное локальное напряжение (σF), предел текучести стали (σT) при комнатной температуре (To), определенный при скорости нагружения, равной скорости нагружения зоны локального разрушения детали, коэффициенты n и β и перенапряжение общей текучести исследуемого образца или детали (Qoт), рассчитанное методом конечных элементов.
Материал и методы исследования
Исследования проводили на стали 10 кп, выплавленной в открытой индукционной печи. Использовали образцы на растяжение диаметром 8,00 мм гладкие и с кольцевыми проточками глубиной 2,00 мм, углами раскрытия 30, 60, 120° и U-образными. Термообработку проводили по режиму: нагрев 1000 °С, 60 мин, охлаждение на воздухе. Размер зерна после такой термообработки составлял 30 мкм. Испытания проводили растяжением на испытательной машине «Instron» при скоростях нагружения 2,20 и 200 мм/мин и различных температурах испытания в диапазоне от 77 до 293 К. Регистрировали разрушающую нагрузку Рр и нагрузку общей текучести Рот.. По результатам испытания гладких образцов определяли температурную зависимость предела текучести при скорости нагружения 2,20 и 200 мм/мин. Далее определяли температуру хладноломкости как температуру совпадения этих нагрузок и соответствующий ей предел текучести.
Экспериментально критическое максимальное локальное растягивающее напряжение σF определяли по испытаниям образцов с U-образным надрезом при скорости нагружения 2,20 и 200 мм/мин. Экспериментальное определение критических температур хрупкости заключалось в установлении температуры, при которой нагрузка общей текучести равна разрушающей нагрузке.
С другой стороны, вычисляли по формуле (3) температуры хладноломкости для образцов на растяжение с надрезами различной геометрии: углами раскрытия 30, 60, 120° и скоростями нагружения 2, 20 и 200 мм/мин.
Результаты исследования и их обсуждение
Подтверждение инвариантности критерия локальных растягивающих напряжений. Полагали необходимым подтвердить инвариантность критерия локальных растягивающих напряжений [1, 3, 4], а именно независимость сопротивления сколу σF (критического максимального локального растягивающего напряжения) от таких внешних факторов, как геометрия концентраторов напряжений и образцов, скорость нагружения и температура испытаний.
а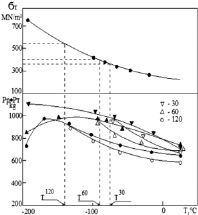 б
б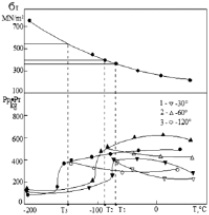
Рис. 2. Зависимости разрушающей нагрузки, нагрузки общей текучести и предела текучести от температуры испытаний образцов с различной геометрией надрезов (углы раскрытия 120, 60 и 30° при скорости нагружения: а – 20 мм/мин; б – 200 мм/мин. Сталь 10 кп
По результатам испытаний и расчета критических максимальных локальных растягивающих напряжений была построена их зависимость от температуры испытаний, угла раскрытия надреза, скорости нагружения (рис. 3).
а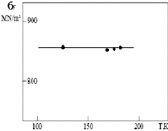 б
б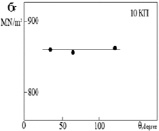 в
в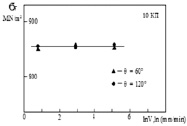
Рис. 3. Независимость критических максимальных локальных растягивающих напряжений σF от а – температуры испытаний; б – угла раскрытия надреза, скорости нагружения. Сталь 10 кп
Установлено экспериментально, что критическое максимальное локальное растягивающее напряжение σF не зависит от температуры испытаний, угла раскрытия надреза и скорости нагружения для стали 10 кп, что подтверждают результаты, полученные Ужиком Г.В., Ноттом Д.Ф., Орованом Е., Мешковым Ю.Я. [1, 3, 5]. Таким образом, в основу критерия хладноломкости может быть положен критерий локального разрушения – сопротивление сколу σF (критическое максимальное локальное растягивающее напряжение), инвариантное к геометрии концентраторов напряжений и образцов, скорости нагружения и температуре испытаний.
Проведена экспериментальная проверка теоретической связи температуры хладноломкости с внутренними характеристиками стали – локальной прочности (сопротивления сколу σF), пластичности (σT) и внешними условиями (скорость нагружения и геометрия концентратора напряжений).
Результаты экспериментального и расчетного определения критической температуры хрупкости представлены на рис. 4.
Из рис. 4 видно, что увеличение остроты надреза приводит к смещению температуры хладноломкости в область повышенных температур. Так, при одной и той же скорости нагружения уменьшение угла раскрытия надреза с 120 до 30° приводит к значительному повышению температуры хладноломкости. Увеличение скорости нагружения с 2 до 200 мм/мин также приводит к значительному повышению температур хладноломкости.
Расчетные температуры хладноломкости образцов с различными геометриями надрезов (углами раскрытия 120, 60, 30°), определенные по формуле (3), сравнивали с экспериментально определенными температурами хладноломкости. Сравнение расчетных и экспериментально определенных температур хладноломкости образцов с различными концентраторами напряжений, представленное на рис. 4, показывает хорошую сходимость теоретических и экспериментальных результатов и возможность прогнозирования температур хладноломкости образцов или деталей с учетом их геометрии и скорости нагружения по результатам испытаний стандартных образцов по формуле (3).
а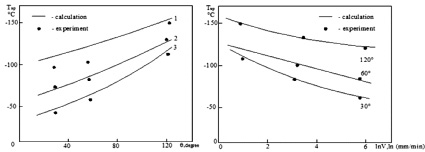 б
б
Рис. 4. Расчетные и экспериментально определенные зависимости температуры хладноломкости от: а – углов раскрытия надрезов (120, 60 и 30°); б – скорости нагружения (2,20 и 200 мм/мин). Сталь 10 кп
Заключение
1. Разработаны физико-механические основы критерия хладноломкости (вязко-хрупкого перехода), заключающиеся в том, что температура хладноломкости, определяемая как температура достижения критического состояния – локального разрушения в вершине конструктивного концентратора напряжений, непосредственно связана с характеристиками прочности, текучести и перенапряжения. Этот температурный критерий позволяет прогнозировать температуру хладноломкости образцов произвольной формы или деталей с концентраторами напряжений по результатам испытаний стандартных образцов.
2. Температура хладноломкости образцов или деталей с концентраторами напряжений может быть определена расчетным путем по экспериментально определенной характеристике прочности стали – критическому максимальному локальному растягивающему напряжению σF, температурной зависимости предела текучести и перенапряжению общей текучести.
Рецензенты:
Янукян Э.Г., д.ф.-м.н., декан инженерного факультета, Северо-Кавказский федеральный университет, филиал, г. Пятигорск;
Казуб В.Т., д.т.н., профессор, заслуженный деятель науки и образования РАЕ, зав. кафедрой физики и математики Пятигорской государственной фармацевтической академии, г. Пятигорск.
Работа поступила в редакцию 07.03.2013.
Библиографическая ссылка
Сибилёв А.В., Мишин В.М. УСТАНОВЛЕНИЕ КРИТЕРИЯ ХЛАДНОЛОМКОСТИ СТАЛЬНЫХ ОБРАЗЦОВ НА ОСНОВЕ КРИТЕРИЯ ЛОКАЛЬНОГО РАЗРУШЕНИЯ // Фундаментальные исследования. 2013. № 4-4. С. 843-847;URL: https://fundamental-research.ru/ru/article/view?id=31283 (дата обращения: 05.03.2026).



