В настоящее время производство сухих строительных смесей в нашей стране является одним из наиболее интенсивно развивающихся направлений строительной индустрии. Основными процессами технологической цепочки производства сухих строительных смесей, оказывающих существенное влияние на их эксплуатационные характеристики, является подготовка сырьевых компонентов, их дозирование и смешивание, распределение химических добавок в основной массе продукта. Однородность материала является основой требуемого качества современных строительных смесей.
Именно по этим причинам смесительный узел по праву считается наиболее ответственным участком завода по производству сухих строительных смесей. Выбор смесительного оборудования является важнейшим шагом на пути получения высококачественного продукта. В связи с чем инновационными разработками в области смесительного оборудования являются пневмосмесители. В настоящее время пневмосмесители используются для смешивания сухих строительных смесей, формовочных смесей, пищевых концентратов и фармацевтических продуктов [4, 5].
Цель исследования: разработка конструкции пневмосмесителя и методики расчёта скорости частиц в загрузочной трубе, с учётом конструктивно-технологических параметров данного агрегата.
Материалы и методы исследования
Для опытных лабораторных испытаний использовалась двухкомпонентная смесь ‒ песок и цемент, а энергоноситель – сжатый воздух, подаваемый компрессором в пневмосмеситель. Расчёт скорости частиц материала проводился с использованием аналитических уравнений движения твердых частиц материала, поставляемых питателями, в воздушном потоке загрузочной трубы. При вязком движении на горизонтальном участке загрузочной трубы на частицу материала будет действовать сила межфазного взаимодействия.
Результаты исследования и их обсуждение
В Белгородском государственном технологическом университете им. В.Г. Шухова коллективом авторов разработан и создан пневмосмеситель непрерывного действия для производства сухих строительных смесей [4].
Изобретение направлено на повышение эффективности перемешивания за счёт увеличения скорости подачи смешиваемых компонентов в зону гомогенизации, обеспечение непрерывного производства сухих строительных смесей с гарантированным качеством.
Используя определённые допущения, рассмотрим движение твердых частиц материала, поставляемых питателями, в воздушном потоке загрузочной трубы. При вязком движении на горизонтальном участке загрузочной трубы на частицу материала будет действовать сила межфазного взаимодействия, значение которой будет определяться следующим выражением:
![]() (1)
(1)
где Cо – коэффициент сопротивления частицы; ρ – плотность воздуха (кг/м3); S – миделево сечение частицы (м2); U – скорость движения частицы материала в разгонной трубе (м/с).
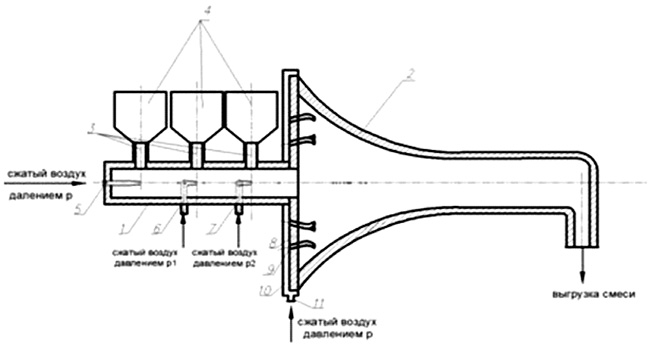
Пневмосмеситель: 1 – труба подающая; 2 – корпус; 3 – патрубок ввода; 4 – бункер; 5, 6, 7 – сопла дополнительные; 8 – торец; 9 – сопла; 10 – крышка; 11– патрубок подвода
На основании соотношения (1) уравнение движения частицы материала массой «mi» можно записать как
![]() (2)
(2)
Если учесть, что масса частицы материала определяется соотношением
mi = V∙γi, (3)
где d – диаметр частицы (м); γi – плотность частицы материала применительно к «i»- компоненте; V – объём частицы материала (м3), который можно привести к следующему виду:
![]() (4)
(4)
С учетом (4) формула (3) принимает вид:
![]() (5)
(5)
Подстановка (5) в уравнение (2) приводит к следующему результату:
![]() (6)
(6)
Сложность при нахождении решения нелинейного дифференциального уравнения (2.6) заключается в определении зависимости коэффициента сопротивления частицы материала от скоростного режима движения частицы, а именно
Co = f(Re); (7)
здесь Re – число Рейнольдса, которое равно
![]() (8)
(8)
при U > ϑ число ![]() где v – коэффициент кинематической вязкости (м2/с).
где v – коэффициент кинематической вязкости (м2/с).
Согласно литературным источникам [1–3], наиболее точно зависимость коэффициента лобового сопротивления частиц материала от числа Re в диапазоне 1 < Re < 103 определяется формулой Клячко:
![]() (9)
(9)
С учётом (8) формула Клячко принимает следующий вид:
![]() . (10)
. (10)
Подстановка выражений (10) в уравнение (6) приводит к следующему результату:
![]() (11)
(11)
где введены следующие обозначения:
![]() (12)
(12)
и
![]() (13)
(13)
В уравнении (11) от переменной дифференцирования «t» перейдёт к безразмерной переменной t согласно соотношению:
![]() (14)
(14)
С учетом выражения (14) уравнение (11) принимает вид:
![]() (15)
(15)
где
![]() (16)
(16)
а W = (U – ϑ). (17)
В соотношении (15) согласно выражению (17) W представляет собой скорость движения частицы материала относительно скорости энергоносителя (воздуха) и характеризует отставание частицы материала от энергоносителя.
Если уравнение (15) переписать в следующем виде:
![]() (18)
(18)
тогда дифференциальное уравнении (18) представляет собой хорошо известное уравнение Бернули [2, 6], которое с помощью замены
![]() (19)
(19)
позволяет нелинейное уравнение (18) относительно функции W преобразовать в линейное уравнение относительно функции z(τ):
![]() (20)
(20)
Легко убедиться, что решение уравнения (20) имеет следующий вид:
![]() (21)
(21)
где zo – постоянная интегрирования.
Постоянную интегрирования, входящую в выражение (21), можно найти, исходя из следующего граничного условия:
при t = τ = 0; ϑ = 0; U = U0 = const, (22)
где U0 – начальное значение скорости энергоносителя, которое считается постоянной величиной вдоль поперечного сечения загрузочной трубы. Начальное значение скорости энергоносителя (воздуха) можно определить из соотношения, определяющего скорость истечения газа из отверстия в тонкой стенке [5]:
![]() (23)
(23)
где φ0 – коэффициент скорости, равный φ0 = 0,668; P1 – давление в сопле (Па); P2 – наружное давление (Па); ρ0 – плотность (кг/м3) воздуха, которую можно найти на основании закона, связывающего давление и температуру при изотермическом процессе:
![]() (24)
(24)
где R – универсальная газовая постоянная.
С учетом (19) и (17) выражение (21) приобретает следующий вид:
![]() (25)
(25)
Постоянную zo можно найти, исходя из выражения (22). Подстановка (22) в (25) приводит к следующему результату:
![]() (26)
(26)
На основании (26) находим, что
![]() (27)
(27)
Подстановка (27) в (25) позволяет получить соотношение следующего вида:
![]() (28)
(28)
Будем исходить из предположения, что на всём пути загрузочной трубы скорость сжатого воздуха остаётся постоянной величиной, равной U0, тогда на основании сказанного выражение (28) принимает вид:
![]() (29)
(29)
Введём величину τ0 согласно соотношению:
![]() (30)
(30)
Легко убедиться, что введённая величина τ0 имеет размерность времени, которую назовём временем релаксации.
Введём величину ϑ0 согласно соотношению:
![]() (31)
(31)
Величина (31) имеет размерность скорости. Поэтому данную величину уместно называть скоростью торможения частицы материала за счёт кинетической вязкости среды и размера частицы.
С учётом соотношений (14), (30) и (31) выражение (29) можно представить в следующем виде:
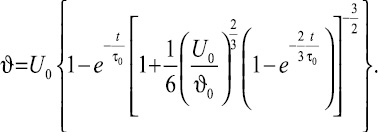 (32)
(32)
Рассмотрим промежуток времени значительно меньше времени релаксации (30), т.е. промежуток, для которого выполняется соотношение
t << τ0 t. (33)
Для рассматриваемого интервала времени, удовлетворяющего условию (33) с точностью до величин первого порядка малости, можно заключить, что
![]() (34)
(34)
и
![]() (35)
(35)
Подстановка (34) и (35) в выражение (32) с точностью до величины первого порядка малости и приводит к соотношению:
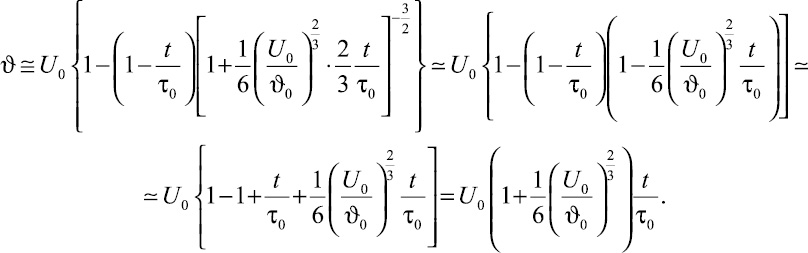 (36)
(36)
Таким образом, для промежутков времени (33) изменение скорости движения частиц материала в загрузочной трубе на основании полученного соотношения (36) происходит по линейному закону.
Для определения времени нахождения частиц материала в загрузочной трубе вычислим величину ускорения частиц материала. Вычислим производную от (36), по времени, получим следующий результат:
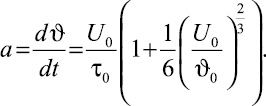 (37)
(37)
Согласно соотношению (37), частицы материала внутри загрузочной трубы для интервала времени (33) движутся с постоянным ускорением. Поэтому соотношение, связывающее пройденный путь и время движения частицы, имеет вид:
![]() (38)
(38)
здесь l – длина участка загрузочной трубы; Δt – интервал времени, в течение которого частица материала движется по загрузочной трубе в камеру смешивания.
На основании (38) находим, что время нахождения частицы материала в загрузочной трубе будет определяться соотношением
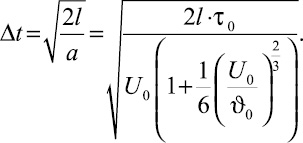 (39)
(39)
Поэтому на входе в камеру смешивания частица материала с диаметром d и кинематической вязкостью среды будет иметь следующее значение скорости:
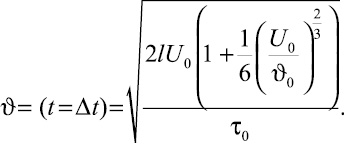 (40)
(40)
Заключение
Результаты проведенных исследований использования пневмосмесителя непрерывного действия для производства сухих строительных смесей, учитывая полученное значение скорости входа частицы материала в камеру смешения согласно (40), которое зависит как от конструктивного параметра l – длины загрузочной трубы, так и от технологических параметров: коэффициента кинематической вязкости v, диаметра частицы d, плотности материала γ, плотности энергоносителя ρ, а также начальной скорости энергоносителя U0, позволяют эффективно использовать данную установку в производстве и рассчитывать скорости движения частиц материала по загрузочной трубе данного устройства.
Рецензенты:
Шарапов Р.Р., д.т.н, профессор, зав. кафедрой подъемно-транспортных и дорожных машин, БГТУ им. В.Г. Шухова, г. Белгород;
Лозовая С.Ю., д.т.н., профессор кафедры механического оборудования, БГТУ им. В.Г. Шухова, г. Белгород.
Работа поступила в редакцию 19.02.2013
Библиографическая ссылка
Орехова Т.Н., Уваров В.А. ОПРЕДЕЛЕНИЕ СКОРОСТИ ЧАСТИЦ МАТЕРИАЛА ПНЕВМОСМЕСИТЕЛЯ СУХИХ СТРОИТЕЛЬНЫХ СМЕСЕЙ // Фундаментальные исследования. 2013. № 4-3. С. 592-596;URL: https://fundamental-research.ru/ru/article/view?id=31238 (дата обращения: 05.01.2026).



