В данной статье на основе анализа корреляционных зависимостей проводится анализ возможности прогнозирования рядов акций крупных российский компаний и банков, а именно: АвтоВАЗ, Аэрофлот, Башнефть, ВТБ, Камаз, Лукойл, МТС, Роснефть, РусГидро, Сбербанк, Сургутнефтегаз.
1. Постановка задачи и порядок анализа
В целях работы было выбрано 11 компаний (АвтоВАЗ, Аэрофлот, Башнефть, ВТБ, Камаз, Лукойл, МТС, Роснефть, РусГидро, Сбербанк, Сургутнефтегаз), цены акций которых были взяты за период 8 месяцев. Необходимо проанализировать, как влияет высокая корреляционная зависимость между ценами акций попарно на критерий выбора данных для нейросетевого прогнозирования.
В качестве данных берутся ряды цен акций представленных компаний за период с 1 января 2012 года по 22 августа 2012 года.
Для проведения анализа необходимо осуществить следующие шаги:
1. Вычисление коэффициента корреляции между каждым из рядов.
2. Выбор пар тех рядов, между которыми коэффициент корреляции r > 0,9.
3. Использование одного ряда такой пары в качестве входного вектора в нейронную сеть, другого ряда – в качестве целевого вектора.
4. Для обучения данные оптимизируются генетическим алгоритмом.
5. Обучение нейронной сети.
6. Анализ выходных данных.
7. Проверка утверждений.
2. Результаты эксперимента
Из проведенного анализа корреляционных зависимостей видно, что существует ряд пар акций, имеющих коэффициент корреляции больше 0,9. Данные пары представлены в табл. 1.
Таблица 1
Пары акций с высокой корреляцией
|
Пара акций |
Коэффициент корреляции, Cor |
|
АвтоВаз – ВТБ |
0,93 |
|
АвтоВаз – РусГидро |
0,94 |
|
ВТБ – РусГидро |
0,97 |
|
Сбербанк – Сбербанк (привил.) |
0,95 |
|
Сбербанк – Сургутнефтегаз |
0,93 |
Цены акции данных пар используются для входных данных в нейронную сеть.
Для анализа используется нейронная сеть архитектуры MLP – многослойный персептрон вида Generalized One Layer. Нейросетевой анализ проводится в среде Peltarion Synapse.
Далее, поочередно проводится нейросетевой анализ для выбранных пар.
Для анализа пары «АвтоВАЗ» – «ВТБ» обучается нейронная сеть, и на вход подаются цены акций «АвтоВАЗ», а в качестве целевых значений цены акций «ВТБ». На верхнем графике рис. 1,a наглядно представлены результаты обучения нейронной сети. Кривая сиреневого цвета – это выходные данные сети (Output), а кривая черного цвета – это целевые значения (Desired), то есть цены акций «ВТБ». На нижнем графике рис. 1,a представлены результаты этапа проверки выходных данных на выборочных значениях, подаваемых в обученную нейронную сеть. Значения в цифрах представлены в табл. 2.
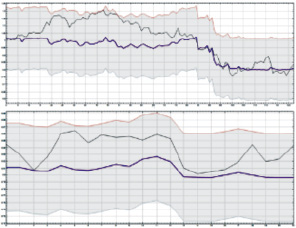
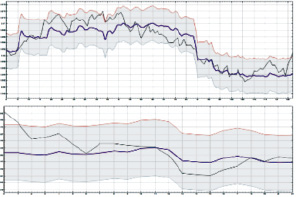
Рис. 1. Нейросетевой анализ пар: а – «АвтоВАЗ» – «ВТБ»; б – «АвтоВАЗ» – «РусГидро»
Средняя ошибка обучения нейронной сети Е = –0,0002341, среднее значение выходных данных OUTср = 0,054363.
Аналогично для всех других пар акций с высокой корреляцией проводится нейросетевой анализ. Только в качестве входных значений подаются цены акций соответствующей пары.
Для пары акций «АвтоВАЗ» – «РусГидро» обученная модель представлена на верхнем графике рис. 1,б. Результаты проверки представлены на нижнем графике того же рисунка. Значения в цифрах представлены в табл. 3.
Таблица 2
|
Desired (ВТБ) |
Output |
Ошибка |
|
0,06026 |
0,054655 |
–0,00561 |
|
0,0586 |
0,05466 |
–0,00394 |
|
0,05625 |
0,054486 |
–0,00176 |
|
0,0565 |
0,054436 |
–0,00206 |
|
0,05713 |
0,05476 |
–0,00237 |
|
0,0555 |
0,054527 |
–0,00097 |
|
0,05425 |
0,054488 |
0,000238 |
|
0,0556 |
0,054632 |
–0,00097 |
|
0,0556 |
0,054814 |
–0,00079 |
|
0,05536 |
0,054716 |
–0,00064 |
|
0,05519 |
0,055046 |
–0,00014 |
|
0,05512 |
0,055149 |
2,86E–05 |
|
0,05395 |
0,054935 |
0,000985 |
|
0,0514 |
0,053827 |
0,002427 |
|
0,05121 |
0,053709 |
0,002499 |
|
0,05107 |
0,053642 |
0,002572 |
|
0,05185 |
0,054084 |
0,002234 |
|
0,0524 |
0,054328 |
0,001928 |
|
0,05361 |
0,054085 |
0,000475 |
|
0,05303 |
0,053718 |
0,000688 |
|
0,05375 |
0,053632 |
–0,00012 |
|
0,0535 |
0,053649 |
0,000149 |
Таблица 3
|
Desired (РусГидро) |
Output |
Ошибка |
|
0,8445 |
0,811247 |
–0,03325 |
|
0,8297 |
0,811394 |
–0,01831 |
|
0,8076 |
0,807081 |
–0,00052 |
|
0,826 |
0,805976 |
–0,02002 |
|
0,8603 |
0,81414 |
–0,04616 |
|
0,865 |
0,808025 |
–0,05698 |
|
0,847 |
0,80713 |
–0,03987 |
|
0,8584 |
0,810641 |
–0,04776 |
|
0,8545 |
0,815731 |
–0,03877 |
|
0,856 |
0,812904 |
–0,0431 |
|
0,8508 |
0,823174 |
–0,02763 |
|
0,8592 |
0,826778 |
–0,03242 |
|
0,8527 |
0,819486 |
–0,03321 |
|
0,8106 |
0,797129 |
–0,01347 |
|
0,8015 |
0,796481 |
–0,00502 |
|
0,805 |
0,796277 |
–0,00872 |
|
0,8081 |
0,799769 |
–0,00833 |
|
0,8192 |
0,803747 |
–0,01545 |
|
0,8443 |
0,799782 |
–0,04452 |
|
0,8197 |
0,79652 |
–0,02318 |
|
0,8234 |
0,796256 |
–0,02714 |
|
0,8432 |
0,796293 |
–0,04691 |
Средняя ошибка Е = –0,02867, среднее значение выходных данных OUTср = 0,807089.
Для «ВТБ» – «РусГидро» обученная модель представлена на верхнем графике рис. 2,а. Результаты проверки представлены на нижнем графике рис. 2,а. Значения в цифрах представлены в табл. 4.
Средняя ошибка Е = –0,0671023, среднее значение выходных данных OUTср = 0,768657.
Для пары акций «Сбербанк» – «Сбербанк (привил.)» обученная модель продемонстрирована на верхнем графике рис. 2,б.
Результаты проверки представлены на нижнем графике рис. 2,б. Значения в цифрах представлены в табл. 5.
Средняя ошибка Е = 2,2788367, среднее значение выходных данных OUTср = 66,93884.
Для пары акций «Сбербанк» – «Сургутнефтегаз» обученная модель представлена на верхнем графике рис. 3. Результаты проверки представлены на нижнем графике рис. 3. Значения в цифрах представлены в табл. 6.
Средняя ошибка Е = 0,3428499, среднее значение выходных данных OUTср = 27,50153.
Анализ выходных данных проводится путем сравнения ошибок, получаемых в результате разницы выходных значений и значений желаемых (фактических). Среднее значение ошибок представлено в процентном соотношении относительно среднего значения выходных значений. Это необходимо для сравнения ошибок разных цен акции в одной процентной шкале. Проверка проводится заранее известных цен акций той или иной компании, и значений, выдаваемых нейронной сетью, которая обучена на ценах акций в предыдущие моменты времени.
Результаты сравнительного анализа продемонстрированы в табл. 7, из которой видно, что ошибка той или иной пары акции очень мала и в среднем не больше 10 % относительно выходных данных.
Проведен анализ корреляционных зависимостей между рядами цен акции. Пары с высокой корреляцией использовались в качестве входных данных для нейронной сети. Тем самым имеет место подтверждение того, что высокий коэффициент корреляции может использоваться в качестве критерия для нейросетевого прогнозирования.
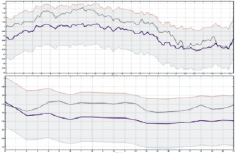
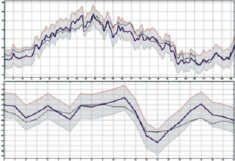
Рис. 2. Нейросетевой анализ пар: а – ВТБ» – «РусГидро»; б – «Сбербанк» – «Сбербанк (привил.)»
Таблица 4
|
Desired (РусГидро) |
Output |
Ошибка |
|
0,8445 |
0,860889 |
0,016389 |
|
0,8297 |
0,825549 |
–0,00415 |
|
0,8076 |
0,783288 |
–0,02431 |
|
0,826 |
0,787001 |
–0,039 |
|
0,8603 |
0,797225 |
–0,06307 |
|
0,865 |
0,773255 |
–0,09175 |
|
0,847 |
0,759667 |
–0,08733 |
|
0,8584 |
0,774502 |
–0,0839 |
|
0,8545 |
0,774502 |
–0,08 |
|
0,856 |
0,771553 |
–0,08445 |
|
0,8508 |
0,769552 |
–0,08125 |
|
0,8592 |
0,768749 |
–0,09045 |
|
0,8527 |
0,756877 |
–0,09582 |
|
0,8106 |
0,738092 |
–0,07251 |
|
0,8015 |
0,736958 |
–0,06454 |
|
0,805 |
0,736141 |
–0,06886 |
|
0,8081 |
0,740899 |
–0,0672 |
|
0,8192 |
0,744584 |
–0,07462 |
|
0,8443 |
0,753896 |
–0,0904 |
|
0,8197 |
0,749202 |
–0,0705 |
|
0,8234 |
0,755101 |
–0,0683 |
|
0,8432 |
0,752969 |
–0,09023 |
Таблица 5
|
Desired (Сбербанк (привил.)) |
Output |
Ошибка |
|
65,86 |
68,61142 |
2,751417 |
|
65,2 |
68,382 |
3,182003 |
|
63,61 |
66,23905 |
2,629047 |
|
64,21 |
67,24701 |
3,037013 |
|
66 |
68,48389 |
2,483892 |
|
65,71 |
67,23455 |
1,524548 |
|
65,3 |
65,9024 |
0,602398 |
|
66,94 |
68,45841 |
1,518408 |
|
66,97 |
68,29296 |
1,322955 |
|
67,16 |
68,76466 |
1,60466 |
|
66,63 |
69,25107 |
2,621068 |
|
66,63 |
69,95625 |
3,326248 |
|
65,25 |
67,37187 |
2,12187 |
|
61,75 |
62,70401 |
0,95401 |
|
61,66 |
61,28077 |
-0,37923 |
|
61,91 |
63,62189 |
1,711886 |
|
62,82 |
65,34739 |
2,527388 |
|
63,86 |
67,61007 |
3,75007 |
|
64,43 |
68,79022 |
4,360221 |
|
63,3 |
66,88713 |
3,587128 |
|
63,9 |
66,46983 |
2,569827 |
|
63,42 |
65,74758 |
2,327577 |
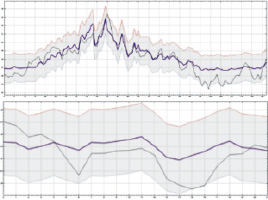
Рис. 3. Нейросетевой анализ пары «Сбербанк» – «Сургутнефтегаз»
Таблица 6
|
Desired (Сургутфетегаз) |
Output |
Ошибка |
|
28,507 |
27,69271 |
–0,81429 |
|
28,372 |
27,66029 |
–0,71171 |
|
27,895 |
27,39594 |
–0,49906 |
|
28 |
27,51238 |
–0,48762 |
|
27,714 |
27,67458 |
–0,03942 |
|
27,027 |
27,51086 |
0,483859 |
|
26,341 |
27,3597 |
1,018704 |
|
27,221 |
27,67099 |
0,449986 |
|
27,227 |
27,64795 |
0,42095 |
|
27,331 |
27,71489 |
0,383893 |
|
27,35 |
27,78824 |
0,438237 |
|
27,43 |
27,90328 |
0,473283 |
|
27,167 |
27,52771 |
0,360713 |
|
26,194 |
27,06494 |
0,870942 |
|
25,93 |
26,95433 |
1,024327 |
|
25,769 |
27,14187 |
1,372874 |
|
25,919 |
27,30252 |
1,383516 |
|
26,69 |
27,55758 |
0,867578 |
|
27,173 |
27,71863 |
0,545634 |
|
27,207 |
27,46935 |
0,26235 |
|
27,577 |
27,42151 |
–0,15549 |
|
27,45 |
27,34344 |
–0,10656 |
Таблица 7
|
Акции |
Средняя ошибка |
Среднее выходное значение |
Процент |
|
АвтоВаз – ВТБ |
–0,0002341 |
0,054363 |
–0,4307 |
|
АвтоВаз – РусГидро |
–0,02867 |
0,807089 |
–3,55227 |
|
ВТБ – РусГидро |
–0,0671023 |
0,768657 |
–8,72981 |
|
Сбербанк – Сбербанк (привил.) |
2,2788367 |
66,93884 |
3,404357 |
|
Сбербанк – Сургутнефтегаз |
0,3428499 |
27,50153 |
1,246657 |
Рецензенты:
Семенчин Е.А., д.ф.-м.н., профессор, зав. каф. высшей алгебры и геометрии Кубанского государственного университета, г. Краснодар;
Халафян А.А., д.ф.-м.н., профессор кафедры прикладной математики Кубанского государственного университета, г. Краснодар.
Работа поступила в редакцию 21.01.2013.
Библиографическая ссылка
Шахмеликян Т.А., Кесиян Г.А., Уртенов М.Х. ИСПОЛЬЗОВАНИЕ КОРРЕЛЯЦИОННОГО АНАЛИЗА ПРИ НЕЙРОСЕТЕВОМ ПРОГНОЗИРОВАНИИ КУРСОВ АКЦИЙ // Фундаментальные исследования. 2013. № 4-1. С. 224-228;URL: https://fundamental-research.ru/ru/article/view?id=31133 (дата обращения: 12.03.2026).



