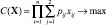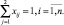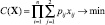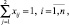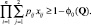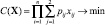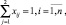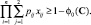В работах [1–3] показано, что современные субъекты общественного производства в задачах адаптивного управления следует рассматривать как системы производства−потребления. Их принципиальной особенностью является представление потребителей как одной из ключевых составляющих системы. Развитая теория таких систем – теория производства−потребления [3] оперирует элементами качества жизни (КЖ) потребителя, «переносимыми» продукцией, и определяет вид решения изготовителя в виде вектора Х = {xij}, j = 1, 2. Компоненты вектора принимают значение 1, если соответствующий элемент (элемент КЖ – j = 1 или его «отсутствие» – j = 2) включен в профиль качества продукции, или 0 – в противоположном случае. Положения теории производства−потребления и ее интерпретация в виде цепочечных бинарных структур [4] обусловливают выбор конечного цепочечного двумерного (плоского) ориентированного графа с потоками в качестве базовой модели теории. В распространенном варианте задач поток в компонентах графа – относительный (приведенный к мощности истока) поток потребителей.
С целью определения условий адекватного применения модели рассмотрим ее особенности, раскроем потенциальные ошибки расчетов и пути их устранения.
Особенности конечного двумерного орграфа с потоками
Звено i двумерного цепочечного орграфа с потоками в соответствии с введенной в работе [4] x-ячейкой бинарной структуры имеет вид (рис. 1).
Поток вершины S (истока) при компоненте решения производителя продукции xi1 = 1 обозначен Рi1, поток вершины S при xi1 = 0 – Рi2, при этом очевидно Рi1 = Рi2. Вершина DC расщепляет поток Рi1 на два потока: Р+i1 = pi1Рi1 и РCi = (1 – pi1)Рi1 – доли потока потребителей, соответственно имеющих и не имеющих возможность приобретения продукции с i-м элементом качества. Вершина DQ расщепляет поток Рi2 на два потока: Р+i2 = pi2Рi2 и РQi = (1 – pi2)Рi2 – доли потока потребителей, соответственно удовлетворенных и не удовлетворенных качеством продукции без i-го элемента качества. Здесь pij (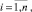 j = 1,2) – коэффициенты передачи потока звена i. Мощность (поступающий поток) вершины G (стока) равна Р+i1 при xi1 = 1 или Р+i2 при xi1 = 0. Приведенное на рис. 1 звено описывает отношение потребителя к одному конкретному решению производителя (к одному элементу КЖ). При
j = 1,2) – коэффициенты передачи потока звена i. Мощность (поступающий поток) вершины G (стока) равна Р+i1 при xi1 = 1 или Р+i2 при xi1 = 0. Приведенное на рис. 1 звено описывает отношение потребителя к одному конкретному решению производителя (к одному элементу КЖ). При 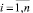 орграф будет состоять из n подобных звеньев, а число вариантов решений равно 2n.
орграф будет состоять из n подобных звеньев, а число вариантов решений равно 2n.
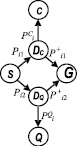
Рис. 1. Звено модели
Рассмотрим возможности введенной модели на примере моделирования услуги телефонной связи (n = 12), приведенного в работе [5]. Графовая модель этой услуги представлена на рис. 2. Здесь видна периодическая структура орграфа, в котором внутренние вершины, подобные вершине S (рис. 1), обозначены символом Ai, 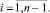 Число дуг и вершин различных структурных типов, их связь с объемом учитываемых элементов КЖ приведены в табл. 1. Любому варианту решения в отличие от сетевой модели соответствует не путь на графе, а его подграф с числом дуг, равным 50 % всех дуг и количеством вершин, равным 2(n + 1) или 2/3 всех вершин. Поиск оптимальных решений выполняется в соответствии с приведенными характеристиками орграфа по целевым функциям и ограничениям, приведенным в табл. 2. Здесь же показаны результаты расчетов по данным примера [5], модель которого показана на рис. 2. Подграф оптимального решения (задача 1, табл. 2) выделен на рис. 2 жирными дугами.
Число дуг и вершин различных структурных типов, их связь с объемом учитываемых элементов КЖ приведены в табл. 1. Любому варианту решения в отличие от сетевой модели соответствует не путь на графе, а его подграф с числом дуг, равным 50 % всех дуг и количеством вершин, равным 2(n + 1) или 2/3 всех вершин. Поиск оптимальных решений выполняется в соответствии с приведенными характеристиками орграфа по целевым функциям и ограничениям, приведенным в табл. 2. Здесь же показаны результаты расчетов по данным примера [5], модель которого показана на рис. 2. Подграф оптимального решения (задача 1, табл. 2) выделен на рис. 2 жирными дугами.
Значения целевой функции (табл. 2, задачи 2 и 3) приведены для нескольких значений величины j0, имеющей смысл максимальной доли потенциальных потребителей, не удовлетворенных соответственно качеством и ценой продукции. Задача 2 актуальна для стратегии достижения конкурентоспособности на основе роста качества продукции. Задача 3 актуальна для стратегии достижения конкурентоспособности на основе ценового подхода.
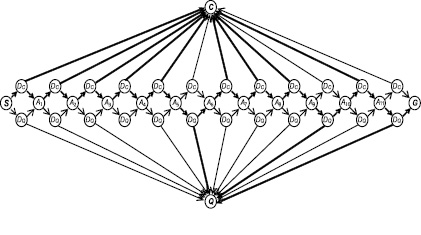
Рис. 2. Графовая модель услуги телефонной связи, рассмотренной в [5]
Таблица 1
Соотношения размерности вектора решений и параметров модели
|
Количество компонентов решения |
Количество вершин |
||||||
|
Всего |
A |
C |
D |
G |
Q |
S |
|
|
n |
3(n + 1) |
n – 1 |
1 |
2n |
1 |
1 |
1 |
|
Количество решений |
Количество дуг |
Количество дуг в решении |
|||||
|
2n |
6n |
3n |
|||||
Анализ адекватности введенного орграфа теории производства−потребления
При решении задач прогнозирования на основе конечного двумерного орграфа, в частности, задач оптимизации, указанных в табл. 2, возможны следующие противоречия:
Противоречие 1-го рода. Найдено значение целевой функции С(Х), отличающееся от действительного значения на величину больше допустимой относительной погрешности δmax.
Противоречие 2-го рода. Найден вектор решения Х = {xi1}, отличающийся от действительного оптимального решения хотя бы одним его компонентом xi1, 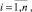 .
.
Противоречие 3-го рода. Найдено оптимальное решение Х = {xi1}, 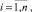 хотя при заданных ограничениях на целевую функцию С(Х) его не существует.
хотя при заданных ограничениях на целевую функцию С(Х) его не существует.
Таблица 2
Модели и примеры решения практических задач оптимизации
|
Модель и решения Задачи |
Целевая функция C(X) |
Ограничения |
Оптимальное решение X = {xi1} для примера [5] |
Значение C(X) |
|
Задача 1 − максимизация потока к вершине G |
|
|
{1,1,1,1,1,0,1,1,1,0,1,0} |
0,3400 |
|
Задача 2 − минимизация потока к вершине G до порога [1−j0(Q)] при нулевом потоке к вершине C |
|
|
{1,1,1,1,1,0,1,1,1,0,1,0} {1,1,1,1,1,0,1,1,0,0,1,1} {1,1,1,1,1,0,1,1,0,0,1,0} |
0,8464 j0(Q) = 0.2 0,7054 j0(Q) = 0.3 0,6348 j0(Q) = 0.4 |
|
Задача 3 − минимизация потока к вершине G до порога [1−j0(C)] при нулевом потоке к вершине Q |
|
|
{0,0,0,0,0,0,1,0,0,0,0,0} {1,0,0,0,0,0,0,1,1,0,1,0} {1,0,0,1,1,0,0,0,1,0,1,0} |
0,8000 j0(C) = 0.2 0,7049 j0(C) = 0.3 0,6150 j0(C) = 0.4 |
С целью определения источника противоречивости модели и формализации условий ее адекватности конкретизируем ряд понятий теории производства−потребления.
Определение 1. Элементом качества жизни человека принимаем положительное субъективно переживаемое чувство, возникающее при потреблении продукта (услуги), однозначно испытываемое и обозначенное членами социума.
Определение 2. Вид связи «потребленный продукт – чувства» определим как «один ко многим». Продукция рассматривается как физический «носитель» нескольких элементов КЖ.
Определение 3. Структурированным множеством элементов КЖ называется такое множество KS, каждому элементу которого социумом поставлено в соответствие одно определенное наименование, а каждому определенному наименованию поставлен в соответствие один элемент. Речь идет о конечном множестве элементов КЖ, сформулированных и принятых таковыми социумом.
Определение 4. Универсумом качества жизни считаем бесконечное множество KU, состоящее из структурированного конечного подмножества элементов КЖ, которые определены в настоящее время, и неструктурированного бесконечного подмножества элементов КЖ, элементы которого в настоящий момент времени неизвестны. По мере развитие социума отдельные элементы множества KU будут определены и перейдут в структурированное множество элементов КЖ KS. Приведенные определения позволяют раскрыть источник указанных потенциальных противоречий как несовпадения множеств KP, KM и KS (рис. 3).
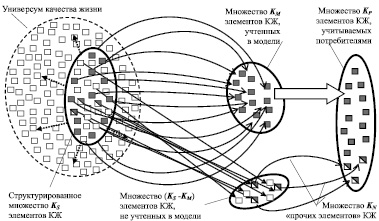
Рис. 3. Взаимосвязи множеств элементов качества жизни потребителя
С целью определения признаков указанных противоречий сформулируем лемму.
Лемма. Значение целевой функции С(Хn), найденное по конечному орграфу с потоком, всегда не меньше значения целевой функции С(Хn + 1), определенного по этому же графу, увеличенному хотя бы на одно звено, т.е. справедливо нестрогое неравенство
С(Хn) ≥ С(Хn + 1). (1)
Доказательство. Допустим случай, когда значение целевой функции С(Х), найденное по конечному орграфу с числом звеньев n, меньше значения целевой функции, определенного по этому же графу, увеличенному на одно (n + 1)-е звено. Это значит, что хотя бы один из коэффициентов передачи pij этого звена удовлетворял условию
pij > 1, 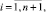 j = 1,2. (2)
j = 1,2. (2)
С другой стороны, соотношения потоков дуг, инцидентных вершинам DC и DQ (рис. 1), в соответствии с правилами вершин графа с направленными потоками [6] имеют вид:
Рi1 = РCi+Р+i1, Рi2 = РQi+Р+i2. (3)
Из (3) следует, что истинны выражения (рис. 1):
pi1 = Р+i1/Рi1 = Р+i1/(РCi+Р+i1) ≤ 1,
pi2 = Р+i2/Рi2 = Р+i2/(РQi+Р+i2) ≤ 1, (4)
что противоречит допущенному условию (2), следовательно, указанный случай невозможен. Лемма доказана.
Из леммы следует ряд выводов. Во-первых, отсутствие в орграфе хотя бы одного звена может привести к решению Х, отличающемуся от противоположного случая. Во-вторых, указанная ошибка может привести к изменению значения целевой функции С(Х), причем только в большую сторону. Кроме того, из леммы следует, что эта ошибка может быть устранена введением в орграф специального звена – звена ошибки.
Определение 5. Звеном ошибки примем звено орграфа, относящееся к множеству элементов КЖ «прочие» и характеризующееся единственным решением xe1 = 0 (xe2 = 1).
Наличие звена ошибок (E-звена) отражает факт отсутствия в профиле продукции не какого-либо конкретного элемента КЖ (что в общем характерно для ранее рассмотренных и приведенных на рис. 1 звеньев), а множества неучтенных в модели прочих элементов КЖ – KN. Множество KN есть та часть множества KS, на которой не были определены параметры модели pij, но которая принимается во внимание частью потребителей при принятии решений об уровне качества продукции. Эта часть потребителей обусловит отличие рассчитанного без ее учета оптимального решения от фактического. На основе определения 5 фрагмент орграфа со звеном ошибки принимает вид (рис. 4). Здесь штриховыми линиями показаны компоненты орграфа, к которым подключаются четыре порта звена ошибок. В отличие от ранее введенных звеньев (см. рис. 1), E-звено описывает преобразование потока потребителей в два непересекающихся множества: множество потребителей, неудовлетворенных профилем качества продукции из-за отсутствия прочих элементов KN – поток (1 – pE2)j(Ai), и множество потребителей, которым это отсутствие неважно (поток pE2j(Ai)).
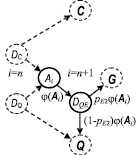
Рис. 4. Звено ошибки
Критерии непротиворечивости и условия её достижения
Модель теории производства-потребления в виде конечного двумерного орграфа будет непротиворечивой, если
[С(Хn) – С(ХnE)]/С(Хn) ≤ δmax, (5)
M(Хn, ХnE[n]) = 0. (6)
Здесь С(Хn) и Хn – соответственно значение целевой функции и ее аргумент, определенные по орграфу без звена ошибки, С(ХnE) и ХnE – аналогичные результаты расчетов, выполненных с учетом звена ошибок, δmax – заданный допуск на величину целевой функции, M(Хn,ХnE[n]) – расстояние между векторами Хn и ХnE, в котором учтены первые n элементов). Поскольку элементы векторов принимают только дискретные значения 0 и 1, то для их представления в пространстве состояний правомерно использовать пространство Хемминга. Критерий (6) имеет смысл отсутствия искажения хотя бы в одном компоненте решения Хn = {xi}, , а расстояние (метрика Хемминга) между векторами Хn и ХnE есть результат сложения по модулю 2 последовательности компонентов решений Хn = {xi} и ХnE[n]:
M(Хn, ХnE[n]) = Хn ⊕ ХnE[n]. (7)
Теорема. Для того чтобы конечный двумерный орграф с потоками был непротиворечивым теории производства−потребления, необходимо и достаточно, чтобы коэффициент передачи звена ошибок pE2 удовлетворял условиям:
pE2 ≥ (1 – δmax)
и
pE2 ≥ (1 – j0)/Cmin(Хn,j0). (8)
Здесь Cmin(Хn,j0) – значение целевой функции, найденное по модели без звена ошибок при решении задачи минимизации потока к вершине G до порогового значения (1 – j0(Q/C)) при нулевом потоке к вершине C/Q.
Доказательство. Предположим, имеет место случай, когда pE2 < (1 – δmax).
В соответствии с леммой значение С(Хn) будет больше значения С(ХnE), а в соответствии с выражениями для целевой функции (табл. 1), величина этой разности будет равна
С(Хn) – С(ХnE) = С(Хn)(1 – pE2). (9)
В соответствии с допущенным случаем из (9) следует
С(Хn) – С(ХnE) > δmax С(Хn), (10)
т.е. критерий непротиворечивости (5) нарушен и, следовательно, рассматриваемый случай (pE2 < 1 – δmax) невозможен.
Предположим, имеет место другой случай, когда
pE2 < (1– j0)/Сmin(Хn,j0). (11)
При решении задачи минимизации потоков в одном из стоков до заданного уровня (задачи 2 и 3, табл. ) без учета звена ошибки получим решение Хn, которое будет удовлетворять условию
0 ≤ Сmin(Хn,j0)−(1−j0) < p + (−)kjСmin(Хn,j0), (12)
где 0 ≤ pkj+(−) ≤ 1 коэффициент передачи потока любого звена графовой модели, относящегося в согласно решению Хn к элементам КЖ, соответственно включенным (задача 2) или не включенным (задача 3) в профиль качества продукции. Условие (12) выполняется во всех случаях, когда задачи 2 и 3 имеют решения при заданных ограничениях:
Сmin(Хn,j0) → min;
Сmin(Хn,j0) ≥ (1 – j0). (13)
В соответствии леммой добавление к орграфу E-звена с коэффициентом передачи pE2 приведет к уменьшению значения целевой функции Сmin(Хn,j0) в выражении (12) до величины, равной pE2Сmin(ХnE,j0). Тогда разность в (12), определенная для вектора ХnE, с учетом допущенного условия (11) будет отрицательной, что противоречит его левой части. Однако это противоречие устранимо, если найдется вектор ХnE*, для которого Сmin(ХnE*[n],j0) – (1 – j0) ≥ 0. Такой вектор ХnE* имеет место быть в том случае, когда
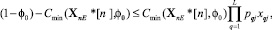 (14)
(14)
где xqj, 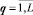 для задачи 2 (j = 1) и для задачи 3 (j = 2) – ставшие единичными элементы вектора ХnE*[n], соответствующие нулевым элементам вектора Хn; pqj – коэффициенты передачи звеньев измененных элементов xqj.
для задачи 2 (j = 1) и для задачи 3 (j = 2) – ставшие единичными элементы вектора ХnE*[n], соответствующие нулевым элементам вектора Хn; pqj – коэффициенты передачи звеньев измененных элементов xqj.
Тогда метрика Хемминга для векторов Хn и ХnE*[n], равная количеству несовпадающих значений компонентов векторов, будет больше нуля. Таким образом, существование случая (11) требует выполнение условия (14) и изменения вектора Хn на вектор ХnE*[n], однако при этом M(Хn, ХnE*[n]) ≠ 0, что противоречит критерию (6). Следовательно, рассматриваемый случай (11) невозможен. Теорема доказана.
Таким образом, в соответствии с теоремой, если pE2 < 1 – j0(Q/C) или pE2 < 1 – δmax, то орграф не удовлетворяет критерию непротиворечивости. В этом случае в орграф следует включить звено ошибки, тогда расчет даст неискаженное значение потока потребителей и соответствующий профиль качества продукции или отсутствие решения. Однако этот вариант коррекции модели не дает проектировщику и производителю информацию о направлении совершенствования продукции с целью увеличения ее востребованности. Для получения такой информации следует раскрыть множество элементов KN, относящихся к E-звену, вычленить из него элементы (элемент) КЖ, каждому из которых будет поставлено в соответствие новое звено орграфа. Тогда коэффициент передачи pE2 «сокращенного» E-звена в соответствии с леммой увеличится, что позволит выполнить условие (8) непротиворечивости модели (новый орграф будет адекватно описывать предпочтения потребителей продукции).
Применение выражений (5)–(14) для рассматриваемого примера (рис. 2) при величине pE2 = 0,95 и δmax = 4 % дает, в частности, следующие результаты:
1. В задаче 1 (табл. 2) значение целевой функции изменилось при прежнем векторе Х = {1,1,1,1,1,0,1,1,1,0,1,0} и стало равным С*(Х) = 0,323. Устранено противоречие 1-го рода.
2. В задаче 2: для вариации j0(Q) = 0,2: изменилось значение C*(Х) = 0,8041 при прежнем векторе X = {1,1,1,1,1,0,1,1,1,0,1,0}. Устранено противоречие 1-го рода; для вариации j0(Q) = 0,3: изменился вектор оптимального решения Х* = {1,1,1,1,1,1,1,1,0,0,1,1}, величина целевой функции осталась прежней C(Х*) = 0,7054. Устранено противоречие 2-го рода; для вариации j0(Q) = 0,4: изменилось значение C*(Х) = 0,6031 при прежнем векторе оптимального решения X = {1,1,1,1,1,0,1,1,0,0,1,0}. Устранено противоречие 1-го рода.
3. Применение модели в задаче, аналогичной задаче 2, при величинах pE2 = 0,93 и j0(Q) = 0,05 (случай отсутствует в табл. 2) дает следующие результаты: оптимальное решение, полученное по модели без звена ошибок, Х = {1,1,1,1,1,0,1,1,1,1,1,1} и значение целевой функции С(Х) = 0,9500; расчет по модели со звеном ошибки показывает, что в действительности оптимального решения при заданных ограничениях не существует. Введение звена ошибки позволило исключить противоречие 3-го рода.
Заключение
Раскрыты особенности конечного плоского ориентированного графа с потоками как математической модели теории производства−потребления продукции в открытых социально-экономических системах. Дана классификация возможных ошибок моделирования, поиска оптимальных решений и сформулированы условия непротиворечивости графовой модели. Предложены практически реализуемые алгоритмы оперативной (укрупненной) и уточненной коррекции введенной модели в случае ее противоречивости решаемым задачам проектирования и производства конкурентоспособной продукции.
Рецензенты:
Корнилов Д.А. д.э.н., профессор кафедры экономики и управления НГТУ им. Р.Е. Алексеева, г. Нижний Новгород;
Моругин С.Л., д.т.н., профессор, зав. кафедрой компьютерных технологий в проектировании и производстве, НГТУ им. Р.Е. Алексеева, г. Нижний Новгород.
Работа поступила в редакцию 11.01.2013.
Библиографическая ссылка
Ивлев М.А. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ПРОИЗВОДСТВА−ПОТРЕБЛЕНИЯ: ХАРАКТЕРИСТИКА И УСЛОВИЯ НЕПРОТИВОРЕЧИВОСТИ ГРАФОВЫХ МОДЕЛЕЙ // Фундаментальные исследования. 2013. № 1-3. С. 707-713;URL: https://fundamental-research.ru/ru/article/view?id=31014 (дата обращения: 02.03.2026).