Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Брянская Ю.В. 1 Байков В.Н. 1 Волынов М.А. 2

---

1 ФГБОУ ВПО «Московский государственный строительный университет»

2 ГНУ «Всероссийский научно-исследовательский институт гидротехники и мелиорации им. А.Н. Костякова»

В статье производится сравнение выражений для дефицита скорости в трубах и каналах, полученных на основе логарифмического распределения скоростей и профиля скорости степенного вида. Анализируется зависимость показателя степени профиля скорости от коэффициента гидравлического сопротивления. Показано, что рассчитанные дефициты скорости совпадают лишь при малых значениях коэффициента гидравлического сопротивления. Получена зависимость для показателя степени профиля скорости, обеспечивающая совпадение дефицитов в широком диапазоне изменения коэффициента гидравлического сопротивления. На основе дефицита средней скорости для потоков в трубах и каналах получен комплекс, включающий параметр Кармана, показатель степени профиля скорости и коэффициент гидравлического сопротивления, обладающий свойством инвариантности, которое подтверждено экспериментальными данными.

Статья в формате PDF

955 KB

турбулентное течение

профиль скорости

дефицит скорости

гидравлический инвариант

коэффициент гидравлического сопротивления

1. Шлихтинг Г. Теория пограничного слоя. – М.: Наука, 1969. – 742 с.

2. Альтшуль А.Д. Гидравлические сопротивления. – М.: Недра, 1982. – 222 с.

3. Зегжда А.П. Гидравлические потери на трение в каналах и трубопроводах. – М-Л.: Госстройиздат, 1957. – 278 с.

4. Nunner W. Warmeubergang Foorschungsheft. – 1956. – № 455. – Р. 5–39.

5. Брянская Ю.В., Байков В.Н., Волынов М.А. Распределение скоростей и гидравлическое сопротивление при течении в трубах, каналах и речных руслах // Гидротехническое строительство. – 2011. – № 3. – С. 36–39.

6. Брянская Ю.В. Течение в пристеночном слое и за его пределами (в трубе, канале и пограничном слое) // Вестник МГСУ. – 2010. – № 4, Т. 2. – С. 60–66.

7. Никурадзе И. Закономерности турбулентного движения в гладких трубах // Проблемы турбулентности. – М-Л.: Изд-во ОНТИ НКТП, 1936. – с. 75–150.

8. Богомолов А.И., Боровков В.С., Майрановский Ф.Г. Высокоскоростные потоки со свободной поверхностью. – М.: Стройиздат, 1979. – 343 с.

Как известно, универсальной формой распределения скоростей в турбулентных водных потоках, одинаковой как для гладких, так и для шероховатых граничных поверхностей, является дефицит местной скорости [1]:

– для потока в канале

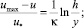(1)

– для потока в трубе

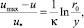(2)

где h и r0 – соответственно глубина плоского потока и радиус трубы; k – параметр Кармана.

Использование логарифмического распределения скоростей для потоков в канале и в трубе позволяет определить дефицит средней скорости:

– для потока в канале

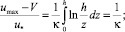(3)

– для потока в трубе

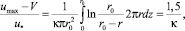(4)

где r – переменное радиальное расстояние от оси трубы; V – средняя расходная скорость.

Величины 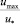и 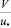являются функциями коэффициента сопротивления λ [2]. Опытами различных исследователей доказано, что коэффициент сопротивления оказывается идентичным для потоков с различной формой поперечного сечения, если в качестве геометрической характеристики сечения потока принимать гидравлический радиус 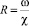(где ω – площадь сечения, χ – смоченный периметр). В условиях идентичности закономерностей сопротивления для течения в трубе и в широком открытом потоке, которая подтверждена, в частности, опытами А.П. Зегжда [3], оказывается необъяснимым факт существенного различного дефицита средней скорости для этих потоков. Для дальнейшего анализа используем профиль скорости степенного вида:

– для потока в канале

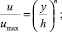(5)

– для потока в трубе

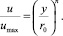(6)

Профили (5) и (6) обладают свойствами универсального распределения скоростей в каналах и трубах, если величина n адекватно определяется в виде функции коэффициента гидравлического сопротивления λ. Так, А.Д. Альтшулем и В. Нуннером [2, 4] на основе анализа экспериментальных измерений в трубах было найдено, что

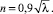(7)

С учетом (5) и (6) запишем дефицит местной скорости в следующем виде:

– для потока в канале

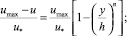(8)

– аналогично для потока в трубе

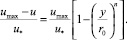(9)

Величину 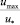заменим следующим выражением 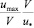, в котором 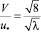, и отношение 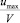выражается с учетом (5) и (6) в следующем виде для потоков в канале и в трубе [1]:

– для потоков в канале

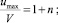(10)

– для потоков в трубе

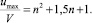(11)

С учетом приведенных зависимостей дефицит местной скорости для потока в трубе можно представить в виде:

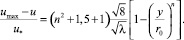(12)

Следует отметить, что вычисление дефицита местной скорости по (12) не требует каких-либо предположений о величине параметра Кармана κ, который необходим при использовании логарифмической формы дефицита (1) и (2). Сопоставление зависимостей (2) и (12) обнаруживает их очевидную на первый взгляд качественную разницу: зависимость (2), полученная на основе логарифмического профиля, указывает на то, что дефицит скорости является (при k = const) универсальной функцией y/r0, в то время как зависимость (12), полученная с использованием степенного профиля, указывает на то, что дефицит скорости существенным образом зависит от λ и n, то есть, по сути дела, сложным образом зависит от коэффициента гидравлического сопротивления. Выражения (2) и (12) могут согласовываться и даже совпадать друг с другом только в том случае, если влияние коэффициента λ, входящего в (12), некоторым образом компенсируется. С целью проверки данного предположения выполнен расчет дефицита местной скорости по соотношению (12) при различных значениях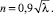

Анализ результатов расчета показывает (рис. 1), что дефицит местной скорости в трубах, рассчитанный по степенному профилю скорости, хотя по форме зависимости от y/r0 несколько отличается от функции (2) (см. рис. 1), оказался достаточно близким (при n = 0,1) к дефициту скорости, рассчитанному по профилю логарифмическому, причем даже весьма значительные изменения n не оказывают существенного влияния на дефицит местной скорости для течения в трубе.

Аналогичные расчеты могут быть выполнены для открытых широких каналов по зависимости:

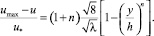(13)

Однако для вычисления дефицита по зависимости (13) необходима связь между n и .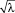

На основании анализа многочисленных опытных данных по распределению скоростей в трубах, каналах и в речных потоках опытным путем было установлено [5], что 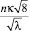есть величина постоянная, близкая к 1. Тогда можно считать, что при одинаковых коэффициентах сопротивления трубы и канала (λт = λк) показатели степени будут связаны с параметром Кармана следующим соотношением

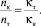(14)

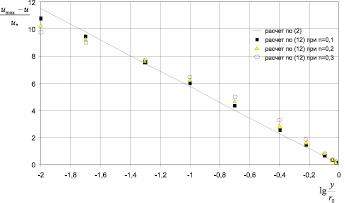
Рис. 1. Дефицит местной скорости для труб

Обработкой многочисленных опытных данных было установлено [6], что в основной толще потока в широких каналах 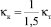, тогда при одинаковых значениях λк = λт с учетом (7) и (14) получаем для каналов:

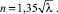(15)

Результаты расчета дефицита скорости по (13) для каналов приведены показаны на рис. 2.

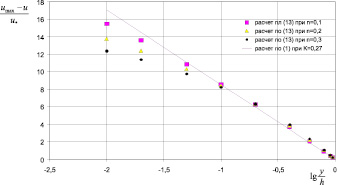
Рис. 2. Дефицит местной скорости для каналов

Таким образом, вопрос об описании распределения скоростей в каналах и трубах требует дальнейшего анализа. С этой целью используем известные данные о дефиците средней скорости в широких каналах (3) и в трубах (4). Дефицит средней скорости, определенный выше для потока в трубе в форме (4), запишем в виде:

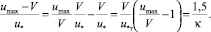(16)

Преобразуя выражение (16) с учетом соотношения (11) получаем следующее равенство:

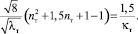(17)

Учитывая, что величина 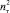имеет высший порядок малости по сравнению со вторым слагаемым, выражение (17) можно записать в виде:

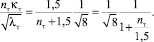(18)

Следует отметить, что в выражения (11) и (16) входит средняя скорость, найденная интегрированием профиля скорости по сечению трубы, которая несколько отличается от средней скорости, найденной по расходу. В то время как для широкого канала средняя скорость, определенная по расходу, совпадает со средней скоростью, полученной интегрированием профиля скорости по глубине потока.

Аналогичным образом, используя выражение (10) для дефицита средней скорости потока в широком канале, получаем:

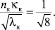(19)

Таким образом, соотношения (18) и (19), полученные аналитически из дефицита средней скорости, оказываются близкими (18) или практически совпадающими (19) с аналогичными соотношениями, полученными непосредственно обработкой профилей скорости [5]. Следует отметить также, что вследствие сравнительно небольшой величины 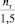по сравнению с единицей значение найденного комплекса 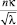для труб и каналов при одинаковых значениях входящих в него величин различается не сильно. Соотношения (17) и (19) можно представить также в виде 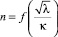. Так, для потоков в канале

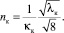(20)

Для потоков в трубе аналогичная зависимость имеет более сложный вид:

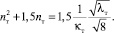(21)

Однако, учитывая, что величина 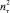существенно меньше, чем 1,5nт, из (21) можно считать, что и для течения в трубе

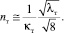(22)

Таким образом, оказывается, что показатель степени n в профилях скорости (5) и (6) для потоков в трубе и широком канале практически одинаковым образом связан с коэффициентом гидравлического сопротивления и параметром Кармана. Следует отметить также, что при κ = 0,4 из (22) получаем соотношение

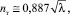(23)

которое близко к соотношению (7) Альтшуля–Нуннера.

Выражая из (17) величину, обратную параметру Кармана,

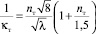(24)

и полагая, что соотношение (7) убедительно доказано, при подстановке его в (24) получаем:

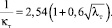(25)

Следует отметить, что вследствие того, что kт изменяется по поперечному сечению потока [6] с уменьшением kт в ядре потока по сравнению с пристенной зоной при анализе использовались осредненные по площади значения kср.

Сопоставляя выражение (25) с опытными данными, полученными обработкой измерений И. Никурадзе в гладких трубах [7], можно отметить, что характер связи между 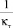и λт не подтверждается не только количественно, но также и качественно.

Это противоречие между расчетным и действительным поведением 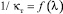можно преодолеть, предположив, что зависимость (7) Альтшуля−Нуннера является упрощенной аппроксимацией некоторой более сложной зависимости .

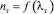Учитывая опытные значения kт при различных λт, осредненные по площади поперечного сечения (рис. 3), задавая значения λт, можно решением квадратного уравнения (21) определить значения nт, которое будет удовлетворять всему комплексу опытных данных и исключит отмеченное выше несоответствие выражения (25) опытным данным. Результаты решения уравнения (21) при различных 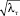приведены на рис. 4.

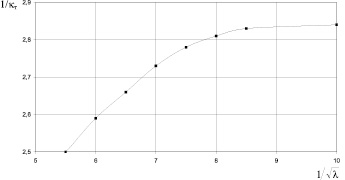
Рис. 3. Осредненное по сечению значение κ для гладких труб по опытным данным И. Никурадзе

Сопоставление результатов выполненного расчета с зависимостью (7) показывает, что они хорошо согласуются (рис. 4) лишь при малых значениях λт < 0,03, для которых значение 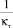изменяется незначительно. Для более широкого диапазона изменения λт аппроксимация, отражающая изменения 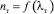, имеет более сложный вид:

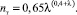(26)

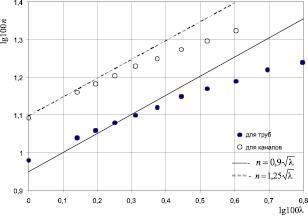
Рис. 4

Для потоков в широких каналах опытную проверку соотношения (20) удобно производить, записав его в виде:

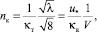(27)

где определение величины 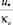может быть произведено без априорных предположений относительно величины параметра Кармана непосредственно по углу наклона линии тренда, полученной для каждого профиля скорости по опытным точкам в координатах u = f(ln y).

Это обстоятельство особенно важно при обработке натурных измерений в речных потоках, где прямое определение местной динамической скорости обычно невозможно вследствие трудности определения местного гидравлического уклона. Однако для речных потоков остаются сложности единообразного определения плоскости отсчета координаты y, поэтому при работе с такими профилями скорости целесообразно отдавать предпочтение измерениям в толще потока на значительном удалении от дна, где влияние неточности определения величины y уменьшается.

Результаты обработки профилей, измеренных на прямолинейных участках речных потоков различной водности в диапазоне значительных чисел Рейнольдса, согласуются с выражением (20) достаточно точно (рис. 5).

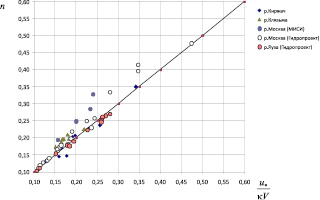
Рис. 5

Следует отметить, что для открытых, особенно речных, потоков имеющиеся сведения о параметре Кармана kк достаточно неопределенны и противоречивы. Вместе с тем по данным лабораторных измерений в открытых потоках, как уже отмечалось выше, было получено заметно меньшее значение kк в ядре потока по сравнению с параметром Кармана для течения в трубе, а также существенно большее значение показателя степени nк, при одинаковых значениях λ в открытом потоке по сравнению со значением пт для течения в трубе. Дополнительно к этому можно высказать следующие замечания, в общем согласующиеся с опытом. В непосредственной близости от дна канала формирование профиля скорости связано с генерацией турбулентности в этой зоне, которая слабо зависит от условий внешнего течения за пределами этого слоя, поэтому можно ожидать, что распределение скоростей здесь будет близким для трубы и широкого канала. Лабораторные измерения подтверждают это предположение [8]. В этом случае качественный характер зависимости параметра Кармана для этой зоны при течении в канале κ1к = f(λ), по всей видимости, будет таким же, как в трубах. За пределами этого слоя (при 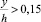) параметр Кармана, как уже отмечалось, в 1,5 раза меньше, чем в трубе. Проводя осреднение по глубине потока в широком канале с учетом этого соотношения найдем следующее соотношение между средним по сечению значением параметра Кармана и его значением в придонном слое:

κсрк = 0,0717κ1к, (28)

где k1к в придонном слое совпадает с параметром Кармана k1т в пристенной зоне трубы (рис. 3). Используя эти соображения в качестве исходных, сделаем попытку рассчитать nк, удовлетворяющее соотношению (20) и опытным данным по изменению κ1т = f(λ), которое предполагается таким же и для широких каналов.

Результаты расчетов nт и nк, представленные на рис. 4, согласующиеся с соответствующими выражениями (18) и (20), полученными из дефицита средней скорости и с полученными из опыта изменениями κ = f(λ) (рис. 3), обнаруживают одинаковую степень зависимости показателя n от λ и отличаются лишь числовым коэффициентом. При λ < 0,03 зависимости nт = f(λ) согласуются с опытной зависимостью Альтшуля−Нуннера для труб и с установленной экспериментально зависимостью для каналов [8]:

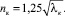(29)

Учитывая эквидистантность кривых, описывающих изменения n = f(λ) для потоков в трубах и в широких каналах в качестве аппроксимации для каналов, можно предложить выражение:

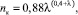(30)

достаточно точно отвечающее результатам расчета.

Выводы

1. С использованием степенного профиля скорости записаны выражения для дефицита местной скорости для потоков в трубах и каналах, анализ которых показал их устойчивость к изменению показателя степени в профиле скорости и малые расхождения с логарифмической формой записи дефицита местной скорости.

2. На основе анализа дефицита средней скорости для потоков в каналах и в трубах выявлен кинематический инвариант течения 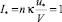, единый для осесимметричных потоков в трубах и плоских потоков в широких каналах, который может быть записан также в виде, объединяющем кинематические характеристики течения и коэффициент гидравлического сопротивления l:

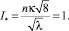
3. С учетом опытных данных, отражающих изменение параметра Кармана в зависимости от коэффициента сопротивления λ, получены уточненные зависимости n = f(λ) для потоков в трубах и каналах, отвечающие кинематическому инварианту течения и не противоречащие зависимостям, найденным ранее опытным путем.

Рецензенты:

Скворцов Л.С., д.т.н., руководитель ООО «Экотех – Москва», г. Москва;

Ханов Н.В., д.т.н., профессор кафедры гидравлики ФГБОУ ВПО «Московский государственный университет природообустройства», г. Москва.

Работа поступила в редакцию 11.01.2013.

Библиографическая ссылка