Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Штаборов Д.А. 1 Барабанов В.А. 1

---

1 ФГАОУ ВПО «Северный (Арктический) федеральный университет имени М.В. Ломоносова»

Исследование инерционных характеристик движения линеек из плоских сплоточных единиц (ПСЕ) в различных режимах (в частности в период разгона) необходимо для правильного выбора средств буксировки и перестановки линеек из ПСЕ, конструкций плотостоянок и их крепления, а также для более эффективного выполнения технологических и транспортных расчетов движения линеек из ПСЕ. В статье использовано математическое описание процесса разгона линеек из ПСЕ в виде уравнения регрессии. Составлен полный факторный план первого порядка с четырьмя переменными для определения приведенного гидродинамического сопротивления. Представлено уравнение регрессии при четырехфакторном эксперименте. Выполнена оценка воспроизводимости опытов, оценка значимости коэффициентов уравнения регрессии. Получена регрессионная модель с натуральными обозначениями факторов. Выполнен анализ полученной математической модели. Определена относительная погрешность вычисления времени и пути разгона моделей линеек из ПСЕ.

Статья в формате PDF

625 KB

плоская сплоточная единица

путь разгона

время разгона

приведенное гидродинамическое сопротивление

полный факторный план

уравнение регрессии

1. Войткунский Я.И. Сопротивление воды движению судов. – Л.: Судостроение, 1964. – 412 с.

2. Митрофанов А.А. О точности расчета инерционных характеристик плотов по разным методикам // Изв. вузов. Лесн. журн. – 2005. – № 6. – С. 48–56. – (Изв. высш. учеб. заведений).

3. Митрофанов А.А. Лесосплав. Новые технологии, научное и техническое обеспечение: монография. – Архангельск: изд-во АГТУ, 2007. – 492 с.: ил.

4. Митрофанов А.А., Камусин А.А. Моделирование и оптимизация процессов лесопромышленных производств: учебное пособие. – Архангельск: Изд-во АГТУ, 2003. – 118 с.:ил.

5. Перфильев П.Н. Проблемы лесосплава и методика исследований гидродинамических и инерционных характеристик линеек из плоских сплоточных единиц / П.Н. Перфильев, Д.А. Штаборов // Научное творчество молодежи – лесному комплексу России. Материалы IV всероссийской научн.-техн.конф. – Екатеринбург: Урал.гос.лесотехн.ун-т, 2008. – Ч.2. – С. 46–49.

6. Перфильев П.Н. Обоснование гидродинамических характеристик и технологических параметров линеек из плоских сплоточных единиц: дис. ... канд. техн. наук. – Архангельск, 2009. – 129 с.

7. Пижурин А.А., Розенблит М.С. Исследования процессов деревообработки. – М.: Лесн. пром-сть, 1984. – 232 с.:ил.

Совершенствование транспортных качеств линеек из плоских сплоточных единиц (ПСЕ) для их применения на малых и средних извилистых реках представляет интерес при технологических расчетах переместительных операций.

Целью представленной работы является получение инерционных характеристик и математической модели процесса неравномерного движения линеек из ПСЕ.

В настоящее время широко распространено использование математических методов планирования экспериментальных исследований на основе полных факторных планов. В данной теории используется математическое описание исследуемого процесса или объекта в виде уравнения регрессии, которое предоставляет широкие возможности по анализу изучаемого процесса или объекта и степени влияния на него каждого фактора.

Преобразовав выражения для определения времени и пути разгона плота постоянной силой в неподвижной жидкости при начальных значениях скорости v = 0 и времени t = 0[3], получаем зависимость для определения времени и пути разгона линейки из ПСЕ согласно методике [5] вида:

(1)

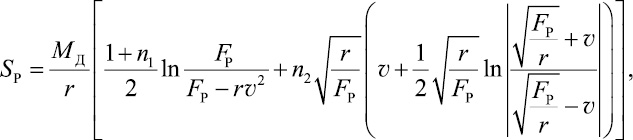(2)

где MД – масса древесины модели линейки из ПСЕ; r – приведенное гидродинамическое сопротивление воды движению модели линейки из ПСЕ; FР – усилие разгона модели линейки из ПСЕ; n1, n2,– параметры эмпирической формулы, которые были получены для определения коэффициента нестационарности n[1, 2, 3], определяемые по зависимостям:

где k – параметр, зависящий от характеристик линейки из ПСЕ, определяемый по зависимости:

где LМ – длина модели; BМ – ширина модели; TМ– осадка модели; ρ, ρД – плотность воды и древесины соответственно; v – скорость модели, равная [3].

Основными факторами, влияющими на величину гидродинамического сопротивления воды R движению модели линейки из ПСЕ, являются ее габаритные размеры и интервал между ПСЕ в линейке, а также скорость движения модели. Зависимость величины гидродинамического сопротивления воды R движению модели линейки из ПСЕ имеет вид [6]:

(3)

В зависимости (3) величина гидродинамического сопротивления воды R при постоянной скорости для каждой модели является функцией приведенного гидродинамического сопротивления, для определения которого составлен полный факторный план первого порядка с четырьмя переменными. Величина r в уравнении регрессии r = f(LМ, BМ, TМ, c) принята за выходной параметр. Входными параметрами являются: X1 – длина модели; X2 – ширина модели; X3 – осадка модели; X4– интервал между ПСЕ в модели.

Уравнение регрессии при четырехфакторном эксперименте имеет вид зависимости:

(4)

где x1x2x3x4 – входные факторы, соответственно длина, ширина, осадка модели и интервал между плитками ПСЕ в линейке в условном масштабе; b0 – свободный член; b1, b2, b3, b4 – коэффициенты при линейных членах; b12, b13, b14, b23, b24, b34 – коэффициенты, характеризующие парное взаимодействие; b123, b124, b234, b134 – коэффициенты, учитывающие взаимодействие трех членов; b1234 – коэффициенты, учитывающие взаимо­действие четырех членов.

В планах первого порядка каждый фактор варьируется на двух уровнях, то есть принимает в каждом опыте одно из двух значений: наименьшее или наибольшее. Нижний уровень факторов в условном масштабе обозначается –1, верхний + 1.

Необходимое и достаточное количество опытов N в эксперименте было определено по формуле [4]

N = 2m = 24 = 16,

где m – число факторов.

Размеры моделей и сочетание факторов для расчетной матрицы приведено в таблице.

Коэффициенты уравнения регрессии (4) рассчитаны по зависимости [4]:

Уравнение регрессии (4) после расчетов коэффициентов имеет вид:

(5)

С целью выяснения точности постановки экспериментов выполнена оценка воспроизводимости опытов по критерию Кохрена. Значение расчетного критерия Кохрена Gрасч = 0,192. По таблицам [7] определена величина табличного значения числа Кохрена Gтабл = 0,232. Так как Gрасч < Gтабл, то можно говорить об однородности дисперсий опытов, то есть все ошибки примерно одного порядка и допустимой величины.

Уравнение регрессии (4) имеет 16 коэффициентов bi. В каждом конкретном случае значимость этих коэффициентов и их влияние на выходной параметр r могут быть различными. Оценка значимости позволяет выявить так называемые незначимые коэффициенты, то есть те, которые в уравнении регрессии можно приравнять к нулю, так как значения этих коэффициентов соизмеримы с ошибкой определения bi. Оценка значимости была проведена с помощью критерия Стьюдента – tтабл [4, 7]. Для каждого коэффициента регрессии bi было вычислено экспериментальное значение tрасч. По таблицам [7] для уровня значимости q = 0,05 определена величина табличного значения критерия Стьюдента tтабл = 2. Проверено условие tрасч < tтабл для всех коэффициентов регрессии bi, не выполняется, следовательно, незначимых коэффициентов в уравнении регрессии, описывающем математическую модель эксперимента, нет.

Сочетание факторов

Далее была получена регрессионная модель с натуральными обозначениями факторов. При проведении экспериментов уровни варьирования факторов заданы в условном масштабе х. Значения х через Х определены по формулам [4]:

(6)

(7)

(8)

После подстановки формул (6), (7), (8) в уравнение регрессии (5) и несложных преобразований была получена зависимость:

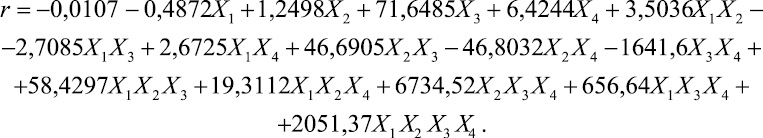(9)

С помощью зависимости (9) можно получить величину приведенного гидродинамического сопротивления воды r движению моделей линеек из ПСЕ. При подстановке входных факторов в натуральном масштабе измерения в интервалах варьирования, указанных в таблице.

Анализ полученной математической модели лучше всего проводить, пользуясь уравнением регрессии в нормализованных обозначениях факторов:

где L, B, T – длина, ширина и осадка линейки из ПСЕ; c – интервал между ПСЕ в линейке.

Важную информацию несут знаки коэффициентов регрессии, если линейный коэффициент регрессии положителен, то выходная величина возрастает с увеличением соответствующего фактора и убывает при его уменьшении. Также можно оценить относительную степень влияния варьируемых факторов на изменение выходной величины (относительную важность факторов). Чем больше величина tрасч, тем сильнее влияние соответст­вующего фактора на изменение выходной величины. Таким образом, на приведенное сопротивление воды r движению модели линейки из ПСЕ оказывают наибольшее влияние длина L и осадка T, наименьшее влияние оказывает интервал c.

Уравнение регрессии позволяет предсказать значение выходной величины для любой точки внутри области варьирования факторов. С его помощью можно строить графики зависимости выходной величины от любого фактора при фиксированных значениях остальных факторов.

Выполнены расчеты времени разгона tР (1) и пути разгона SР (2). Для модели линейки длиной модели – 0,65 м, шириной – 0,325 м, осадкой – 0,052 м, интервалом между ПСЕ – 0 м, состоящей из двух пятирядных ПСЕ время разгона составило с, при этом путь разгона равен SР = 1,7 мм. Модель линейки представлена на рисунке.

Модель линейки из двух пятирядных ПСЕ

Относительная погрешность вычисления времени разгона tР колеблется в интервале 0,002–4,68 %, а для пути разгона SР колеблется в интервале 0,042–4,79 %.

В заключение отметим, что приведенная математическая модель определения времени и пути разгона справедлива для линеек из ПСЕ длинной 13–44 м, шириной 4,5–6 м, осадкой 0,2–1 м и коэффициентом полнодревесности 0,42–0,49 при буксировке по малым и средним извилистым рекам с недостаточными глубинами.

Рецензенты:

Копейкин А.М., д.т.н., профессор кафедры лесопильно-строгальных производств Северного (Арктического) федерального университета имени М.В. Ломоносова, г. Архангельск;

Мясищев Д.Г., д.т.н., профессор кафедры транспортных машин Северного (Арктического) федерального университета имени М.В. Ломоносова, г. Архангельск;

Кирьянов Б.Ф., д.т.н., профессор кафедры прикладной математики и информатики, ФГБОУ ВПО «Новгордский государственный университет им. Ярослава Мудрого», г. Великий Новгород.

Работа поступила в редакцию 21.12.2012.

Библиографическая ссылка