Общие тенденции интенсификации современных производств направлены на рост качества готовой продукции, повышение энергоэффективности и производительности оборудования. В основе многих технологий производства целевого продукта лежит экстракция и другие процессы массопередачи. От правильного подхода к управлению аппаратом-экстрактороми грамотной реализации алгоритмов управления существенно зависят как технологические, так и экономические показатели качества системы управления процессом в целом.
При производстве шин в качестве присадки используются нефтяные экстракты «Норман». Присадку получают в экстракционной колонне путем очистки смеси нефтяных экстрактов от «тяжелой» фракции ФНЭТ, то есть их нормализации. Продукт является новейшей разработкой, превосходящей отечественные и зарубежные аналоги по показателям качества. В его закупке могут быть заинтересованы крупнейшие мировые производители шин Нокиан, Пирелли, Бриджстоун и другие.
В основе производства нормализированных экстрактов «Норман» лежит процесс жидкостной экстракции, характеризующийся нестационарностью и сложностью управления. Основным объектом управления выступает экстракционная колонна с системой входящих (исходный раствор и экстрагент) и отходящих (рафинат и экстракт) потоков. Рафинатом является раствор, из которого удалены экстрагируемые компоненты, а экстракт – раствор извлеченных веществ в экстрагенте, являющийся целевым продуктом.
Для решения оптимизационных задач в системах управления важно грамотно определить параметры, подлежащие оптимизации. Сделать это непросто, так как правильность выбора требуется сформулировать очень четко с применением количественной оценки [1]. Таким образом, важное условие правильной постановки оптимальной задачи заключается в наличии количественной оценки интересующего качества объекта оптимизации. Это условие также необходимо, так как только при его выполнении можно сравнивать эффекты от выбора тех или иных управляющих воздействий. Критерий оптимальности является количественной оценкой оптимизируемого качества объекта [2]. Вид критерия оптимальности определяется конкретным содержанием решаемой задачи оптимизации и иногда может оказывать существенное влияние на выбор метода решения. В конечном итоге достигаемое значение критерия оптимальности дает количественную оценку эффекта оптимизации.
Для успешного достижения цели оптимизации необходимо, чтобы критерий оптимальности действительно оценивал эффективность функционирования системы в заранее выбранном смысле. Это главное требование, определяющее корректность постановки задачи.
В модуле экстракции экстракционной колонны изложенным выше требованиям отвечают несколько частных критериев оптимальности:
● расход растворителя на вводе в колонну;
● расход сырья (смеси экстрактов) на вводе в колонну;
● массовая доля ФНЭТ в рафинатном растворе на выходе из колонны;
● массовая доля ФНЭТ в экстрактном растворе на выходе из колонны.
Расход сырья является производительностью данного модуля технологического процесса нормализации экстрактов. Изменение данного параметра строго регламентировано технологической частью проекта и ограничено нормами производительности пост- и предшествующего оборудования.
Исходя из материального баланса процесса экстракции [3, 4], массовые доли ФНЭТ в рафинатном и экстрактном растворах − взаимосвязанные величины, а значит, необходимость использовать оба критерия отсутствует.
Технологический процесс экстракции включает последующую регенерацию растворителя в каскаде испарителей с завершающей регенерацией в роторно-пленочном испарителе. Для обеспечения нормальных режимов работы данного оборудования требуется большое количество тепловой энергии (пара). При увеличении расхода растворителя на вводе в колонну значительно возрастают расходы на проведение экстракции, а, следовательно, и себестоимость продукции, занижает КПД всей установки, повышает трудозатраты на обслуживание оборудования. Данный частный критерий оптимальности включает экономические аспекты проведения процесса.
Содержание ФНЭТ в рафинатном растворе однозначно формирует показатель качества целевого продукта и принадлежит к технико-технологическим качественным частным критериям оптимальности.
Для предпочтительных частных критериев оптимальности (расход растворителя и массовая доля ФНЭТ в рафинатном растворе) в аналитическом виде сформулированы функции желательности и установлено соответствие между физическими и психологическими параметрами на основе психофизической функции желательности Харрингтона.
![]() (1)
(1)
![]() (2)
(2)
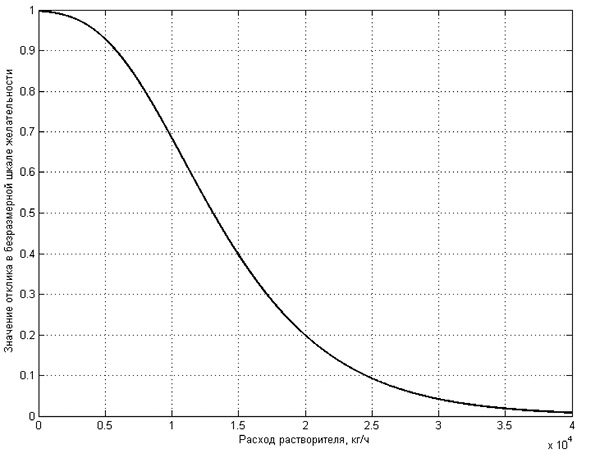
Рис. 1. Функция желательности для расхода растворителя на вводе в колонну
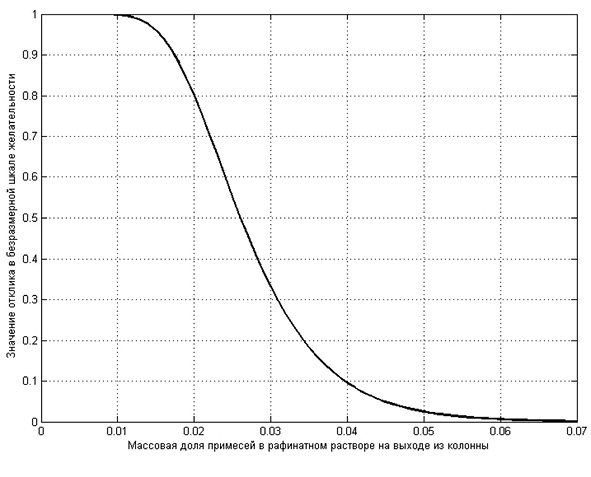
Рис. 2. Функция желательности для содержания примесей в рафинатном растворе на выходе из колонны
На основе частных функций желательности сформулирована обобщенная функция, которая является количественным, однозначным, единым и универсальным показателем качества исследуемого объекта управления, при детальном анализе свойств адекватности, эффективности и статистической чувствительности видится ее использование как целевой функции.
![]() (3)
(3)
Для текущего режима работы объекта управления с использованием математической модели (4) экстрактора [5] средствами моделирующего и оптимального алгоритмов формируется поверхность обобщенного отклика (рис. 3). Экстремум в заданной плоскости содержания ФНЭТ на вводе в колонну однозначно указывает на требуемое значение управляющего воздействия для функционирования объекта в условиях оптимума сформулированного обобщенного критерия оптимальности.
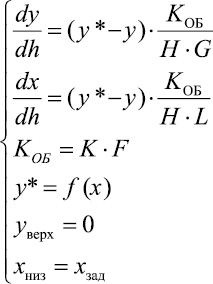 (4)
(4)
Таким образом, поставленная оптимизационная задача будет выглядеть следующим образом: «для текущего значения содержания примесей (ФНЭТ) в очищаемом потоке на вводе в колонну обеспечить максимум обобщенного критерия оптимальности».
Данные с измерительного прибора проточного рефрактометра поступают на верхний уровень АСУ ТП по протоколу MODBUS. Для определенного значения массовой доли ФНЭТ в очищаемом потоке на вводе в колонну определяется вид целевой функции (рис. 4) с однозначным экстремумом в рассматриваемом диапазоне в точке максимума обобщенного критерия оптимальности. Найденному оптимуму соответствует единственное значение компенсирующего управляющего воздействия расхода растворителя (экстрагента).
На базе моделирующего и оптимизационного алгоритма режима работы экстрактора разработана программная надстройка к промышленной SCADA-системе Siemens WinCC. Программный комплекс системы визуализации имеет мощный встроенный инструментарий для программирования на объектно-ориентированном языке Visual Basic for Application (VBA), используемый для локализации экстремума целевой функции.
Методы поиска оптимума, в которых для определения величины и направления шага поиска применялся предварительный анализ производных оптимизируемой функции по всем независимым переменным задачи, можно отнести к градиентным. Нахождение производных при наличии трудновычислимого критерия оптимальности связано с необходимостью выполнения большого объема вычислений, что может привести к существенному увеличению времени поиска.
Существует другая группа методов – безградиентные методы, использующие в процессе поиска информацию, получаемую не при анализе производных, а от сравнительной оценки величины критерия оптимальности в результате выполнения очередного шага. Такие методы обладают сравнительно простыми алгоритмами выполнения и легко реализуемы в рамках программного обеспечения микропроцессорной техники.
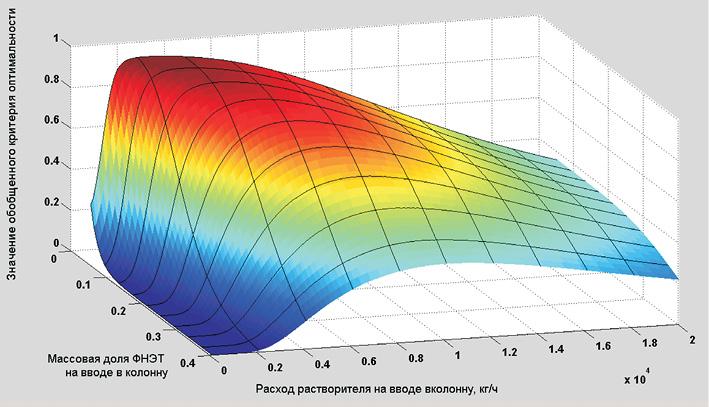
Рис. 3. Поверхность отклика
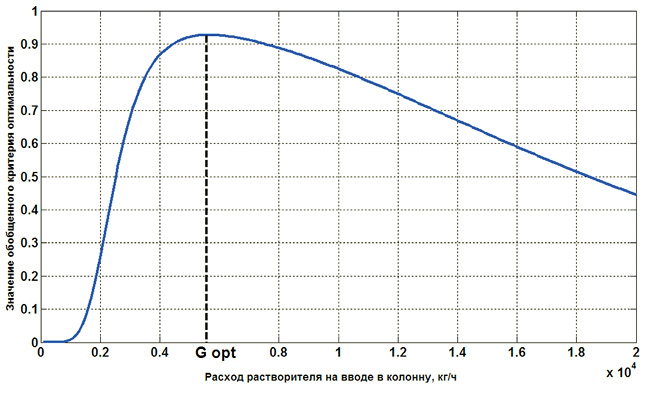
Рис. 4. График целевой функции при xниз = 0,2
Для текущей поставленной задачи оптимизации видится достаточным использование метода «золотого сечения» одномерного поиска по расходу растворителя. Второй параметр оптимизации (содержание примесей в рафинатном растворе) будет рассчитываться из математической модели колонны (4) по моделирующему алгоритму. Формула для оценки точности определения экстремума при заданном числе расчетов значений функции
![]() (5)
(5)
где Δ – абсолютная ошибка в определении положения экстремума после s вычислений значений целевой функции.
Решение поставленной задачи оптимизации в комплексе с использованием современной промышленной информационной системы визуализации и управления WinCC позволило не только обеспечить требуемое качество конечного продукта и уменьшение энергозатрат, но и разработать инвариантный промышленный продукт с применимостью под различные объекты управления – куда и направлен вектор развития современных промышленных систем управления технологическим процессом.
Рецензенты:
Сидягин А.А., д.т.н., профессор, Дзержинский политехнический институт, филиал Нижегородского государственного технического университета имени Р.Е. Алексеева, г. Дзержинск;
Сажин С.Г., д.т.н., профессор, генеральный директор ООО «НТЦ АСТ», г. Дзержинск.
Работа поступила в редакцию 26.11.2012.
Библиографическая ссылка
Липин И.А., Луконин В.П., Токарев С.В. ОПТИМАЛЬНАЯ СИСТЕМА УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМ ПРОЦЕССОМ ЖИДКОСТНОЙ ЭКСТРАКЦИИ // Фундаментальные исследования. 2013. № 1-1. С. 143-147;URL: https://fundamental-research.ru/ru/article/view?id=30906 (дата обращения: 18.12.2025).



