Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Завалищин Д.С. 1, 2

---

1 Институт математики и механики Уральского отделения Российской академии наук, Екатеринбург

2 Уральский федеральный университет имени первого Президента России Б.Н. Ельцина, Екатеринбург

В продолжении исследования задачи перемещения двухзвенного транспортного манипулятора в вязкой среде из начального положения в конечное с минимальными энергетическими затратами рассматриваются вопросы существования аналитического решения для системы дифференциальных уравнений, описывающих оптимальные траектории. Получены параметрические уравнения оптимальных перемещений. Проводится компьютерное моделирование, анализируются его результаты с физической точки зрения. Характерной особенностью является отсутствие непосредственной зависимости формы траектории от времени перемещения. Тем не менее его нельзя устремить к нулю, поскольку это вызовет значительное увеличение скорости перемещения и, как следствие, рост чисел Рейнольдса с выходом процесса за рамки ламинарного обтекания.

Статья в формате PDF

628 KB

динамическая система

управление

оптимизация

вязкая среда

1. Дыхта В.А., Самсонюк О.Н. Оптимальное импульсное управление с приложениями. – М.: Наука, ФИЗМАТЛИТ, 2000. – 256 с.

2. Завалищин Д.С. Энергосберегающие алгоритмы перемещения транспортного манипулятора в вязкой среде // Известия РАН. Теория и системы управления. – 1995. – № 2. – С. 169–174.

3. Завалищин С.Т., Чебан А.В. Транспортный манипулятор в вязкой среде: энергосберегающие алгоритмы перемещения // АиТ. – 1999. – № 12. – С. 166–175.

4. Завалищин Д.С., Завалищин С.Т. Динамическая оптимизация обтекания. – М.: Наука, ФИЗМАТЛИТ, 2002. – 224 с.

5. Завалищин С.Т., Сесекин А.Н. Импульсные процессы: модели и приложения. – М.: Наука, 1991. – 256 с.

6. Zavalishchin D.S. Optimization Setting of Slezkin’s Problem. Proceedings of the Steklov Institute of Mathematics. – M.: MAIK, «Nauka/Interperiodika», 2002. – Vol.8, № 2. – Р. 193–202

7. Zavalishchin D.S. Control Problems for a Body Movement in the Viscous Medium. From Physics to Control Through an Emergent View. World Scientific Series on Nonlinear Science, Editor: Leon O.Chua, University of California, Berkeley. – Series B. – 2010. – Vol. 15. – Р. 295–300.

Задача управления двухзвенным манипулятором в вязкой среде по критерию минимума энергетических затрат рассматривалась в [1, 3, 5]. Возникает интерес исследовать аналогичную задачу с точки зрения существования аналитических зависимостей для моделирования оптимальных траекторий перемещения манипулятора из начального положения в заданное при минимальных энергетических затратах. Такая постановка является актуальной для автономных манипуляторов [2]. Ситуация, в которой нужно исходить из весьма ограниченной энергетики мобильных манипуляторов, является естественной, а для автономных манипуляторов и неизбежной. Тогда с точки зрения теории динамической оптимизации обтекания [4, 6] актуальна следующая задача: найти законы изменения управляющих сил и моментов, обеспечивающие перемещение манипулятора из начального положения в заданное с ограниченными энергетическими затратами.

Постановка задачи

Рассматривается механическая система, состоящая из трех материальных точек O₀, O₁, O₂, соединенных между собой бесконечно тонкими абсолютно жесткими безынерционными стержнями с длинами r₁ и r₂ (рис. 1). Вся система располагается в вертикальной плоскости и может вращаться вокруг точки O0, а звено O₁O₂ – вокруг точки O₁. Такая система моделирует транспортный манипулятор (ТМ), предназначенный для перемещения грузов. При этом точки O₁, O₂ соответствуют центрам инерции первого и второго звена манипулятора соответственно. Транспортируемый груз входит в состав второго звена.

Элементы ТМ связаны цилиндрическими шарнирами в точках O₀, O₁, в которых действуют создаваемые внутренними силами управляющие моменты U₁, U₂.

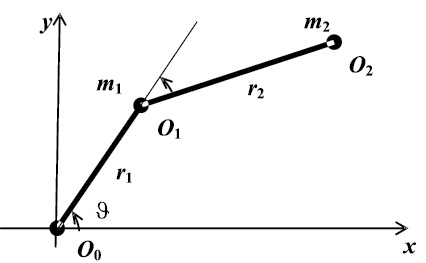
Рис. 1. Двухзвенный манипулятор

Силы тяжести m₁g и m₂g, силы сопротивления среды D₁ и D₂ и силы Архимеда приложены к первому и второму звену соответственно.

Введем следующие обобщенные координаты ТМ: φ, υ – величины, характеризующие угловое положение звеньев O₀O₁, O₁O₂ соответственно. Тогда координаты точек O₁, O₂ можно определить формулами:

Уравнения движения ТМ имеют вид [4]:

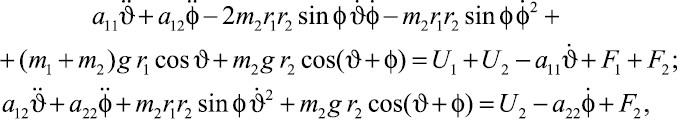(1.1)

где

Выражение для мощности выписывается в форме:

(1.2)

Теперь можно поставить задачу о нахождении оптимальных управляющих моментов при перемещении ТМ из начального состояния в заданное с ограничениями на работу A(T).

Нахождение оптимальных траекторий

Введем обозначения:

(2.1)

После решения задачи минимизации работы по перемещению манипулятора получим двухточечную краевую задачу [4]:

(2.2)

с начальными условиями

(2.3)

где

(2.4)

Обозначим постоянные

Тогда В системе (2.2) постоянные c1 и c2 подбираются так, чтобы выполнялись краевые условия (2.3). Таким образом, эти постоянные являются функциями от набора значений переменных {z10, z1T, z30, z3T} в начальный и конечный моменты времени.

Если переписать систему (2.1) в виде

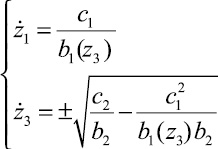(2.5)

при тех же начальных условиях (2.3) и рассмотреть невырожденный случай, когда z3T ? z30, то возникают два варианта. В первом из них z_3T ≥ z₃₀, и в уравнении системы (2.5) выбирается знак плюс, во втором, при z_3T ≤ z₃₀, выбирается знак минус. Далее без ограничения общности можно считать, что реализуется первый вариант. С учетом соотношения (2.4) и введенных обозначений можно решить второе уравнение системы (2.5). Перепишем его в виде

(2.6)

Отсюда получим

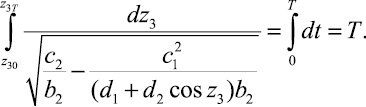(2.7)

Введем обозначение или . Тогда систему (2.2) можно записать в виде

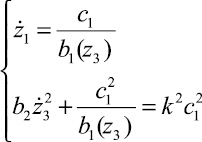(2.8)

или

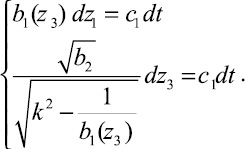(2.9)

Таким образом, фазовая траектория системы

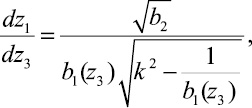(2.10)

то есть не зависит от константы c1.

Моделирование оптимального управления

Полученная задача (2.8), (2.9) решается численно. Моделирование экстремальных программ позволит качественно оценить поведение исследованной системы [7]. Находятся оптимальные значения параметров c1k, которые определяют оптимальное движение манипулятора в соответствии с уравнениями (2.5). Само оптимальное управление определяется соотношениями (1.1).

При численном решении задачи нужно учитывать, что функции f₁(z₃, c₁, k), f₂(z₃, c₁, k) должны быть определены и действительны на интервале [z₃₀, z_3T], что дает дополнительные ограничения на постоянные.

На рис. 2 показано оптимальное движение двухзвенного манипулятора при следующих исходных данных:

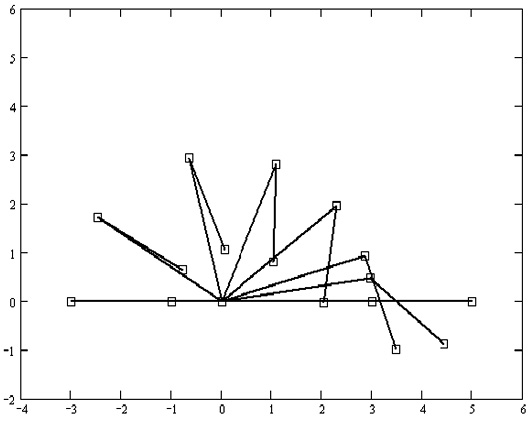
Рис. 2. Оптимальные перемещения ТМ (m₁ = 0,1; m₁ = 1,0 )

На рис. 3 показано оптимальное движение двухзвенного манипулятора при других исходных данных, масса второго звена меньше массы первого.

В результате решена задача построения оптимальных программ перевода транспортного манипулятора из начального положения в заданное при ограничениях на затраченную работу.

Исследования выполнены при финансовой поддержке РФФИ, проект № 10-01-00356 и в рамках программы фундаментальных исследований Президиума РАН «Математические модели и алгоритмы в управляемых системах с нелинейной динамикой» при поддержке УрО РАН, проект № 12-П-1-1012/1.

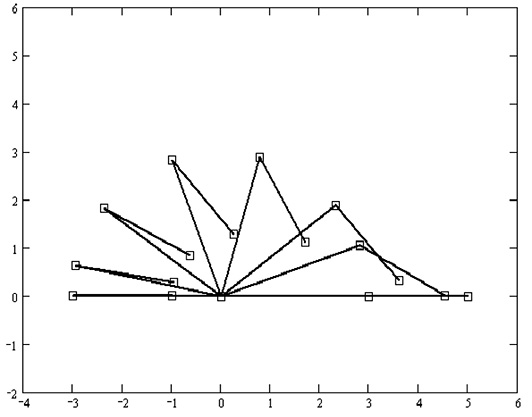
Рис. 3. Оптимальные перемещения ТМ (m₁ = 0,1; m₁ = 1,0 )

Рецензенты:

Тимофеева Г.А., д.ф.-м.н., профессор, зав. кафедрой, УрГУПС, г. Екатеринбург;

Сесекин А.Н., д.ф.-м.н., профессор, в.н.с., ИММ УрО РАН, г. Екатеринбург;

Попов Ф.А., д.т.н., профессор, зам. директора по информационным технологиям, Бийский технологический институт (филиал) ГОУ ВПО «Алтайский государственный технический университет им. И.И. Ползунова», г. Бийск.

Работа поступила в редакцию 13.11.2012.

Библиографическая ссылка