Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Галушкин Н.Е. 1, 2 Язвинская Н.Н. 3 Галушкина И.А. 4

---

1 ФГБОУ ВПО «Южно-Российский государственный университет экономики и сервиса», Шахты

2 ФГАОУ ВПО «Новошахтинский филиал Южного федерального университета», Новошахтинск

3 ФГБОУ ВПО «Южно-Российский государственный университет экономики и сервиса», Шахты

4 ФГАОУ ВПО «Новошахтинский филиал Южного федерального университета», Новошахтинск

В экспериментах использовались аккумуляторы фирмы «SAFT» стационарного применения длительного режима разряда. Разряд аккумуляторов выполнялся до напряжения 1 В при постоянных токах разряда от 0,1Cn (Cn – номинальная емкость аккумулятора) до токов разряда, при которых отдаваемая аккумулятором емкость была близка к нулю. Заряд аккумуляторов выполнялся в соответствии с инструкцией по их эксплуатации. Было доказано, что для аккумуляторов фирмы SAFT стационарного применения длительного режима разряда эмпирические уравнения Коровина−Скундина, обобщенное уравнение Пейкерта, уравнение пористого электрода и интеграл вероятности описывают изменение емкости аккумуляторов при различных тока разряда при одних и тех же параметрах независимо от емкости исследуемых аккумуляторов. В то время как уравнения Пейкерта и Агуфа справедливы только от точки перегиба экспериментальной кривой С(i) и до бесконечности. Уравнение Либенова не может быть использовано для вычисления емкости щелочных аккумуляторов.

Статья в формате PDF

392 KB

аккумулятор

никель-кадмиевый

эмпирические уравнения

емкость

ток разряда

1. Агуф И.А. Некоторые вопросы теории пористого электрода и процессы, протекающие в свинцовом аккумуляторе: сб. работ по ХИТ. – Л.: Энергия, 1968. – С. 87–100.

2. Беляев Б.В. Разряды химических источников тока при постоянной силе тока // Электротехника. – 1968. – № 3. – С. 35–38.

3. Структурное моделирование работы аккумуляторов: монография / Н.Е. Галушкин, Н.Н. Язвинская, Ф.И. Кукоз, Д.Н. Галушкин. – Шахты: Изд-во ЮРГУЭС, 2009. – 191 с.

4. Галушкин Н.Е. Моделирование работы химических источников тока: монография.– Шахты: Изд-во ДГАС, 1998. – 224 с.

5. Дасоян М.А., Агуф И.А. Основы расчета конструирования и технологии производства свинцовых аккумуляторов. – Л.: Энергия, 1978. – 150 с.

6. Коровин Н.В., Скундин А.М. Химические источники тока: справочник.– М.: МЭИ, 2003. – 733 с.

7. Маделунг Э. Математический аппарат физики.– М.: Мир, 1961.– 620 с.

8. Селицкий И.А., Герчиков Б.А., Константинов М.М. Производство свинцовых аккумуляторов.– М.: Госэнергоиздат, 1947.– 216 с.

9. Peukert W. Uber die Abhangigkeit der Kapazitat von der Entladestromstarke bei Bleiakkunzalatoren // Elektrotechn. Z. – 1987. – № 20. – P. 345–251.

В данной работе исследуем возможность применения наиболее известных эмпирических соотношений для оценки емкости аккумуляторов фирмы «SAFT» стационарного применения длительного режима разряда. А именно соотношений:

– Пейкерта [9]

(1)

– Либенова [5]

(2)

– Агуфа [1]

(3)

– Коровина-Скундина [6]

(4)

– Обобщенного Пейкерта [3]

(5)

– Интеграла вероятности

(6)

Процесс разряда аккумуляторов является фазовым переходом, а фазовые переходы часто описываются интегралом вероятности [7]. Поэтому проанализируем и эту зависимость.

– Уравнение пористого электрода [4]

(7)

где C – отдаваемая емкость; i – ток разряда; A, B, D, s, i₀, n, a0, a1, a2… – эмпирические константы. C_m – максимальная емкость аккумулятора. Последняя зависимость была получена из расчета распределения тока по глубине пористого электрода при различных токах разряда. Существует много и других менее используемых методов расчета отдаваемой аккумулятором емкости [2, 8]. Однако они, как правило, являются частными случаями соотношений (1)–(7) или их комбинациями.

Экспериментальная часть

В экспериментах использовались аккумуляторы фирмы «SAFT» стационарного применения длительного режима разряда.

Разряд аккумуляторов выполнялся до напряжения 1 В, так как при более низких напряжениях, как правило, не работают внешние устройства, подключенные к данному аккумулятору, поэтому отдаваемая емкость при этих, более низких напряжениях, не имеет практического значения. Заряд аккумуляторов выполнялся в соответствии с инструкцией по их эксплуатации.

Перед изменением разрядного тока, чтобы исключить взаимное влияние одного исследуемого зарядно-разрядного цикла на другой (через всевозможные остаточные явления, эффект «памяти» и т.д.), проводились от одного до трех контрольно-тренировочных циклов. Емкость аккумулятора, полученная после каждого контрольно-тренировочного цикла, сравнивалась с первоначальной емкостью. Если полученная емкость отличалась более чем на 10 %, выполнялись дополнительные контрольно-тренировочные циклы. Тем самым обеспечивались одинаковые начальные условия для всех исследуемых зарядно-разрядных циклов. Контрольно-тренировочные циклы выполнялись в соответствии с инструкцией по эксплуатации исследуемых аккумуляторов.

При каждом токе разряда проводились три зарядно-разрядных цикла. Если разрядная емкость не сильно различалась в этих циклах (не более 5 %), то в качестве экспериментальной разрядной емкости при исследуемом токе разряда бралось среднее значение. В противном случае снова выполнялись контрольно-тренировочные циклы по методике, описанной выше, и эксперимент повторялся заново. Результаты экспериментальных исследований представлены на рис. 1. Емкость находилась при токах разряда от 0,1Cn и до токов, при которых отдаваемая емкость была близка к нулю.

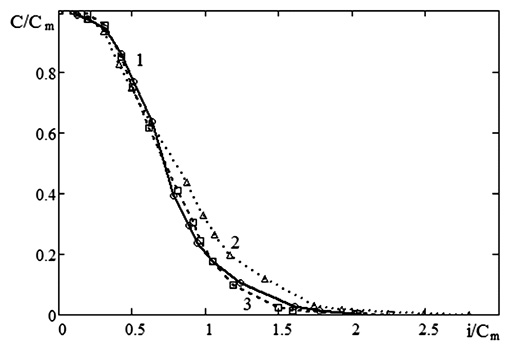
Рис. 1. Зависимости емкости аккумуляторов от токов разряда:1 – аккумулятор SBLE 7.5; 2 – аккумулятор SBLE 47; 3 – аккумулятор SBLE 110; Cm – максимальная емкость аккумуляторов

На рис. 1 результаты нормированы на максимальную емкость аккумуляторов. Данная емкость находилась при токах разряда 0,1C_n. Нормировка результатов на максимальную емкость позволила учесть и нивелировать разброс по емкости, который есть у любых аккумуляторов даже одного типа и одной и той же номинальной емкости.

В нормированных координатах все три кривые эквивалентны, так как их доверительные интервалы перекрываются. Данный экспериментальный факт однозначно следует из того, что у всех исследуемых аккумуляторов одни и те же электроды одной толщины ламельного типа. Различие в аккумуляторах различной емкости заключается только в площади электродов и в их числе. Таким образом, в нормированных координатах параметры любого аккумулятора должны быть эквивалентны параметрам аккумулятора единичной емкости с теми же электродами, и, следовательно, все кривые типа рис. 1 должны совпадать в пределах статистической погрешности, что и наблюдается в экспериментах.

Соотношения (1)–(3) не могут описать экспериментальные кривые рис. 1 на всем интервале изменения токов разряда. Во-первых, экспериментальные кривые вблизи нуля выпуклые, а соотношения (1)–(3) дают только вогнутые кривые (при положительных значениях всех констант). Во-вторых, для соотношений (1), (3) при i → 0 получаем C → ∞, что лишено физического смысла. Поэтому сначала исследуем применимость соотношений (4)–(7) для описания зависимости емкости аккумуляторов от токов разряда.

Оптимальные параметры для соотношений (4)–(7), соответствующие указанным экспериментальным данным, находились по методу наименьших квадратов с использованием процедуры оптимизации Левенберга-Маркардта и представлены в табл. 1.

Таблица 1

Оптимальные параметры эмпирических соотношений (4)–(7) для аккумуляторовфирмы «SAFT» с длительным режимом разряда

В табл. 1 S – среднеквадратичное отклонение экспериментальных точек относительно оптимальной кривой; d – относительная погрешность в процентах.

Из табл. 1 видно, что параметры соотношений (4)–(7) очень слабо меняются для различных типов аккумуляторов, несмотря на то, что емкость аккумуляторов изменяется более чем в десять раз. Это связано с тем, что нормированные экспериментальные кривые аккумуляторов SBLE 7.5, SBLE 47, SBLE 110 практически совпадают (рис. 1). Поэтому найдем средние оптимальные параметры для каждого из соотношений (4)–(7), используя экспериментальные данные сразу для всех аккумуляторов SBLE 7.5, SBLE 47, SBLE 110 по методу наименьших квадратов. Результат представлен в последнем столбце табл. 1.

Из табл. 1 видно, что уравнения (4)–(7) правильно отображают экспериментальные данные при любых токах разряда с относительной погрешностью менее 6–8 %, что вполне достаточно для практических целей.

Таким образом, для аккумуляторов фирмы «SAFT» стационарного применения длительного режима разряда эмпирические уравнения Коровина-Скундина, обобщенное уравнение Пейкерта, уравнение пористого электрода и интеграл вероятности описывают изменение емкости аккумуляторов при различных токах разряда при одних и тех же параметрах независимо от емкости исследуемых аккумуляторов.

Теперь рассмотрим применимость уравнений Пейкерта (1), Агуфа (3), Либенова (2) для данных аккумуляторов. В силу обратно пропорциональной зависимости емкости аккумуляторов от тока разряда в уравнениях (1)–(3) они могут быть использованы только начиная от точки перегиба функции C(i) рис. 1 и до бесконечности. Для аккумуляторов SBLE точка перегиба кривой C(i) находится примерно при токе разряда i = 0,8C_n. В связи с этим проверим применимость уравнений Пейкерта, Агуфа и Либенова для рассматриваемых аккумуляторов в интервале токов разряда от i = 0,8C_n и до i = 2,8C_n (2,8C_n – наибольшие токи в наших экспериментальных исследованиях). С этой целью найдем оптимальные параметры для этих уравнений по экспериментальным данным (рис. 1). Результаты представлены в табл. 2.

Таблица 2

Оптимальные параметры эмпирических соотношений Пейкерта, Агуфа и Либенова для токов разряда от i = 0,8C_n и до i = 2,8C_n

Из табл. 2 видно, что в данном интервале изменения токов разряда уравнения Пейкерта и Агуфа хорошо соответствуют экспериментальным данным, относительная погрешность менее 3,5 и 2 % соответственно, что вполне достаточно для практических целей. Таким образом, уравнения Пейкерта и Агуфа могут быть использованы для практических расчетов емкости, отдаваемой щелочными аккумуляторами SBLE в интервале токов разряда от i = 0,8Cn до бесконечности рис. 2 и 3.

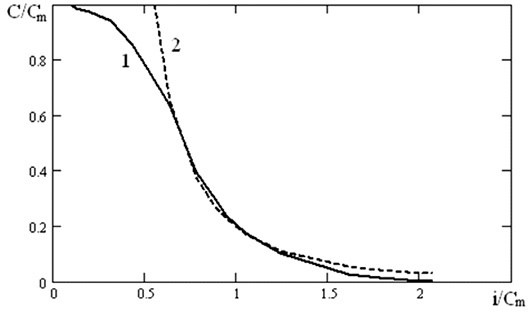
Рис. 2. Зависимость емкости аккумулятора SBLE 7.5 от тока разряда:1 – экспериментальная кривая; 2 – оптимальная кривая для уравнения Пейкерта (1) в интервале токов разряда от i = 0,8C_n и до i = 2,8C_n

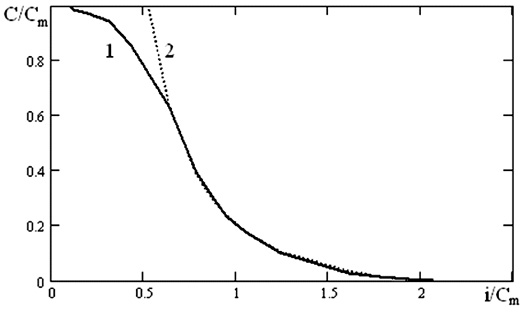
Рис. 3. Зависимость емкости аккумулятора SBLE 7.5 от тока разряда:1 – экспериментальная кривая; 2 – оптимальная кривая для уравнения Агуфа (3) в интервале токов разряда от i = 0,8C_n и до i = 2,8C_n

Уравнение Либенова в данном интервале изменения токов разряда плохо соответствует экспериментальным данным, относительная погрешность 11 %. Таким образом, уравнение Либенова имеет еще более частный характер, чем уравнения Пейкерта и Агуфа, и область применения его значительно уже.

Библиографическая ссылка