В мировой промышленности широкое распространение имеют композитные материалы, биметаллы. Сочетание разных металлов (железо, серебро, никель, медь, алюминий) используют для создания антикоррозионных поверхностей, термочувствительных элементов, силовых проводников и проводов связи [1]. Расположение меди в наружном слое, а алюминия или стали внутри конструкции определяется следующим: с одной стороны, при переменном токе достигается более высокая проводимость всего провода в целом, с другой – медь защищает расположенный под ней металл от коррозии. Как показывают сравнительные характеристики, провод, изготовленный из омедненной алюминиевой проволоки, представляет собой экономически выгодную замену полностью медному проводу в широком диапазоне областей применения:
– коаксиальные кабели для систем кабельного телевидения, передачи видеоизображений и информации, линий передачи сигнала в телекоммуникационных сетях, провода для магистральных распределительных линий;
– компоненты для электрических трансформаторов, электронных приборов, бытовых электрических устройств;
– автомобильные, установочные провода.
Применение оболочек при прессовании трудно деформируемых материалов, к которым можно отнести и сплавы алюминия, в ряде случаев обоснованно [3].
Однако на сегодняшний день изделия из «биметалла» алюминий в медной оболочке обладают существенным минусом – являются хрупкими и ломкими при небольших радиусах изгиба. Применение процесса прессования направлено на повышение пластических свойств изделия за счёт наиболее благоприятной схемы напряжённо-деформированного состояния в области деформации.
Совместное истечение разнородных материалов при прессовании требует дополнительных исследований. Для того чтобы получить желаемое качество продукции, требуется тщательно выбрать параметры процесса: толщину оболочки, форму инструмента и трение и др. Это требует большого количества экспериментов и теоретических исследований с применением математического моделирования. Моделирование позволяет существенно сократить финансовые и временные расходы при решении данной задачи. Все большее распространение находят численные методы анализа напряженно-деформированного состояния в программных системах, в основах которых положено использование метода конечных элементов, таких как ANSYS, ABAQUS, QForm, DEFORM и др. Моделирование процессов обработки металлов давлением позволяет проводить всесторонние исследования, так как позволяет изменять базовые параметры модели в широком диапазоне.
В статье рассматривается влияние инструмента, напряжений и трения при одинаковой толщине оболочки на качество получаемого изделия и его механические свойства. Известно [4], что влияние формы инструмента на процесс истечения при увеличении толщины стенки снижается. Поэтому для исследования была выбрана толщина оболочки, равная 0,1 диаметра заготовки. Показано, что, несмотря на небольшую толщину, оболочка значительно изменяет очаг деформации и напряженно-деформированное состояние деформируемых заготовок.
Целью работы является изучение напряженно-деформированного состояния биметалла при прессовании через ступенчатую матрицу сложной формы. Из работы [2] известно, что для случая, когда величина трения составляет μ = 0,2, оптимальными углами матрицы для прессования заготовки с первоначальным диаметром D = 40 мм и диаметром готового изделия d = 20 мм является α = 29°, а для ступенчатой матрицы ‒ α = 25,3° и β = 31,5°. Однако немаловажное значение играет и форма матрицы. Эти данные послужили основой для проверки 11 возможных форм матриц (рис. 1).
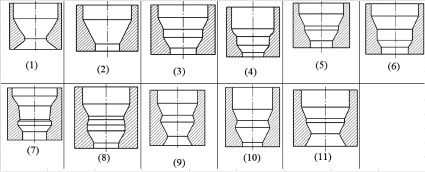
Рис. 1. Формы матриц
На рис. 1 показаны: матрица (1) «преломлённой» формы с круглым калибрующим пояском; (2) – простая однозаходная матрица с оптимальным углом [2]; ступенчатые матрицы оптимальной формы (3) [2] и формой с углами в 45° (4); (5) и (6) – ступенчатые матрицы с разной длинной промежуточного калибрующего пояска. Матрицы (3) и (6) отличаются тем, что диаметр первой ступени у матрицы (6) не симметричен, т.е. калибрующая ступень начинается с диаметра 32 мм, у (3) матрицы – 30 мм. (7), (8), (9) и (10) – матрицы сложной формы с «обратным» промежуточным калибрующим пояском. Форма (11), похожая на форму матрицы (5), но отличающаяся от нее закругленным калибрующим пояском второй ступени. Коэффициент вытяжки для всех матриц равен 4. Изготовление матриц сложной формы, а также проведение экспериментов, требует значительных затрат времени и материальных ресурсов. Поэтому моделирование было выбрано как метод исследования. Для компьютерного моделирования был выбран пакет ABAQUS/CAE Student Edition. Заметим, что система ABAQUS/CAE представляет собой очень гибкий и мощный инструмент для исследования процессов ОМД. Теоретические основы, заложенные в систему, позволяют рассматривать значительное количество параметров, необходимых для построения картины напряженно-деформированного состояния.
Для оценки напряженно-деформированного состояния в системе ABAQUS/CAE встроены следующие показатели [5].
Показатель напряженного состояния:
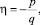
где p – интенсивность нормальных напряжений; q – среднее нормальное напряжение.
Накопленная интенсивность деформации [4]:
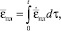
где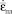 
– скорость пластической дефор-
мации.
Эти два параметра являются ключевыми для расчета поврежденности.
В качестве модели деформируемого материала был выбран алюминий марки АМг6 в медной оболочке. Механические свойства материала были заданы с использованием модели пластичности Джонсона‒Кука с деформационным и скоростным упрочнением и термическим разупрочнением [6]. Ввели также зависимость предела текучести от показателя напряженного состояния, накопленной интенсивности деформации и температуры.
Предел текучести
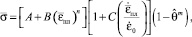
где A, B, n, m, C,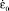 
– параметры модели.
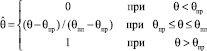
где θпр – температура перехода; θпл – температура плавления.
В соответствии с моделью разрушения Джонсона‒Кука разрушение происходит тогда, когда параметр поврежденности ω достигает единицы.
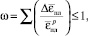
где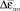 
– приращение накопленной интенсивности деформации; 
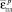– предельная деформация при разрушении.
Предельная деформация при пластическом разрушении также зависит от показателя напряженного состояния, накопленной интенсивности деформации и температуры.
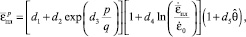
где d1, d2, d3, d4, d5 – параметры модели разрушения.
На рис. 2 изображены кривые, описывающие механические свойства алюминия марки АМг6 и меди по Джонсону‒Куку. Данные кривые отражают зависимость предела текучести от накопленной интенсивности пластической деформации.
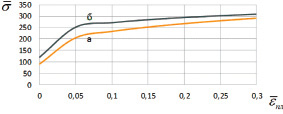
Рис. 2. Кривые течения деформируемых материалов:
а – медь; б – алюминий (АМг6)
Мониторинг значений показателей напряженно-деформированного состояния осуществлялся в центральной зоне и периферии (рис. 3). Одна точка в центральной зоне сердечника, одна точка на границе раздела сердечника и оболочки, относящаяся к сердечнику, одна точка на границе раздела сердечника и оболочки, относящаяся к оболочке, и еще одна точка на границе контакта оболочки и инструмента.
В общей сложности были проведены 22 численных эксперимента. В каждом случае менялась геометрия инструмента, и для каждой формы матрицы осуществлялось два эксперимента, менялось значение коэффициента трения. Между сердцевиной и оболочкой задавался коэффициент трения, равный единице, тем самым осуществлялось ограничение, когда две поверхности полностью прилипают друг к другу. Задача решалась в осесимметричной постановке.
Для каждой матрицы был рассчитан параметр поврежденности. Результаты для наглядности сведены в графики.
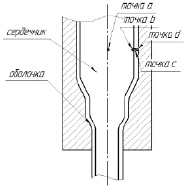
Рис. 3. Схема биметалла
Согласно графику на рис. 4 для случая, когда коэффициент трения между инструментом и оболочкой был равен 0,2, наихудшие результаты оказались у матриц (1), (7) и (11). Наилучшие результаты показали (3), (5), (6) и (10) матрицы. Это показывает, что применение обычной двухступенчатой (3) матрицы с длинным калибрующим пояском после первой ступени при смазке с коэффициентом трения 0,2 с оптимальными углами дает хороший результат. Вместе с тем применение матрицы (6) дает наименьшее значение параметра из представленных. Видно, что уменьшение диаметра первого калибрующего пояска на 5 % позволило снизить значение поврежденности в самой опасной точке b на 7,6 %. Применение же матриц сложной формы с «обратным» промежуточным пояском не оправдало себя. Единственной матрицей с хорошими результатами была (10), но затраты на изготовление такой формы окажутся выше, чем при изготовлении обычной двухступенчатой матрицы (3), либо (6).
а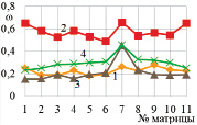 
б 
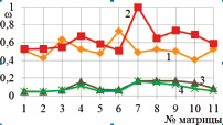
Рис. 4. Параметр поврежденности:
а – коэффициент трения 0,2;
б – коэффициент трения 0,1 (1 – точка а, 2 – точка b, 3 – точка c, 4 – точка d)
Для коэффициента трения 0,1 на рис. 5 наихудшие величины параметра поврежденности показали матрицы (7), (4) и (6). Лучшие значения параметра оказались у матриц (1), (2), (5) и (11). Т.е. применение обычной одноступенчатой матрицы с оптимальным углом более чем оправдано. Однако в случае применения смазки с коэффициентом трения 0,1 показатель поврежденности в сердечнике выше, чем при смазке с коэффициентом трения 0,2. Самой оптимальной формой матрицы оказалась (6), причем только для коэффициента трения 0,2, так как снижение трения только ухудшило качество готового
изделия.
В качестве дополнительной проверки адекватности оценки поврежденности по методу Джонсона‒Кука была построена диаграмма пластичности и пути деформирования (рис. 5) в точках, где показатель поврежденности был максимальным, т.е. a и b. Как видно из диаграммы в точке b для неоптимальной матрицы (7) произошло исчерпание ресурса пластичности, которое привело к образованию дефектов и разрушению.
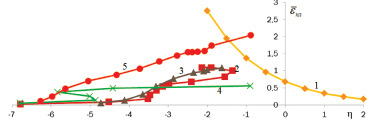
Рис. 5. Диаграмма пластичности и пути деформирования частиц материала в точках:
2 – точка a для матрицы (6); 3 – точка b для матрицы (6);
4–точка a для матрицы (7); 5 – точка b для матрицы (7)
Образование дефектов можно наблюдать и визуально в постпроцессоре. На рис. 6 визуально сравниваются распределение интенсивности нормальных напряжений (а) и показателя поврежденности (б) для оптимальной формы матрицы (правая половина) и неоптимальной (левая половина).
а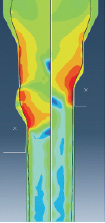 
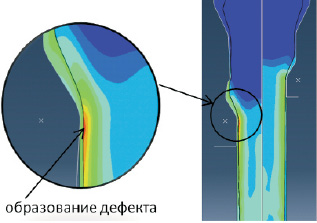б
Рис. 6. Картина напряженно-деформированного состояния:
а – распределение интенсивности нормальных напряжений;
б – распределение показателя поврежденности по Джонсону‒Куку
Всестороннее изучение показателей напряженного состояния позволяют оценивать качество изделия при разных технологических показателях, тем самым возможен выбор оптимальных характеристик инструмента и условий. Это очень важно, так как применение технологий, улучшающих качество, создает конкурентно-способную продукцию. Тем более что моделирование в отличие от метода «проб и ошибок» позволяет значительно экономить время и денежные средства.
Заключение
Биметаллическая проволока – это пример эффективности композитных материалов. Этот продукт сочетает в себе лучшие характеристики меди и алюминия (меди и стали), обеспечивает значительную экономию в области кабельно-проводниковой продукции.
Было проведено исследование, направленное на выбор оптимальной матрицы сложной формы для прессования биметаллического прутка из алюминия в медной оболочке. Для реализации этой работы был использован метод моделирования в системе ABAQUS/CAE. Данная система позволяет проводить расчеты с возможностью гибкой настройки модели материала. Модель материала поддерживает деформационное и скоростное упрочнение и термическое разупрочнение, а также возможно задавать модель пластического разрушения с вычислением параметра поврежденности.
Все это направленно на изучение напряжено-деформированного состояния, которое, основываясь на критерии оценки поврежденности, дает возможность делать предварительные оценки качества изделия. Тем самым выявляется адекватность применения тех или иных технологических условий и параметров инструмента.
Оптимальная форма геометрии инструмента и соответствующие параметры процесса выдавливания направлены на повышение механических свойств биметаллических проводников, в данной работе ‒ на повышение пластичности. Что позволит существенно повысить конкурентность алюмомедных проводников к медным проводникам, в свою очередь расширяя область применения, биметаллических проводников.
Рецензенты:
Поляков А.П., д.т.н., доцент, ведущий научный сотрудник лаборатории системного моделирования Института машиноведения УрО РАН, г. Екатеринбург;
Петунин А.А., д.т.н., доцент, зам. директора по научной работе Механико-машиностроительного института Уральского федерального университета, профессор кафедры информационных технологий и автоматизации проектирования, г. Екатеринбург.
Работа поступила в редакцию 26.10.2012.
Библиографическая ссылка
Крючков Д.И., Залазинский А.Г. Моделирование и выбор оптимальной формы матрицы на основе оценки поврежденности для прессования биметаллических проводников // Фундаментальные исследования. – 2012. – № 11-3. – С. 619-624;URL: https://fundamental-research.ru/ru/article/view?id=30584 (дата обращения: 23.11.2024).