Статья посвящена исследованию температурного режима в процессе нагрева неоднородной среды, состоящей из термоэлектрического нагревателя (ТЭН), помещенного в стальную цилиндрическую трубу, песка, которым заполнено пространство между внутренней стальной трубой и внешней медной трубой, и воздуха, которым окружена внешняя труба. Данное исследование актуально для исследований, описанных в статьях
[3, 2] по разработке компьютерной виртуальной модели процесса нагрева неоднородной среды с целью наглядной демонстрации процесса нагрева за небольшой промежуток времени, а также для расчета соответствующих тепловых характеристик на основе реальных экспериментальных данных.
С целью расчета температурного режима в процессе нагрева неоднородной среды «ТЭН-песок-воздух» были проведены три эксперимента с различными электрическими мощностями ТЭН и были произведены замеры температуры с помощью термопары в четырех точках (на поверхности внешней и внутренней труб и в двух внутренних точках) в последовательные моменты времени (через каждые 5 миллисекунд) от начала процесса до момента стабилизации температуры. Показания термопары фиксировались аналого-цифровым преобразователем и обрабатывались компьютерной программой Table Curve 2D. Программа для каждой точки замера выводила свой вариант формулы зависимости температуры от времени (рисунок) с конкретными значениями коэффициентов.
При этом возникают следующие вопросы:
1. Как связаны между собой коэффициенты получаемых формул и тепловые характеристики процесса – коэффициенты теплопроводности, теплоемкости, теплопередачи?
2. Можно ли находить коэффициенты теплопередачи от ТЭНа к песку и теплоотдачи песка воздуху?
3. Какова динамика температуры в пространстве и во времени?
Для ответа на эти вопросы используется методология работы [1], состоящая из следующих этапов:
I. Построение математической модели процесса нагрева в виде начально-краевой задачи для уравнения теплопроводности с краевыми условиями, учитывающими неоднородность среды.
II. Решение краевой задачи методом разделения переменных, где необходимо построить базис собственных функций, удовлетворяющих краевым ус-
ловиям.
III. Расчет тепловых характеристик процесса на основе экспериментальных данных посредством формул стационарного и регулярного режимов.
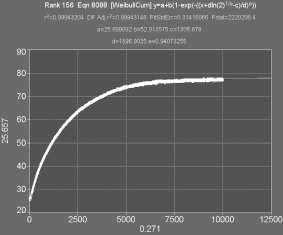
Зависимость температуры от времени и вариант формулы этой зависимости
в программе Table Curve 2D
Исследуемый процесс нагрева «ТЭН-песок-воздух» качественно отличается от процесса, рассмотренного в работе [1]. Вследствие этого получается другая начально-краевая задача, где базис собственных функций явно находить невозможно. Существование и полнота собственных функций соответствующей задачи Штурма-Лиувилля доказаны в работе [4]. С их помощью выводится формула решения начально-краевой задачи, и, в частности, формула регулярного режима. Регулярным режимом определяется «кривая разгона» – кривая изменения температуры от начала процесса нагрева до момента стабилизации.
Построение математической модели
Для построения математической модели процесса нагрева неоднородной среды «ТЭН-песок-воздух» приведем следующие предположения и обозначения.
1. Температура есть функция U(t, x) переменных t и x, где t – время, t ≥ 0, x –
расстояние от центра внутренней трубы до точки, где измеряется температура, r ≤ x ≤ R, r > 0, r – радиус внутренней трубы, R – радиус внешней трубы; в проведенных экспериментах r = 10 мм, R = 50 мм. Следовательно, температура зависит лишь от расстояния до центра внутренней трубы и она постоянна вдоль любой цилиндрической поверхности, концентрично расположенной относительно внутренней трубы.
2. Обозначим через U(t, r) температуру на поверхности внутренней трубы в момент времени t, U(t, r + 0) – температуру песка на границе с внутренней трубой, U(t, x) – температуру песка во внутренней точке x, r < x< R, U(t, R – 0) – температуру песка на границе с внешней трубой, U(t, R) – температуру воздуха вблизи внешней трубы. При этом температурой медной трубы пренебрегаем из-за большого значения коэффициента теплопроводности меди.
3. Неоднородная среда характеризуется следующими константами: cr – удельная теплоемкость внутренней (стальной) трубы, cR – удельная теплоемкость внешней (медной) трубы, Q – количество тепла, выделяющееся из единичной площади внутренней трубы за единичный промежуток времени, hr – коэффициент теплопередачи от внутренней трубы к песку, h – коэффициент теплоотдачи песка воздуху, αR – коэффициент теплопотери воздуха вблизи внешней трубы, k, ρ, c – коэффициент теплопроводности, плотность и удельная теплоемкость песка, 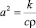 – коэффициент температуропроводности песка.
– коэффициент температуропроводности песка.
Математическая модель процесса нагрева будет состоять из уравнений баланса во внутреннем пространстве песка, на внутренней поверхности трубы, на границах «ТЭН-песок», «песок-воздух», в воздухе вблизи внешней трубы.
Уравнение теплового баланса во внутреннем пространстве песка, согласно закону Фурье, [1], имеет вид:
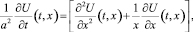 t > 0, r < x < R, (1)
t > 0, r < x < R, (1)
где правая часть есть оператор Лапласа в полярной системе координат с радиус-вектором х.
На поверхности внутренней трубы тепловой баланс зададим условием
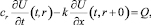 t > 0, (2)
t > 0, (2)
где 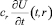 – количество тепла на нагревание внутренней трубы;
– количество тепла на нагревание внутренней трубы; 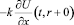 – количество тепла, отдаваемое песку.
– количество тепла, отдаваемое песку.
На границе «ТЭН-песок» условие теплового баланса имеет вид:
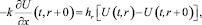 t > 0. (3)
t > 0. (3)
А на границе «песок-воздух» имеем:
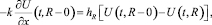 t > 0. (4)
t > 0. (4)
Тепловой баланс в воздухе вблизи внешней трубы зададим условием
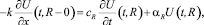 (5)
(5)
где 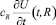 – количество тепла на нагревание внешней трубы; αRU(t, R) – количество тепла, теряемое воздухом вблизи внешней трубы.
– количество тепла на нагревание внешней трубы; αRU(t, R) – количество тепла, теряемое воздухом вблизи внешней трубы.
В начальный момент неоднородная среда имеет температуру окружающей среды:
U(0, x) = u0, r ≤ x ≤ R. (6)
Таким образом, математическая модель процесса нагрева представляет собой начально-краевую задачу для дифференциального уравнения теплопроводности (1) в полярной системе координат с краевыми условиями (2), (3) – на внутренней границе, (4), (5) – на внешней границе, и начальным условием (6). Решением U(t, x), t ≥ 0, r ≤ x ≤ R начально-краевой задачи (1)–(6) определяется температурный режим в процессе нагрева неоднородной среды «ТЭН-песок-воздух». Функция U(t, x) при каждом t > 0 терпит разрыв в точках x = r и x = R .
Стационарный режим
Стационарным режимом, как в работе [1], называем стабилизацию температуры в процессе нагрева:
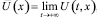 r ≤ x ≤ R,
r ≤ x ≤ R,
где 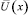 – температура на расстоянии x от центра ТЭНа при стабилизации. В формулах (1)‒(5), переходя к пределу при t → +∞, выводим, что функция
– температура на расстоянии x от центра ТЭНа при стабилизации. В формулах (1)‒(5), переходя к пределу при t → +∞, выводим, что функция 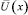 должна удовлетворять следующим условиям:
должна удовлетворять следующим условиям:
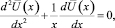 r < x < R,
r < x < R,
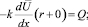
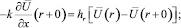
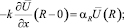
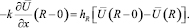
Отсюда находим 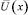 :
:
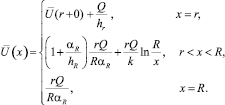 (7)
(7)
По формуле (7) на основе экспериментальных данных можно находить значения тепловых констант αR, k, hr, hR. А именно, пусть известны значения температуры в четырех точках замера при стабилизации:
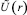 ,
, 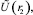
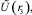 ,
, 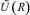
где r < r2 < r3 < R. Полагая
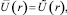 ,
,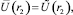
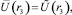
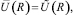
относительно неизвестных αR, k, hr, hR, получим следующую систему линейных урав-
нений:
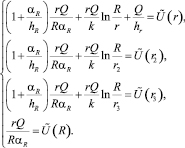
Находим неизвестные:
 (8)
(8)
Решение начально-краевой задачи
Решение задачи (1)–(6) находим в следующем виде:
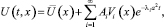 (9)
(9)
где числа 0 < λ1 < λ2 < ... < λn < ... и функции определяются как собственные значения и собственные функции задачи Штурма-Лиувилля в форме Кнезера [1]:
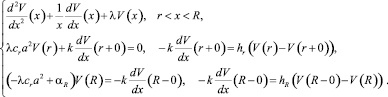 (10)
(10)
В работе [4] доказаны существование и полнота собственных функций задачи (10) в пространстве функций

со скалярным произведением
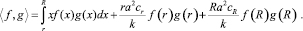
Другими словами, любая функция f(x) ∈ H единственным образом представима в виде ряда по собственным функциям задачи (10):
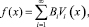
где Bi = ⟨f, Vi⟩, ⟨Vi, Vi⟩ = 1, i = 1, 2, ...
и ⟨Vi, Vj⟩ = 0 при i ≠ j. При этом для первого собственного значения λ1 имеет место неравенство:
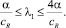
Полагая 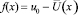 , находим
, находим
коэффициенты Ai, i = 1, 2, ... представ-
ления (9):
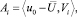 i = 1, 2, ... . (11)
i = 1, 2, ... . (11)
В этом случае ряд в правой части формулы (9) при каждом t > 0 сходится в обычном смысле.
Регулярный режим
Согласно терминологии работы [5], регулярный температурный режим определяется приближенной формулой
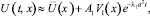
где λ1 – первое собственное значение, а V1(x) – соответствующая нормированная собственная функция задачи Штурма-Лиувилля (10); их можно находить приближенно численно-аналитическими методами. Коэффициент A1 определяется формулой
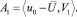
Таким образом, можно задать следующий алгоритм расчета регулярного температурного режима в процессе нагрева неоднородной среды «ТЭН-песок-воздух»:
1. По экспериментальным данным 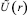 ,
, 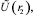 ,
, 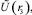 ,
, 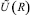 , полученным в ходе замеров температуры в четырех точках при стабилизации, находим приближенные значения тепловых констант с помощью формул (8).
, полученным в ходе замеров температуры в четырех точках при стабилизации, находим приближенные значения тепловых констант с помощью формул (8).
2. Численно-аналитическими методами находим приближенные значения первого собственного значения λ1 задачи Штурма-Лиувилля (10) и соответствующей нормированной собственной функции V1(x).
3. Находим стационарный режим 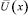 формулой (7).
формулой (7).
4. Вычисляем коэффициент A1 формулой
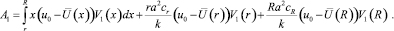
5. Регулярный режим рассчитывается формулой
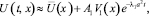 r ≤ x ≤ R , t ≥ 0. (12)
r ≤ x ≤ R , t ≥ 0. (12)
Рецензенты:
Горбунов В.А., д.ф.-м.н., профессор, главный специалист ООО НПФ «ЭнергоКИТ», г. Вологда;
Калягин Ю.А., д.т.н., профессор, главный конструктор Общества с ограниченной ответственностью Научно-производственный центр «Информационные и энергетические технологии» (ООО НПЦ «Инэнтех»), г. Вологда.
Работа поступила в редакцию 16.10.2012.
Библиографическая ссылка
Телков М.Г., Тимошенко П.О., Суханов И.А., Наимов А.Н., Синицын А.А. ИССЛЕДОВАНИЕ ТЕМПЕРАТУРНОГО РЕЖИМА В ПРОЦЕССЕ НАГРЕВА НЕОДНОРОДНОЙ СРЕДЫ «ТЭН-ПЕСОК-ВОЗДУХ» // Фундаментальные исследования. 2012. № 11-2. С. 458-462;URL: https://fundamental-research.ru/ru/article/view?id=30558 (дата обращения: 12.03.2026).



