В связи с тем, что в настоящее время наблюдается тенденция к постоянному увеличению объемов информационного обмена, ширина используемой для этого полосы спектра в каналах также постоянно увеличивается. Это характерно для систем передачи информации различного вида и назначения. Некоторые из них используют каналы, которым по их природе присуща многолучевость, т.е. передача сигналов от передатчика к приемнику по нескольким путям с различной временной задержкой. Если при этом в цифровых системах передачи разброс времен задержки распространения по различным лучам значительно превышает длительность отдельных символов, то возможно появление межсимвольной интерференции (МСИ) из-за взаимного наложения соседних символов, вызывающего значительные искажения [1, 2]. Известны различные методы, позволяющие снизить негативные последствия МСИ. Одним из перспективных является метод, использующий определенное сходство между сверточным кодированием и воздействием МСИ.
Действительно, после согласованной фильтрации и детектирования в приемнике каждый принятый символ yi равен сумме нескольких (m) переданных символов xi, взятых с определенными весовыми коэффициентами ai, которые определяются структурой многолучевого канала [1, 3, 4], т.е.:
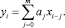
При осуществлении сверточного кодирования исходный поток символов преобразуется в новый поток с увеличенным числом символов, в котором каждый символ является логической функцией определенного числа символов исходного потока и вносится избыточность, определяющаяся соотношением количества исходных информационных символов и символов после кодирования. Декодирование возможно различными способами, из которых для целей борьбы с МСИ возможно после модификации использовать подход, реализуемый при «мягком» декодировании Витерби [1]. Это обусловлено следующим.
Воздействие МСИ на сигналы сходно с определенного рода «естественным» кодированием. Как при сверточном кодировании, так и при межсимвольной интерференции каждый символ является функцией нескольких предыдущих символов исходного потока. Различия наблюдаются в том, что при сверточном кодировании каждый новый символ является результатом логических операций над исходными символами, т.е. получается применением логической функции. А при МСИ каждый принятый символ получается весовым арифметическим суммированием нескольких предыдущих символов исходной последовательности т.е. получается путем применения арифметической функции.
Кроме того, сверточное кодирование предполагает введение избыточности. Если же рассматривать воздействие МСИ, как некоторый вариант «арифметического» кодирования, то здесь избыточность отсутствует. Однако сходство основных принципов преобразования исходного потока символов в новый поток позволяет применить для декодирования методы, применяемые для сверточных кодов. В этом случае осуществление декодирования в применении к передаче через многолучевые каналы будет означать устранение влияния МСИ.
Возможна реализация метода в «слепом» варианте и в варианте с применением тестовых сигналов. Слепой вариант осуществляется предварительной оценкой коэффициентов aj на основе внутренних связей между символами и требует заметно большего времени для обработки цифровой последовательности. Если возможно применение тестовых сигналов, периодически передаваемых по каналу в специально отведенные промежутки времени, то коэффициенты aj определяются простым измерением.
Модификация «мягкого» алгоритма Витерби [3, 4, 5] заключается в том, что, если раньше при использовании решетчатой диаграммы состояний и переходов каждая ветвь решетки обозначала прием нескольких символов, в модифицированном методе каждая ветвь перехода из конкретного состояния («кодового слова») в другое состояние обозначает прием одного текущего символа.
При «жестком» декодировании сверточных кодов метрики расстояний от всех вариантов переходов по решетке на каждом шаге определяются, как расстояния Хэмминга и имеют целочисленные значения. При «мягком» декодировании веса переходов между состояниями также принимают целочисленные значения, а отсчеты сигнала могут уже принимать дробные значения и метрики – это уже «арифметические» расстояния. В описываемом варианте сверточной процедуры и отсчеты сигнала, и веса переходов имеют дробные значения. Метрики переходов на каждом шаге определяются, как расстояния между принятым значением текущего символа и вариантами алгебраической суммы коэффициентов aj, взятых со всеми возможными сочетаниями знаков.
Отдельного рассмотрения требует метод определения соответствующих метрик. Действительно, при известных вариантах реализации «мягкого» алгоритма Витерби метрики определяются, как модули разности между значением принятого сигнала и всеми возможными его реализациями. Для каждого пути по решетке определяется сумма метрик переходов, составляющих этот путь. При приеме каждого нового символа один из двух возможных путей, подходящих к каждому возможному варианту символа, откидывается после сравнения их суммарных метрик. Количество оставшихся путей постоянно уменьшается, пока не остается только один, и на его основе принимаются решения о значениях переданных символов. Суммарная метрика пропорциональна сумме линейных расстояний между принятым сигналом и его вариантами. Однако эффективность обработки можно увеличить, если использовать нелинейные метрики.
Рассмотрим подход, предложенный Омурой [6], который показал, что алгоритм Витерби реализует оценку по максимуму правдоподобия. Действительно, на текущем шаге i оцениваются пути с разными суммарными метриками. Каждый из путей соответствует определенной k-й последовательности принятых символов {xi}(k). Если бы отсутствовал тепловой шум, то, зная коэффициенты aj, можно было бы точно определить путь с минимальной суммарной метрикой, а значит и восстановить передаваемую цифровую последовательность. Однако из-за наличия шума сравнение метрик путей носит вероятностный характер, необходимо сравнивать условные вероятности каждого варианта пути при приеме последовательности {yi}, т.е. величины 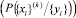 .
.
Поскольку символы передаваемой информационной последовательности могут считаться независимыми, то каждую такую условную вероятность можно представить в виде произведения:
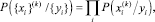 (1)
(1)
верхний индекс в скобках здесь также обозначает принадлежность к k-тому варианту пути; произведение берется по необходимому количеству номеров i предыдущих символов.
Как известно, для сравнения можно при необходимости использовать не сами величины, а монотонные функции от них, в частности, для случая гауссова распределения теплового шума удобной функцией является логарифм. В этом случае выражение (1) превращается с сумму квадратичных форм:
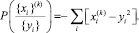 (2)
(2)
Таким образом, путь с максимальным правдоподобием соответствует минимальной сумме из правой части (2). А это – сумма метрик, равных квадратам расстояний между принятым сигналом и его вариантами, а не модулей этих расстояний, как принято в стандартных реализациях алгоритмов «мягкого» декодирования Витерби. Использование квадратичной метрики вместо линейной может дать выигрыш по помехоустойчивости.
Для оценки величины выигрыша от применения квадратичной метрики была проведена серия модельных компьютерных экспериментов. Информационный сигнал имитировался последовательностью случайных равновероятных бинарных отсчетов. Структура МСИ определялась наборами из трех (m = 3) коэффициентов, значения которых могли выбираться произвольными. Воздействие теплового шума имитировалось случайными гауссово распределенными отсчетами. Мощность шума задавалась по отношению к мощности полезного сигнала выбором различной величины отношения «сигнал/шум» (в дБ). Мощность сигнала оценивалась не по мощности основного компонента (a1), а по суммарной мощности всех трех полезных компонент (т.е. пропорционально величине 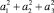 ).
).
Моделирование работы подобного алгоритма показало его достаточно высокую эффективность. Некоторые результаты моделирования представлены на графиках, рис. 1 и 2.
На графиках рис. 1, приведены зависимости вероятности ошибки РВ при передаче двоичного сигнала от отношения «сигнал/шум» ρ при одновременном воздействии межсимвольной интерференции. Из результатов моделирования показаны характерные зависимости, в частности, для наборов коэффициентов: а1 = 1, а2 = 0,8, а3 = 0,3 – графики 1; а1 = 1, а2 = 1, а3 = 1 – графики 2; а1 = 0,3, а2 = 0,6, а3 = –0,4. Сплошные линии графиков соответствуют построению линейных метрик, прерывистые линии графиков соответствуют построению квадратичных метрик. Для сравнения графики для линейных и квадратичных метрик рассчитывались для одинаковых условий работы. График, обозначенный на рис. 1 номером 4, соответствует случаю, когда при воздействии МСИ обработка по борьбе с ними не проводилась. Этот график имеет одинаковый вид для любых сочетаний параметров а1, а2, а3 и может быть отнесен ко всем трем ситуациям.
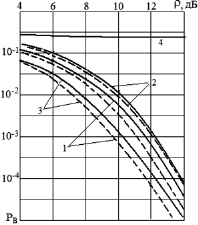
Рис. 1. Сравнительная помехоустойчивость метода сверточной обработки при линейной и квадратичной метриках
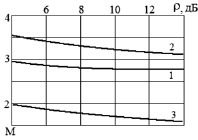
Рис. 2. Средняя задержка
восстановления сигнала
Как известно, при использовании классического алгоритма Витерби окончательный вариант декодированной последовательности формируется с некоторым запаздыванием на М символов относительно текущего обрабатываемого символа. Причем М – случайная переменная величина. В описываемом модифицированном алгоритме восстановление передаваемой битовой последовательности также происходит с некоторой задержкой на М символов.
При моделировании контролировалось это количество символов в зависимости от отношения «сигнал/шум» при различных сочетаниях параметров. Графики на рис. 2 показывают среднее по выборке количество М в зависимости от отношения для тех же наборов параметров, что и на рис. 1.
По результатам моделирования можно сделать следующие выводы.
1. При значительном уровне межсимвольной интерференции происходит столь значительное снижение помехоустойчивости, что без применения специальных мер передача информации становится невозможной.
2. Применение описанного метода борьбы с межсимвольной интерференцией с помощью сверточных процедур позволяет значительно увеличить помехоустойчивость и качество передачи сигналов, доведя его до достаточно высокого уровня.
3. Использование квадратичных метрик в сверточной процедуре дает возможность улучшить помехоустойчивость до 0,5 дБ.
4. Выигрыш от применения модифицированного алгоритма и квадратичных метрик зависит от сочетания параметров межсимвольной интерференции.
5. Задержка восстановления передаваемой последовательности символов мало зависит от отношения «сигнал/шум» и заметно зависит от сочетания параметров МСИ.
Рецензенты:
Смирнов А.А., д.т.н., доцент, профессор кафедры высшей алгебры и геометрии, ГОУ ВПО «Ставропольский государственный университет (СГУ)», г. Ставрополь;
Червяков Н.И., д.т.н., профессор, заведующий кафедрой прикладной математики и информатики ГОУ ВПО «Ставропольский государственный университет (СГУ)»,
г. Ставрополь.
Работа поступила в редакцию 16.10.2012.
Библиографическая ссылка
Никитин О.Р., Полушин П.А., Ульянова Е.В., Синицын Д.В. МЕТРИКА ПРИ СВЕРТОЧНОЙ ОБРАБОТКЕ ЦИФРОВЫХ СИГНАЛОВ // Фундаментальные исследования. 2012. № 11-2. С. 450-453;URL: https://fundamental-research.ru/ru/article/view?id=30556 (дата обращения: 12.03.2026).



